Причины ложных результатов регрессионного анализа

Часто при работе с выборками данных не все процедуры регрессионного анализа проходят гладко и дают результаты, пригодные для практического использования.

Рассмотрим некоторые проблемы регрессионного анализа реальных данных, причины их возникновения и возможные пути преодоления:

1. Грубое искажение вида модели или оценок ее параметров

1) Проблема может возникнуть из-за неоднородности исходных данных, наличия, так называемых, аномальных наблюдений (выбросов). Например, на рисунке 1 одна единственная, последняя, точка показала смену тенденции, и результатом моделирования стала парабола.

Рис. 1. Эффект выбросов

Чтобы устранить эффект выбросов надо провести тщательный предварительный анализ данных и, возможно, даже удалить эти точки из анализируемой совокупности.

Иногда для достижения однородности данных используют их преобразования и переход к производным переменным.

2) К названной проблеме могут привести ошибки выборки данных. Выборка может быть, например, недостаточной длины. При увеличении же объема выборки необходимо помнить, что все используемые данные должны быть сформированы в одних и тех же условиях.

3) Регрессионный анализ пойдет по ложному пути и в случае ошибок измерений.

2. Несоответствие результатов корреляционного и регрессионного анализа

Проблема заключается в том, что корреляционный анализ, например, показывает прямую связь между переменными, а коэффициент регрессии 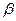в линейной модели регрессии отрицательный.

Причины здесь, очевидно, в неправильном выборе фактора для исследования интересующей нас переменной или в несоответствии вида модели. Таким образом, при возникновении такой проблемы следует изменить спецификацию модели.

3. Отрицательные расчетные значения эндогенной переменной

В этом случае нужно либо изменить метод оценивания параметров модели, либо изменить ее спецификацию.

4. Интервал прогноза с отрицательной нижней границей или слишком широкий

Если модель обладает хорошим качеством, то достаточно изменить вероятность оценки ошибки прогнозирования U.

5. Эффект ложной регрессии

Большинство финансово-экономических показателей являются нестационарными (рис. 2).

Рис. 2. Пример нестационарных данных

К нестационарным данным, вообще говоря, нельзя применять обычные процедуры статистического анализа, в том числе и регрессионного. Полученные в этом случае регрессии могут быть ложными.

Работа с нестационарными данными – это предмет отдельного разговора, выходящий за рамки нашего курса. Отметим лишь, что применение корреляционно-регрессионного анализа к нестационарным данным возможно, когда переменные имеют схожие тенденции в течение длительного промежутка времени (рис. 2)[9].

Рис. 2. Временные ряды с похожими тенденциями

Заключительные замечания для преподавателей

1) Тривиальность данных в примерах обусловлена намерением преподавателя показать все тонкости рассматриваемых эконометрических процедур без лишних проблем, связанных с особенностями реальных данных. Работу с реальными данными целесообразно продемонстрировать в начале практического занятии на ПЭВМ.

2) Количество презентаций на одной лекции не должно превышать 9-10. В противном случае студенты получат не наглядное изложение материала, а мелькание картинок, отвлекающее внимание и раздражающее психику.

[1] Именно в такой интерпретации студенты изучали данный материал в названных выше курсах. Далее в лекции процедура оценки параметров линейной модели рассматривается в несколько иной интерпретации, наиболее приближенной к языку эконометрики.

[2] В справедливости формул для оценки параметров, представленных через отклонения , студентам рекомендуется убедиться самостоятельно.

[3] Этот материал рассматривается более подробно в студенческих группах с хорошей математической подготовкой (реализуется дифференцированный подход).

[4] Здесь приведено несколько интерпретаций понятия «число степеней свободы». Это элементы методики вариативного изложения материала. Они будут использоваться в лекции и далее.

[5] Реализуются междисциплинарные и межпредметные связи.

[6] Используется методика вариативного изложения материала.

[7] Опережающее обучение.

[8] Этот материал можно рекомендовать отдельным студентам для более углубленного изучения с последующим представлением результатов работы в виде реферата.

[9] Явление совпадения тенденций переменных в течение длительного промежутка времени называется коинтеграцией. За разработку метода коинтеграции американский ученый Роберт Ингл и британский экономист Клайв Грэнджер в 2003 г. получили премию Альфреда Нобеля.