Общие сведения о регрессионном анализе

Пример

Пусть зависимая переменная Y – квартальная прибыль девяти компаний одной отрасли (в млн. руб.), а фактор X – объем продаж товара этих компаний за квартал (в тыс. шт.). Исходные данные представлены в таблице 1.

Таблица 1

№ п.п.	Y	X

Решение:

1) найти параметры уравнения линейной регрессии, дать экономическую интерпретацию коэффициента регрессии

Диаграмма рассеяния (рис. 4) демонстрирует наличие прямой и достаточно тесной связи переменных.

Рис. 4. Диаграмма рассеяния исходных данных

Для решения задачи построим расчетную таблицу 2:

№ п.п.	Yi	X	X-Xcp	(X-Хcp)^2	Y-Ycp	(X-Xcp)*(Y-Ycp)	Yip	ei
			-9		-31		31.65	-6.65
			-7		-22		37.07	-3.07
			-4		-14		45.2	-3.2
			-6		-5		39.78	11.22
					-1		56.04	-1.04
							64.17	2.83
							75.01	-2.01
							69.59	6.41
							85.85	-4.85
Сумма								-0.36
Среднее

Таблица 2

Уравнение регрессии:

Y_i=-90.3 + 2.71*X_i + е_i,

при этом

Y_iр=-90.3 + 2.71*X_i .

Предпоследний столбец в таблице 1 получен в результате подстановки в модель регрессии фактических значений фактора. Последний столбец представляет ошибки моделирования .

Экономический смысл коэффициента регрессии:

при изменении объема продаж компании (Х) на 1 тысячу штук прибыль (Y) будет меняться в ту же сторону на 2,71 млн. руб.

Результат моделирования представлен на рисунке 5.

Рис. 5. Результаты приближения фактических значений прибыли линией регрессии

Замечание.

Уравнение регрессии и целый ряд его характеристик (в т.ч. (Предсказанное Y) и (Остатки)) можно получить, воспользовавшись инструментом Регрессия в пакете Анализ данных в Excel (таблицы 3, 4).

Таблица 3

	Коэффициенты
Y-пересечение	-90.33160622
X	2.70984456

Таблица 4

Наблюдение	Предсказанное Y	Остатки
	31.61	-6.61
	37.03	-3.03
	45.16	-3.16
	39.74	11.26
	56.00	-1.00
	64.13	2.87
	74.97	-1.97
	69.55	6.45
	85.81	-4.81

■

Анализ вариации зависимой переменной в уравнении регрессии[3]

Особую роль в эконометрических исследованиях играют различные виды дисперсий (вариаций). Дисперсия – это величина, характеризующая степень отклонения (разброса, рассеяния) каких-либо величин друг относительно друга. В зависимости от величин рассматривают разные дисперсии.

Рассмотрим вариацию (дисперсию, разброс) значений зависимой переменной Y вокруг их среднего значения .

Разобьем отклонения на две части

.

Тогда дисперсия Y представляется в виде трех слагаемых

.

Можно показать (самостоятельно), что третье слагаемое в этом равенстве равно нулю. Таким образом,

. (3)

Пояснения к формуле (3)

1. TSS = – общая сумма квадратов отклонений (общая дисперсия), которая характеризует степень разброса фактических значений исследуемой переменной Y около их среднего значения (рис.6);

Рис. 6. Общая сумма квадратов отклонений

1. RSS = – сумма квадратов отклонений, объясненная регрессией (факторная дисперсия), характеризует степень отклонения расчетных значений исследуемой переменной от среднего значения (рис.7);

Рис. 7. Объясненная (факторная) сумма квадратов отклонений

2. ESS = – остаточная сумма квадратов отклонений (остаточная дисперсия), оценивает степень отклонения линии регрессии от фактических значений исследуемого показателя (рис.8).

Рис. 8. Остаточная сумма квадратов отклонений

Любая сумма квадратов отклонений связана с числом степеней свободы, т.е. числом свободы независимого варьирования признака. Число степеней свободы равно разности между числом независимых наблюдений случайной величины n и числом связей, ограничивающих свободу их изменения. Число степеней свободы связано с числом единиц совокупности n и с числом определяемых по ней констант. Число степеней свободы должно показать, сколько независимых отклонений из n возможных требуется для образования данной суммы квадратов[4].

Для общей суммы квадратов TSS = необходимо (n-1) независимых отклонений, т.к. по совокупности из n единиц после расчета среднего уровня свободно варьируют лишь (n-1) отклонение.

Факторная сумма квадратов RSS = при линейной регрессии зависит только от одной константы – коэффициента регрессии 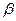. Поэтому данная сумма имеет одну степень свободы.

Подобно равенству (3), можно установить равенство между числом степеней свободы соответствующих сумм квадратов

,

из которого видно, что число степеней свободы остаточной суммы квадратов при линейной регрессии составляет (n-2). Действительно, две степени свободы теряются при определении двух параметров регрессии из системы нормальных уравнений.

Разделив каждую сумму квадратов на соответствующее ей число степеней свободы, получим средний квадрат отклонений или дисперсию на одну степень свободы:

,

,

.

Дисперсии на одну степень свободы приводят различные дисперсии к сравнимому виду.

Замечание

Различные суммы квадратов отклонений, число степеней свободы и дисперсии на одну степень свободы можно получить в отчете по регрессионному анализу (таблица Дисперсионный анализ). Соответствующие результаты по данным нашего примера приведены в таблице 5.

Таблица 5

Дисперсионный анализ
	df	SS	MS
Регрессия		2834.50	2834.50
Остаток		267.50	38.21
Итого		3102.00

Пояснения к таблице

1. Столбец df – число степеней свободы.

2. Столбец SS – суммы квадратов, соответственно факторная, остаточная, общая.

3. Столбец MS – дисперсии на одну степень свободы, соответственно факторная и остаточная.

Проверка качества модели

В задачу регрессионного анализа входит не только построение самой модели, но и исследование ее соответствия реальным (фактическим) данным.

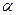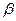Оценки и параметров регрессионного уравнениядолжны обладать определенными свойствами. Они должны быть несмещенными, состоятельными и эффективными.

Несмещенность оценок означает, что математическое ожидание остатков равно 0.

Оценки считаютсяэффективными, если они характеризуются наименьшей дисперсией.

Состоятельность оценок характеризует увеличение их точности с увеличением объема выборки.

Указанные критерии оценок (несмещенность, состоятельность и эффективность) обязательно учитываются при разных способах оценивания. МНК строит оценки регрессии на основе минимизации суммы квадратов остатков. Поэтому для проверки названных критериев важно исследовать поведение остаточных величин регрессии. Условия, необходимые для получения несмещенных, состоятельных и эффективных оценок, представляют собойпредпосылки МНК, соблюдение которых желательно для получения достоверных результатов регрессии.

Исследования остатков предполагают проверку наличия следующих пяти предпосылок МНК:

1) случайный характер остатков;

2) независимость остатков или отсутствие их автокорреляции;

3) остатки подчиняются нормальному распределению;

4) нулевая средняя величина остатков (или их математическое ожидание), не зависящая от уровней фактора Х;

5) гомоскедастичность остатков – дисперсия каждого отклонения одинакова для всех значений фактора.

Теорема Гаусса-Маркова.Если регрессионная модель 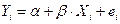удовлетворяет предпосылкам1, 2, 4, 5,то оценк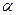и и 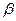имеют наименьшую дисперсию в классе всех линейных несмещенных оценок.

Выполнение предпосылки 3 (нормальность распределения остатков) позволяет использовать критерии t и F (см. ниже)при анализе свойств модели и ее параметров.

Проверка первых четырех предпосылок представляет собой исследование адекватности модели определенным статистическим критериям. Этот материал подробно рассмотрен в курсе ЭММиПМ в теме «Моделирование и прогнозирование временных рядов»[5].

Рассмотрим подробнее исследование гомоскедастичности остатков. Остатки считаются гомоскедастичными, если для каждого значения фактора они имеют одинаковую дисперсию. Иными словами остатки распределены вдоль оси абсцисс случайно с одинаковой частотой и амплитудой. В этом случае на графике остатков они расположены в виде достаточно узкой горизонтальной полосы[6] (рис.9).

Рис. 9. Гомоскедастичные остатки

Если это условие не соблюдается, то имеет место гетероскедастичность остатков. Гетероскедастичные остатки имеют направленность в своем распределении (рис. 10).

Рис. 10. Гетероскедастичные остатки

При малом объеме выборки для оценки гетероскедастичности может использоваться метод Гольдфельда – Квандта, разработанный в 1965 году. Тест, предложенный этими учеными, включает в себя следующие шаги:

1. Упорядочение n наблюдений по мере возрастания переменной X.

2. Исключение из рассмотрения С центральных наблюдений; при этом (n-C):2>p, где р – число оцениваемых параметров ( ).

3. Разделение совокупности из (n-C) наблюдений на две группы (соответственно с малыми и большими значениями фактора Х) и определение по каждой из групп уравнений регрессии.

4. Определение остаточной суммы квадратов для первой (S1) и второй (S2) групп и нахождение их отношения: R=S1:S2 (в числителе должна стоять большая величина).

Вывод о гомоскедастичности делается с помощью F-критерия Фишера с (n-C-2p):2 (р – число оцениваемых в уравнении параметров; для парной регрессии р=2) степенями свободы для каждой остаточной суммы квадратов. Чем больше величина R превышает табличное значение F-критерия, тем более нарушена предпосылка о равенстве дисперсий остаточных величин.

Замечание

Табличное значение F-критерия можно найти с помощью статистической функции FРАСПОБР.

Протестируем данные нашего примера на наличие гомоскедастичности остатков.

Пример (продолжение).

2) проверить выполнение предпосылок МНК:

Проверку предпосылок 1 – 4 выполнить самостоятельно, используя материал дисциплины ЭММиПМ.

Проверка предпосылки 5:

1. Упорядочим переменную Y по возрастанию фактора Х (в Excel для этого можно использовать команду Данные – Сортировка – По возрастанию Х).

Исходные данные

Y	X

Упорядоченные данные

Y	X

2. Уберем из середины упорядоченной совокупности С=1/4*n=1/4*9 2 значения. В результате получим две совокупности по ½*(9-2)=4 значения соответственно с малыми и большими значениями Х.

3. Для каждой совокупности в отдельности выполним регрессионный анализ (рисунок 11).

Для первой совокупности:

Дисперсионный анализ
	df	SS	MS
Регрессия		200.0769	200.0769
Остаток		169.9231	84.96154
Итого

Для второй совокупности:

Дисперсионный анализ
	df	SS	MS
Регрессия		78.75	78.75
Остаток
Итого		102.75

Рис. 11.Фрагменты регрессионного анализа для первой и второй совокупностей соответственно

4. Найдем отношение полученных остаточных сумм квадратов (в числителе должна быть большая сумма):

R= 169,9/24 =

7.08

5. Вывод о наличии гомоскедастичности остатков делаем с помощью F-критерия Фишера с уровнем значимости и двумя одинаковыми степенями свободы:

Число степеней свободы:	(9-1-2*2):2=2
Fтаб(0,05;2;2)=

Так как , то обнаруживается наличие гомоскедастичности в остатках модели по отношению к фактору Х.

■

Замечание

При нарушении гомоскедастичности остатков модели и наличии автокорреляции в них рекомендуется заменять традиционный МНК обобщенным МНК (ОМНК), в основе которого лежит работа с предварительно преобразованными исходными данными[7].

Для анализа качества регрессионных моделей используется ряд дополнительных специфических характеристик. К ним относится, например, индекс корреляции:

.

Этот коэффициент является универсальным, так как отражает тесноту связи и точность модели, может использоваться при любой форме связи переменных. Для парной линейной модели индекс корреляции равен коэффициенту парной корреляции, т.е.

.

На практике чаще используется его квадрат, который называется коэффициентом детерминации:

.

, иногда выражают не в долях, а в процентах.

Коэффициент детерминации показывает,какая доля вариации (случайных колебаний, общей дисперсии) признака Y учтена в построенной модели и обусловлена случайными колебаниями включенного в нее фактора. Качество модели тем лучше, чем ближе к 1. Иными словами характеризует степень влияния включенных в модель факторов. Влияние факторов, не учтенных в модели, определяется тогда величиной 1- . Модель тем лучше, чем больше и меньше 1- .

Для оценки уровня точности регрессионных моделей используется также средняя относительная ошибка аппроксимации

.

Величина 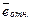показывает, на сколько процентов в среднем фактические значения исследуемой величины отличаются от расчетных. Модель тем точнее, чем меньше 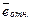. Часто наиболее приемлемыми считают значения .

В качестве меры точности модели применяют также оценку остаточной дисперсии или квадратный корень из нее , называемый стандартной ошибкой модели или среднеквадратическим отклонением.

Точность модели тем лучше, чем меньше ее стандартная ошибка (это же имеет место и при использовании для оценки уровня точности других видов ошибок). Однако, понятие «чем меньше» является относительным и зависит от порядка чисел, представляющих данные задачи. Поэтому модель считается точной, если стандартная ошибка модели меньше стандартной ошибки (среднеквадратического отклонения) результативного признака Y . Стандартную ошибку легко найти в Excel с помощью статистической функции СТАНДОТКЛОН.

Пример (продолжение).

3) вычислить коэффициент детерминации, найти среднюю относительную ошибку аппроксимации, сделать вывод о качестве модели

Необходимые предварительные расчеты представлены в таблице 6.

Таблица 6

№ пп	Y	Y-Yср	e	e^2	eотн	(Y-Yср)^2	X^2
		-31	-6.65	44.22	26.6
		-22	-3.07	9.42	9.03
		-14	-3.2	10.24	7.62
		-5	11.22	125.89
		-1	-1.04	1.08	1.89
			2.83	8.01	4.22
			-2.01	4.04	2.75
			6.41	41.09	8.43
			-4.85	23.52	5.99
Сумма			-0.36	267.52	88.54
Среднее					9.84

;

вывод: 91,4 % случайной вариации исследуемого признака Y (прибыль) учтено в построенной модели и обусловлено случайными колебаниями включенного в нее фактора Х (объем продаж); влияние неучтенных в модели факторов ( ) около 9 %.

вывод: фактические значения прибыли Y отличаются от модельных в среднем на 9.8 %; уровень точности модели достаточный.

Cтандартная ошибка модели 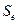и коэффициент детерминации 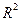выводятся в первой таблице «Регрессионная статистика» отчета по регрессионному анализу. Для нашей модели эта таблица представлена на рисунке 12.

Регрессионная статистика
Множественный R	0.956
R-квадрат	0.914
Нормированный R-квадрат	0.901
Стандартная ошибка	6.182
Наблюдения	9.000

Рисунок 12. Фрагмент регрессионного анализа

В нашем случае стандартная ошибка модели , а среднеквадратическое отклонение (или стандартная ошибка) Y . Так как < , то модель регрессии является точной.

■

Парная нелинейная регрессия

Общий вид регрессионной модели:

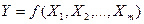. (1)

Если в уравнении (1) присутствует только один фактор X, а f – нелинейная математическая функция, получим парную нелинейную модель регрессии вида

Y=f(X).

Парная линейная регрессия проста в использовании, удобна и наглядна. Но среди реальных экономических данных линейные зависимости встречаются нечасто. Поэтому в эконометрических исследованиях чаще применяются нелинейные модели (рис. 16).

а) гиперболическая функция может использоваться для показателей, достигающих насыщения, начиная с определенных значений фактора (верхняя горизонтальная асимптота);

б) парабола применяется в тех случаях, когда исследуемая величина меняет направление своего развития;

в) затухающие колебания могут характеризовать объемы продаж сезонного товара на этапе ухода с рынка.

Рис. 16. Примеры нелинейных зависимостей

Различают два класса нелинейных регрессий:

1) регрессии, нелинейные относительно объясняющих переменных, но линейные по оцениваемым параметрам;

2) регрессии, нелинейные как относительно объясняющих переменных, так и относительно оцениваемых параметров.

К первому классу относятся, например:

1) полиномы разных степеней

;

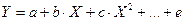2) равносторонняя гипербола

.

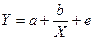Ко второму классу относятся:

1) степенная функция

;

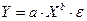2) показательная

;

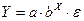3) экспоненциальная

.

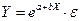Работа с такими моделями сводится к их предварительной линеаризации (приведению к линейному виду). Модели из первого класса приводятся к линейному виду простой заменой переменных. Для линеаризации моделей второго класса используют полулогарифмическую функцию или логарифмирование. Полученные таким образом вспомогательные линейные модели оценивают обычным МНК. Затем осуществляют обратный переход к нелинейной функции.

Замечание.

Если модель второго класса с помощью соответствующих преобразований может быть приведена к линейному виду, то она называется внутренне линейной, если же модель не может быть сведена к линейной функции, то она называется внутренне нелинейной (например, 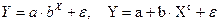и другие). Для оценки параметров таких моделей используются итеративные процедуры.

Кривые Энгеля и Филлипса[8]

Примером использования равносторонней гиперболы 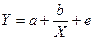являются кривые Филлипса и Энгеля.

Кривая Филлипса показывает взаимное изменение уровней безработицы (х) и инфляции в экономике (или процента прироста заработной платы) (y). Названа по имени английского экономиста А. Филлипса, который впервые представил графики подобного рода в 1958 г. (рис. 17).

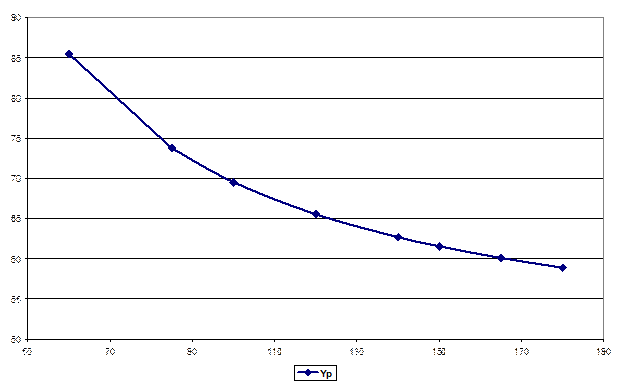
Рис. 17. Кривая Филлипса

Такая форма кривой (обратная зависимость с нижней горизонтальной асимптотой) показывает, что инфляция (или прирост заработной платы) высока при низкой безработице и низка – при высокой. Соответственно можно определить тот уровень безработицы, при котором заработная плата оказывается стабильной и темп ее прироста равен нулю.

Кривая Энгеля показывает величину расходов на товары в зависимости от роста дохода. Эта взаимосвязь была впервые проанализирована в 19 в. немецким статистиком Э. Энгелем. Закон Энгеля устанавливает, что доля расходов на продовольственные товары по мере роста дохода падает, т.к. продукты питания относятся к необходимым товарам. В то же время с увеличением дохода доля расходов на непродовольственные товары будет возрастать. При этом можно определить границу величины дохода, дальнейшее увеличение которого не приводит к росту доли расходов на отдельные непродовольственные товары (имеем медленно повышающуюся функцию с верхней горизонтальной асимптотой, рис. 18).

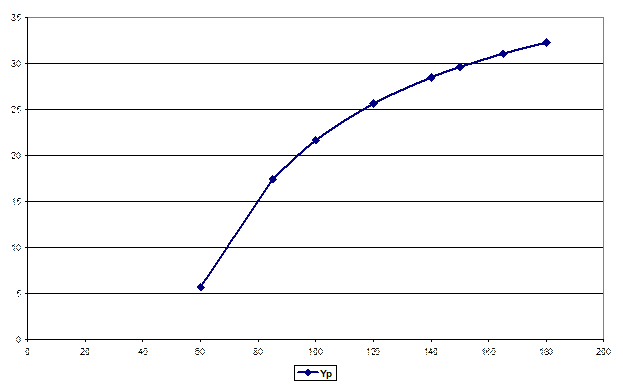
Рис. 18. Кривая Энгеля

Кривая Энгеля полезна также при определении степени влияния на спрос дохода и изменений в относительных ценах.

Пример

Пусть зависимая переменная y – средняя заработная плата продавцов (в тыс. руб.) в семи различных торговых точках, а фактор x – чистая среднемесячная прибыль (в тыс. руб.) в них (исходные данные приведены в таблице 1).

Таблица 1

n	y	x

Требуется:

1. Построить степенную, показательную и гиперболическую модели нелинейной регрессии. Результаты моделирования отобразить на графике.

2. Сравнить качественные характеристики моделей, рассчитав коэффициенты детерминации и средние относительные ошибки аппроксимации.

Решение:

Степенная модель

.

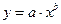Линеаризация:

,

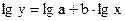обозначим lg y=Y, lg x= X, и получим вспомогательную линейную модель вида

Y=A+bX.

Для ее построения воспользуемся таблицей 2 (столбцы X=lg x и Y=lg y) и результатами регрессионного анализа.

Таблица 2

n	y	x	lg y=Y	lg x=X	yp	ei	ei^2	eiотн	y-ycp	(y-ycp)^2
			0.301	1.699	2.464	-0.464	0.215	23.200	-14.286	204.082
			0.602	1.778	4.097	-0.097	0.009	2.427	-12.286	150.939
			1.041	1.929	10.823	0.177	0.031	1.606	-5.286	27.939
			1.230	1.929	10.823	6.177	38.151	36.333	0.714	0.510
			1.255	2.000	17.030	0.970	0.941	5.389	1.714	2.939
			1.447	2.079	28.317	-0.317	0.101	1.133	11.714	137.224
			1.531	2.146	43.527	-9.527	90.773	28.022	17.714	313.796
Сумма							130.222	98.110		837.429
Среднее	16.286	91.429						14.016

Вспомогательная линейная модель примет вид

Y=-4.346+2.789*X.

Обратный переход к степенной функции:

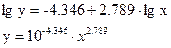
Степенная модель парной регрессии примет вид:

.

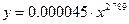С помощью этой модели рассчитываем все последующие столбцы таблицы 1, начиная с 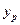и далее.

Качественные характеристики модели:

–

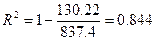84.4 % случайной вариации переменной средняя заработная плата (y) учтено в построенной модели и обусловлено случайными колебаниями фактора чистая прибыль (х);

–

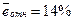фактические значения средней зарплаты отличаются от рассчитанных на основе степенной модели в среднем на 14 %.

График:

x	y	yp
		2.464
		4.097
		10.823
		10.823
		17.030
		28.317
		43.527

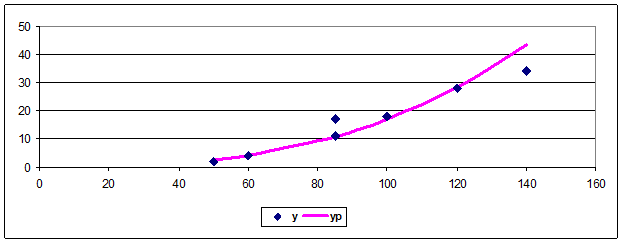
Показательная модель

.

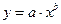Линеаризация:

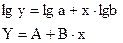
Таблица 3

n	y	x	lg y=Y	yp	ei	ei^2	eiотн
			0.301	3.119	-1.119	1.252	55.954
			0.602	4.245	-0.245	0.060	6.125
			1.041	9.173	1.827	3.339	16.611
			1.230	9.173	7.827	61.265	46.042
			1.255	14.564	3.436	11.807	19.089
			1.447	26.976	1.024	1.048	3.657
			1.531	49.967	-15.967	254.929	46.960
Сумма						333.700	194.439
Среднее	16.286	91.429					27.777

Y=-0.161+0.0133*x – вспомогательная линейная модель.

Обратный переход:

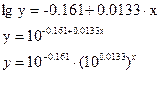
Окончательно показательная модель примет вид:

.

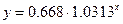Качественные характеристики модели:

–

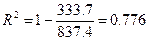77,6 % случайной вариации переменной средняя заработная плата (y) учтено в построенной модели и обусловлено случайными колебаниями фактора чистая прибыль (х);

–

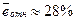фактические значения средней зарплаты отличаются от рассчитанных на основе модели в среднем на 28 %, модель неточная.

График:

x	y	yp
		3.119
		4.245
		9.173
		9.173
		14.564
		26.976
		49.967

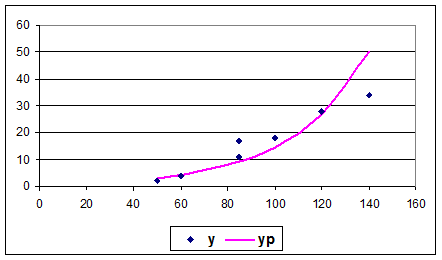
Гиперболическая модель

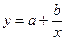
Линеаризация:

используем простую замену ,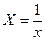

.

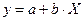Таблица 4

n	y	x	1/x=X	yp	ei	ei^2	eiотн
			0.02	-2.298	4.2983	18.475	214.9137
			0.0167	5.6834	-1.683	2.8338	42.08507
			0.0118	17.421	-6.421	41.231	58.37421
			0.0118	17.421	-0.421	0.1774	2.477429
			0.01	21.647	-3.647	13.299	20.25976
			0.0083	25.638	2.3624	5.581	8.437161
			0.0071	28.488	5.5118	30.38	16.21119
Сумма						111.98	362.7585
Среднее	16.286	91.429					51.82265

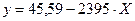– вспомогательная линейная модель;

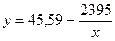– гиперболическая модель.

Качественные характеристики модели:

–

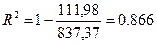86,6 % случайной вариации переменной средняя заработная плата (y) учтено в построенной модели и обусловлено случайными колебаниями фактора средняя чистая прибыль (х);

–

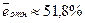фактические значения средней зарплаты отличаются от рассчитанных на основе модели в среднем на 51,8 %, модель неточная.

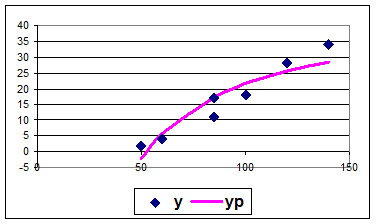
График:

x	y	yp
		-2.298
		5.6834
		17.421
		17.421
		21.647
		25.638
		28.488

Сравнение моделей

Таблица 5

Модель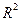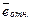
Степенная	0.844	14.02
Показательная	0.776	27.78
Гипербoлическая	0.866	51.8

Общие сведения о регрессионном анализе

Регрессионный анализпредназначен для исследования количественных взаимосвязей переменных и представления их в виде регрессионной модели.

Виды регрессий:

1) по числу переменных:

- парная,

- множественная,

- частная;

2) по виду связи переменных:

- линейная,

- нелинейная;

3) по направлению связей:

- положительная,

- отрицательная.

Задачи регрессионного анализа:

1. Установление формы связи, построение модели.

2. Оценка качества моделей.

3. Распределение факторов по степени влияния на показатель.

4. Построение прогноза.

Общий вид регрессионной модели: