Лекция 1. Множественный регрессионный анализ

Лекция 1. Множественный регрессионный анализ

Классическая нормальная линейная модель множественной регрессии

Экономические явления, как правило, определяются большим числом одновременно и совокупно действующих факторов. В связи с этим часто возникает задача исследования зависимости одной зависимой переменной у от нескольких объясняющих переменных х₁, … , х_k. Эта задача решается с помощью множественного регрессионного анализа.

Имеется n наблюдений. Обозначим i-е наблюдение зависимой переменной y_i, а объясняющих переменных x_i1, x_i2,… x_ik. Тогда модель множественной линейной регрессии можно представить в виде:

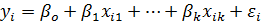(1)

где i = 1, 2, … , n число наблюдений.

ε_i – регрессионные ошибки случайного характера.

Основные гипотезы

Гипотезы, лежащие в основе модели множественной регрессии, являются естественным обобщением модели парной регрессии:

1. 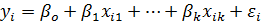, i = 1, …, n – спецификация модели.

2. x_i1, x_i2,… x_ik – детерминированные (неслучайные) величины. Векторы x_s =(x_1s, …, x_ns)^Т s = 1, …, k линейно независимы в Rⁿ.

3. a. М(ε_t) = 0, т.е. математическое ожидание ошибки равно нулю. М( 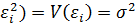– не зависит от номера наблюдения i. Означает неизменность дисперсий регрессионной ошибки. (Это свойство наз. гомоскедастичностьюрегрессионной ошибки).

3. b. М(ε_i,ε_j)=0 при i≠j – статистическая независимость (некоррелированность друг с другом) ошибок для разных наблюдений. Некоррелированность ошибок означает, что результат наблюдений одного объекта не может повлиять на результат наблюдений другого.

3. c. Ошибки ε_i, i=1,…,n имеют совместное нормальное распределение ε_i~N(0,σ²).

В этом случае модель называется классическойнормальной линейной регрессионной.

Гипотезы, лежащие в основе множественной регрессии удобно записать в матричной форме, которая будет использоваться в дальнейшем.

Пусть:

Y обозначает 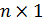матрицу (вектор-столбец) (y₁,…, y_n)^Т (Т вверху означает транспонирование),

В = (β₀, β₁, …, β_к)^Т – 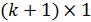вектор-столбец коэффициентов (неизвестных значений параметров модели),

Е = (ε₁, ε₂, …, ε_n)^Т – 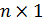вектор-столбец ошибок,

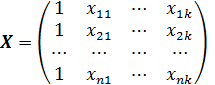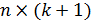- матрицу объясняющих переменных, которая соответствует набору векторов-столбцов объясняющих переменных, а также вектору-столбцу из единиц, отвечающему за константу в уравнении модели. Матрица должна быть матрицей полного ранга.

- единичная матрица размерности ;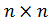

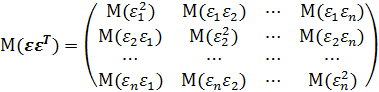- ковариационная матрица размерности 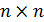вектора ошибки.

Условия 1-3 в матричной записи выглядят следующим образом:

1. Y=XВ+Е – спецификация модели;

2. X – детерминированная матрица, имеет максимальный ранг k+1;

3. a,b. М(ε)=0; V(ε)=М(εε^T)=σ²I_n;

дополнительное условие:

3. с. Е~N(0,σ²I_n), т.е. Е – нормально распределенный случайный вектор со средним и матрицей ковариаций σ²I_n(нормальная линейная регрессионная модель).

Оценкой этой модели по выборке является уравнение:

Y=X 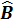+Е,

Где 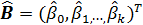– вектор-столбец оценок неизвестных параметров модели;

E = (e₁, e₂, …, e_n)^Т – вектор –столбец регрессионных остатков.

Теорема Гаусса-Маркова.

Предположим, что:

1. Y=XB+E;

2. X – детерминированная матрица, имеет максимальный ранг k+1

3. М(ε)=0; V(ε)=М(εε^T)=σ²I_n.

Тогда оценка метода наименьших квадратов 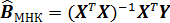является наиболее эффективной (в смысле наименьшей дисперсии) оценкой в классе линейных (по y) несмещенных оценок.

1.3 Анализ вариации зависимой переменной в регрессии. Коэффициенты R2 и скорректированный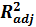

Для регрессионной модели известны следующие величины дисперсий:

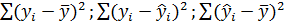где 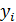– значение зависимой переменной по исходным данным, 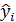- значение зависимой переменной, вычисленное по регрессионной модели, 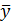- среднее значение зависимой переменной, определенное по исходным статистическим данным. Для указанных дисперсий справедливо равенство

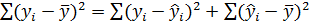
Как и в случае регрессионной модели с одной независимой переменной, вариацию 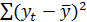можно разбить на две части: объясненную регрессионным уравнением и необъясненную ( т.е. связанную с ошибками ε).

Поэтому верно равенство

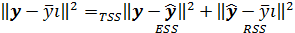(7)

Записывая (7) в отклонениях 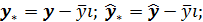получим теорему Пифагора:

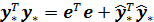(8)

Определим коэффициент детерминации 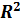как

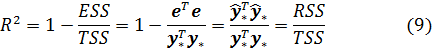
Отметим, что коэффициент R² корректно определен только в том случае, если константа, т.е. вектор 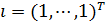, принадлежит линейной оболочке векторов 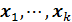. В этом случае R² принимает значения из интервала [0,1].

Коэффициент R² показывает качество подгонки регрессионной модели к наблюдаемым значениям y_t.

Если R²=0, то регрессия 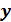на 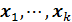не улучшает качество предсказания y_t по сравнению с тривиальным предсказанием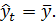

Другой крайний случай R²=1 означает точную подгонку: все e_t=0, т.е. все точки наблюдений удовлетворяют уравнению регрессии.

Пример другого обозначения: Для модели регрессии вида 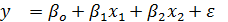, где 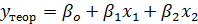, рассчитаны дисперсии 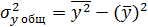, , 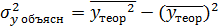, 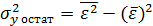тогда величина коэффициента детерминации рассчитывается по формуле 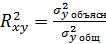или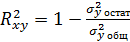

В какой степени допустимо использовать критерий R² для выбора между несколькими регрессионными уравнениями? Следующие два замечания побуждают не полагаться только на значение R².

1. R², вообще говоря, возрастает при добавлении еще одного регрессора.

2. R² изменяется даже при простейшем преобразовании зависимой переменной, поэтому сравнивать по значению R² можно только регрессии с одинаковыми зависимыми переменными.

Если взять число регрессоров равным числу наблюдений, всегда можно добиться того, что R²=1, но это вовсе не будет означать наличие содержательной (имеющей экономический смысл) зависимости у от регрессоров.

Попыткой устранить эффект, связанный с ростом R² при возрастании числа регрессоров, является коррекция R² на число регрессоров.

Скорректированным (adjusted) R² называется

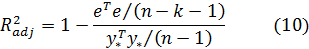
Заметим, что нет никакого существенного оправдания именно такого способа коррекции.

Свойства скорректированного R²:

1.

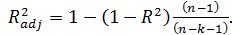
2.

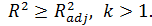
3. 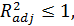но может принимать значения < 0.

В определенной степени использование скорректированного коэффициента детерминации 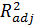, более корректно для сравнения регрессий при изменении количества регрессоров.

Скорректированный коэффициент детерминации применяется для оценки реальной тесноты связи между результатом и факторами и сравнения моделей с разным числом параметров.

В классической множественной линейной регрессии абсолютным показателем силы связи результата с фактором 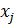является коэффициент 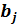при соответствующем факторе.

Коэффициенты 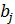линейной модели множественной регрессии называют коэффициентами условно-чистой регрессии. Они показывают на сколько единиц в среднем изменится результат при изменении фактора 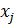на 1 при фиксированном уровне других факторов, включенных в модель.

В классической множественной линейной регрессии относительным показателем силы связи результата с фактором 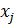является коэффициент эластичности

Коэффициенты эластичности показывают на сколько процентов в среднем изменится результат при изменении фактора 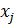на 1% и значениях других факторов, фиксированных на средних уровнях.

В множественной регрессии показателями тесноты связи являются: коэффициент множественной корреляции и коэффициент множественной детерминации.

Проверка гипотез.

Предпосылки МНК

Условия, необходимые для получения несмещенных, состоятельных и эффективных оценок представляют собой предпосылки МНК, соблюдение которых желательно для получения достоверных результатов регрессии.

К предпосылкам МНК относятся следующие условия:

- случайный характер остатков

- нулевая средняя величина остатков, не зависящая от х_i

- гомоскедастичность (дисперсия каждого отклонения 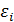одинакова для всех значений х )

- отсутствие автокорреляции остатков. Значения остатков 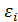распределены независимо друг от друга

- остатки подчиняются нормальному распределению

Гетероскедастичность остатков означает, что дисперсия каждого отклонения 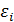неодинакова для разных значений

К тестам, позволяющим выявить наличие гетероскедастичности остатков относят тесты Гольдфельда-Квандта, ранговой корреляции Спирмэна, Уайта, Парка, Глейзера.

Шаги параметрического теста Гольдфельда-Квандта:

Шаг 1 Упорядочение n наблюдений по мере возрастания переменной х

Шаг 2 Исключение из рассмотрения С центральных наблюдений; при этом 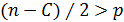, где p – число оцениваемых параметров.

Шаг 3 Разделение совокупности из (n-C) наблюдений на две группы (соответственно с малыми и большими значениями фактора х) и определение по каждой из групп уравнений регрессии.

Шаг 4 Определение остаточной суммы квадратов для первой ( 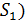и второй ( 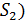групп и нахождение их отношения: 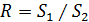, где .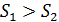

К методам определения автокорреляции остатков относятся:

- визуальный (построение графика зависимости остатков от времени)

- аналитический (использование критерия Дарбина-Уотсона)

Если в остатках существует полная положительная автокорреляция то значение критерия Дарбина-Уотсона 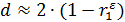равно 0

Если в остатках существует полная отрицательная автокорреляция то значение критерия Дарбина-Уотсона 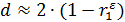равно 4

Если автокорреляция остатков отсутствует то значение критерия Дарбина-Уотсона 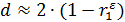равно 2

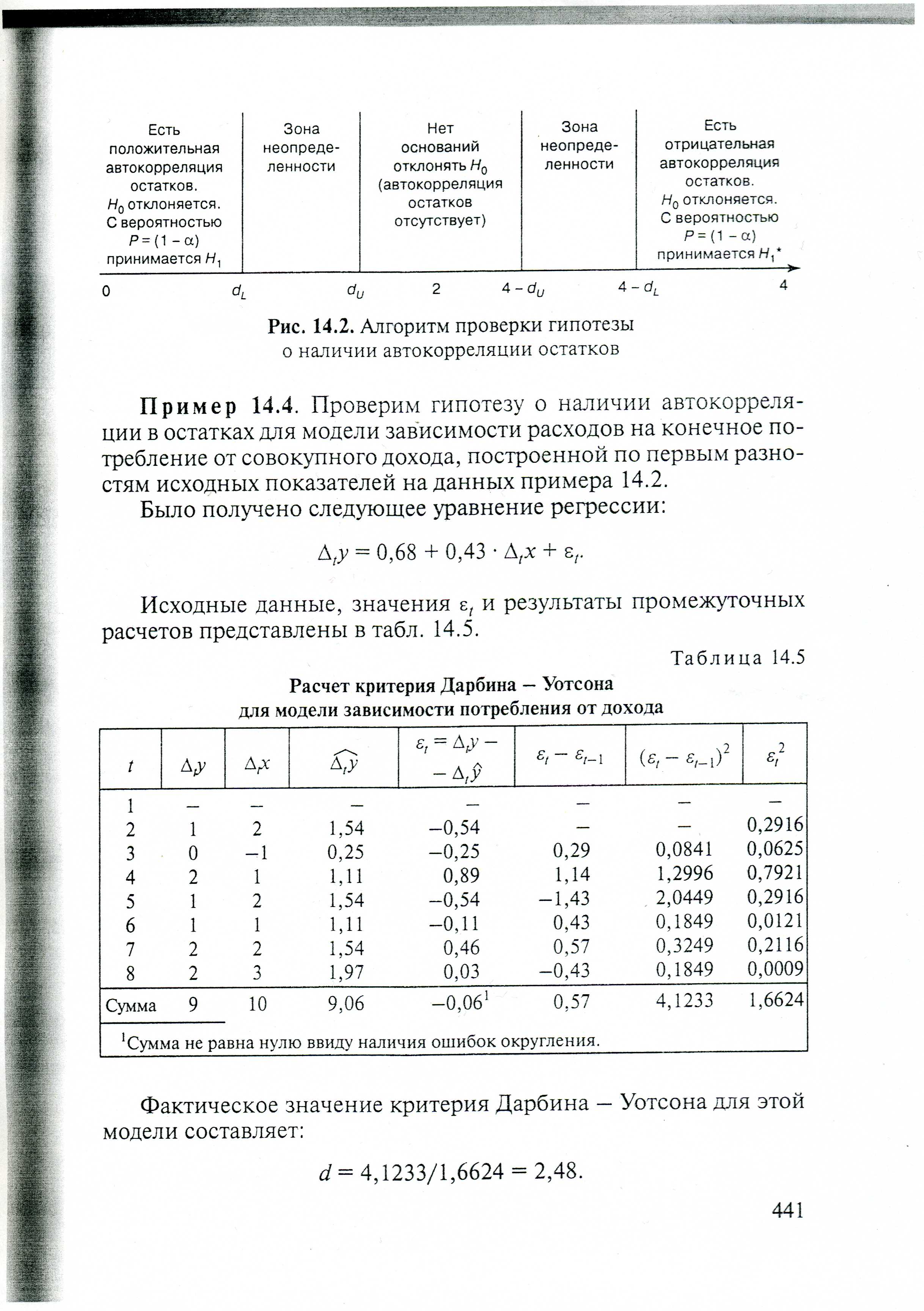
Шаги алгоритма выявления автокорреляции остатков на основе критерия Дарбина-Уотсона:

Шаг 1 Выдвигается гипотеза Н₀ об отсутствии автокорреляции остатков. Альтернативные гипотезы Н₁ и Н₁^* состоят соответственно в наличии положительной или отрицательной автокорреляции остатков.

Шаг2 По специальным таблицам определяются критические значения критерия Дарбина-Уотсона d_L и d_U для заданного числа наблюдений n, числа независимых переменных модели k и уровня значимости α. По этим значениям числовой промежуток [0,4] разбивают на пять отрезков.

Шаг3 Принимают или отклоняют каждую из гипотез с вероятностью (1- α) по соответствующей шкале.

Если фактическое значение критерия Дарбина-Уотсона попадает в зону неопределенности, то предполагают существование автокорреляции остатков и отклоняют гипотезу Н₀

Если фактическое значение критерия Дарбина-Уотсона 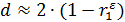попадает в интервал от 0 до d_L то можно сказать, что есть положительная автокорреляция остатков

Если фактическое значение критерия Дарбина-Уотсона 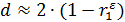попадает в интервал от (4- d_L ) до 4. В этом случае можно сказать, что есть отрицательная автокорреляция остатков

Если фактическое значение критерия Дарбина-Уотсона 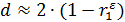попадает в интервал от d_U до (4- d_U). В этом случае можно сказать, что автокорреляция остатков отсутствует

В случае нарушений предпосылок метода наименьших квадратов применяют обобщенный метод наименьших квадратов, который используется для оценки параметров линейных регрессионных моделей с автокоррелированными и/или гетероскедастичными остатками

При использовании обобщенного метода наименьших квадратов расчеты параметров уравнения регрессии с учетом значений ковариационной матрицы остатков 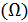могут быть проведены по формуле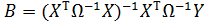

Фиктивные переменные

Фиктивная переменная может принимать значения 0 или 1.

С помощью фиктивной переменной можно в уравнении регрессии количественным образом оценить влияние качественных признаков.

При построении регрессионной модели может возникнуть ситуация, когда необходимо включить в уравнение помимо количественных переменных переменные, отражающие некоторые атрибутивные признаки (пол, образование, регион и т.п.). Такого рода качественные переменные называются «фиктивными» (dummy) переменными. Они отражают неоднородность исследуемой статистической совокупности и используются для более качественного моделирования зависимостей в таких неоднородных объектах наблюдения. При моделировании отдельных зависимостей по неоднородным данным можно также воспользоваться способом разделения всей совокупности неоднородных данных на несколько отдельных совокупностей, количество которых равно количеству состояний dummy-переменной.

Лекция 1. Множественный регрессионный анализ