Практическое занятие №5 (1ч)

Решение дифференциальных уравнений первого порядка

1. Определить порядок дифференциального уравнения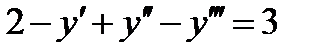

2. Определить является ли функция 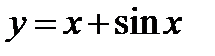решением дифференциального уравнения ?

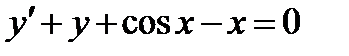3. Найти общее решение дифференциального уравнения .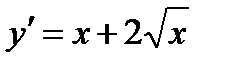

4. Найти общее и частное решение дифференциального уравнения с разделяющимися переменными 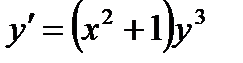при .

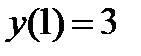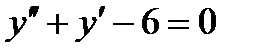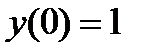5. Найти общее и частное решение однородного дифференциального уравнения второго порядка с постоянными коэффициентами при и .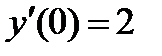

Тема 8. Комбинаторика, теория графов, теория вероятностей.

Содержание программы

8.1. Элементы комбинаторики: перестановки, размещения, сочетания.

8.2. Понятие графа, простейшие свойства. Способы задания графов. Использование графов для решения задач.

8.3. Основные понятия теории вероятностей. Действия над событиями.

8.4. Классическая и геометрическая вероятность, их своиства.

8.5. Теоремы сложения и умножения вероятностей. Зависимые и независимые события. Условная вероятность.

Содержание темы

Графы, их способы задания

Граф – множество точек (вершин графа), часть из которых соединена линиями (ребрами или дугами графа).

Ребро, соединяющее вершину с ней же, называется петлей.

Если вершины соединяются направленными линиями (дугами графа), то граф называют ориентированным (орграфом).

Вершины графа, связанные ребром, называются смежными. В таком случае говорят, что их общее ребро инцидентно обеим вершинам.

Если граф ориентированный, то одна из вершин дуги является начальной, а вторая – конечной.

Степенью вершины называется количество ребер, ей инцидентных. В орграфе число дуг, входящих в вершину и выходящих из нее, называется соответственно полустепенью входа и полустепенью выхода вершины.

Простейшие свойства степеней вершин графа:

1. Сумма степеней вершин графа равна удвоенному числу его ребер.

2. Число вершин нечетной степени четно.

Вершина, не инцидентная никакому ребру, называется изолированной.

Граф, состоящий только из изолированных вершин, называется пустым или нуль-графом.

Граф называется полным, если любые две его вершины являются смежными.

Подграф заданного графа – это граф, множества вершин и ребер которого являются подмножествами соответственно множеств вершин и ребер исходного графа.

Маршрут (путь) – чередующаяся последовательность вершин и ребер, в которой каждые два соседних элемента инцидентны.

Количество ребер при этом называется длиной маршрута.

Цепь – маршрут, в котором все ребра различны.

Простая цепь – цепь, в которой все вершины различны.

Цикл (простой цикл) – замкнутая (простая) цепь.

Граф называется связным, если для любых двух его вершин найдется соединяющий их маршрут. Если хотя бы для одной пары вершин это свойство не выполняется, то граф называется несвязным.

Цикл, проходящий через все ребра графа ровно один раз, называется эйлеровым, а граф, его содержащий, - эйлеровым графом. Связный граф является эйлеровым тогда и только тогда, когда все его вершины четной степени.

Цикл, проходящий через все вершины графа ровно один раз, называется гамильтоновым, а граф, его содержащий, - гамильтоновым графом.

Дерево – связный неориентированный граф без циклов.

Корневое дерево – дерево, в котором выделена одна из вершин (корень).

Способы задания графа:

1. Графический: вершины графа изображаются точками, а ребра и дуги – линиями, их соединяющими (в дугах указывается направление с помощью стрелки).

2. Аналитический: представляется описание множеств 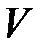и 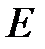, так как граф 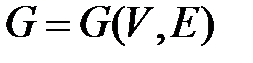может быть определен как совокупность двух множеств: 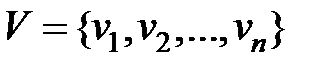, элементы которого называются вершинами, и 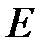- произвольное множество пар 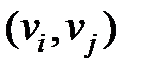, элементы которого называются дугами.

3. Матричный: используются матрицы графов.

Матрица смежности неориентированного графа 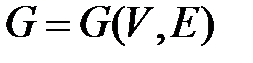- квадратная матрица 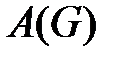порядка 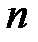, где 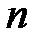- количество вершин. Ее элементы 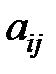равны числу ребер, соединяющих вершины 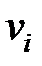и .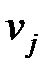

Пример 8.1.В поселке 6 стационарных телефонов. Можно ли каждый из них соединить кабелем ровно с тремя другими? Изменится ли ответ, если добавить еще один телефон?

Решение: Построим граф, вершины которого будут соответствовать телефонам, а ребра – проводам, их соединяющим. По условию задачи каждый телефон должен быть соединен ровно с тремя другими. Соединим каждую вершину графа ровно с тремя другими, например, так, как показано на рис. 1.

Если телефонов станет 7, то, согласно второму свойству степеней вершин графа, требуемую схему реализовать невозможно. Действительно, степень каждой вершины по условию должна быть равна трем (каждый телефон соединен ровно с тремя другими, т.е. каждая вершина графа инцидентна трем ребрам). Получается, что в графе количество вершин нечетной степени нечетно, а этого не может быть. Значит, при добавлении одного аппарата соединение не может быть реализовано.

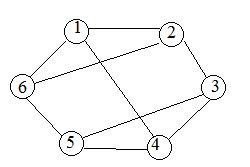Рис. 1

Элементы комбинаторики

Пусть имеется множество, содержащее n элементов. Каждое его упорядоченное подмножество, состоящее из k элементов, называется размещением из n элементов по k элементов.

Число размещений из n элементов по k элементов равно произведению k последовательных натуральных чисел от n до n-k+1 включительно, т.е.

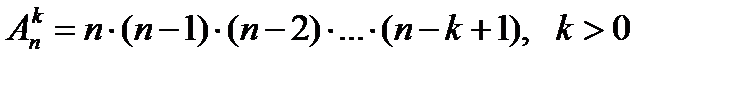или

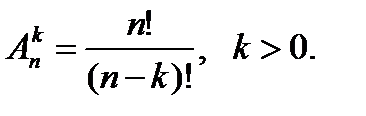
Размещения из n элементов по n элементов называются перестановками из n элементов.

Число перестановок из n элементов равно n!.

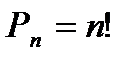
Пусть имеется множество, содержащее n элементов. Каждое его подмножество, состоящее из k элементов, называется сочетанием из n элементов по k элементов.

Число сочетаний из n элементов равно произведению всех натуральных чисел от n до n –k+1 включительно, деленному на k!

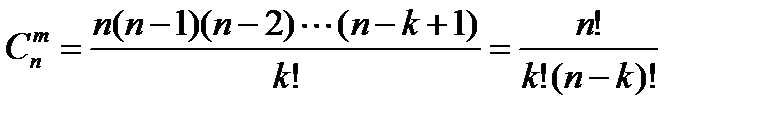
Пример 8.2. Группа учащихся изучает 10 учебных дисциплин. Сколькими способами можно составить расписание занятий на понедельник, если в этот день недели должно быть четыре различных урока?

Решение

Число способов, которыми можно распределить четыре дисциплины из 10, равно числу упорядоченных выборок объёма 4 из множества, содержащего 10 элементов, т.е. числу размещений из 10 элементов по 4. По формуле, полагая в ней n=10, k=4 , получаем

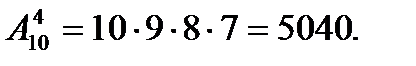
Ответ: 5040.

Пример 8.3. Сколько матчей будет сыграно в футбольном чемпионате с участием 16 команд, если каждые две команды встречаются между собой один раз?

Решение

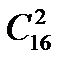Число матчей равно числу неупорядоченных выборок объема 2 из множества, содержащего 16 элементов, т. е. равно . По формуле числа сочетаний находим

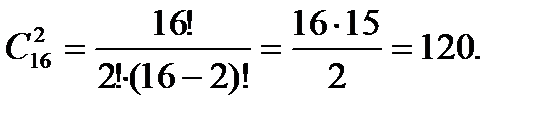
Ответ: 120.

Вероятность и ее свойства

Вероятностью Р(А) события А, связанного с опытом с равновероятными исходами, называется отношение числа исходов, благоприятствующих событию А, к числу всех исходов.

Таким образом, если n - число всех исходов, k - число исходов, благоприятствующих событию А, то

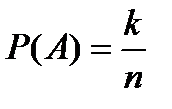
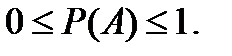
Пример 8.4. В урне находятся 4 черных и 6 белых шаров. Найти вероятность того, что вынутый наудачу шар будет белым.

Решение

Здесь число благоприятных исходов (количество белых шаров k=6), количество всех исходов (количество всех шаров n=10), тогда

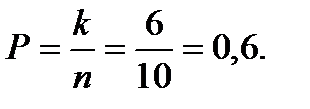
Ответ: 0,6.

Пример 8.5. Среди 100 электроламп 5 испорченных. Какова вероятность того, что выбранные наудачу 3 лампы окажутся исправными?

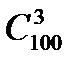Решение

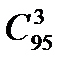Из 100 электроламп 3 лампы можно выбрать способами. Три исправных лампы из общего числа 95 исправных ламп можно выбрать

способами. Следовательно, искомая вероятность равна

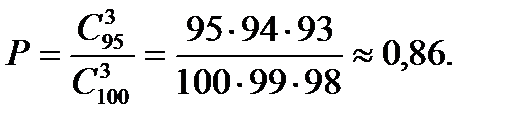
Ответ: 0,86.

Контрольные вопросы

1. Что называется графом?

2. Как определяется степень вершины графа?

3. Назовите свойства степеней вершин.

4. Дайте определение маршруту.

5. Что называется циклом в графе?

6. Какой граф называется эйлеровым?

7. Дайте определение дереву.

8. Какими способами можно задать граф?

9. Что называется размещением и как вычисляется число размещений из n элементов по m элементов?

10. Что называется сочетанием и как вычисляется число сочетаний из n элементов по m элементов?

11. Что называется перестановкой и как вычисляется число перестановок из n элементов?

12. Что называется вероятностью события?

13. Назовите свойства вероятности.

14. Сформулируйте основные теоремы теории вероятностей.