Определение и алгебраическая форма комплексных чисел

ВВЕДЕНИЕ

Методическое пособие учебной дисциплины «Прикладная математика» разработана на основе Федеральных государственных образовательных стандартов (далее ФГОС) по специальностям среднего профессионального образования (далее СПО):

190701 «Организация перевозок и управление на транспорте (по видам)»

220415 «Автоматика и телемеханика на транспорте (на железнодорожном транспорте)».

Пособие включает материалы по следующим разделам прикладной математики:

Комплексные числа;

Дифференциальное исчисление;

Интегральное исчисление.

Перечень рекомендуемых учебных изданий, интернет-ресурсов, дополнительной литературы

Основные источники:

1. Дадаян А.А. Математика: учебник – 2-е издание, учебник для студ. учреждений СПО. М.: Форум-инфра-М., 2007. -544 с.-(профессиональное образование) .

2. Дадаян А.А. Сборник задач по математике, учеб. пособие для студ. учреждений СПО – М.: Форум-инфра-М., 2005.- 352 С.

Дополнительные источники:

3. Щипачев В.С. Высшая математика. учеб. пособие для студ. высш. учеб. завед.. / В. С. Щипачев. - 8-е изд., стер. – М. : Высш. шк., 2006. – 480 с.

4. Математика. Часть I. Алгебра и элементарные функции. Геометрия. Контрольные задания для учащихся заочных средних учебных заведений. М. «Высшая школа», 1969 г.

5. Математика. Контрольные задания для специальностей промышленности, транспорта, связи, строительства, сельского хозяйства и отдельных экономических специальностей заочных средних специальных учреждений. М. «Высшая школа», 1981 г.

Интернет-ресурсы:

6. http://www.twirpx.com/files/mathematics - конспекты лекций, методические пособия по дисциплине «Математика»

7. http://allmatematika.ru/ - бесплатный каталог учебной литературы по математике

8. http://www.pm298.ru/opredelen9.php

КОМПЛЕКСНЫЕ ЧИСЛА

Определение и алгебраическая форма комплексных чисел

Комплексными числаминазываются выражения вида 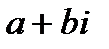, (где а и b действительные числа, а 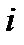- символ, удовлетво­ряющий условию 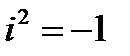), при условии, что для этих выражений равенство, сложение и умножение определя­ются следующим образом:

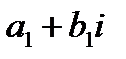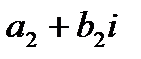а) два комплексных числа и считаются равными тогда и только тогда, когда 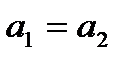и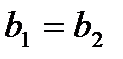

б) суммой двух комплексных чисел 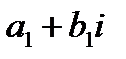и 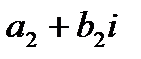назы­вается комплексное число 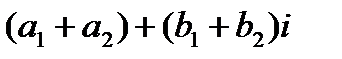(1.1),

в) произведением двух комплексных чисел 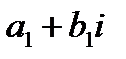и 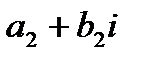на­зывается комплексное число 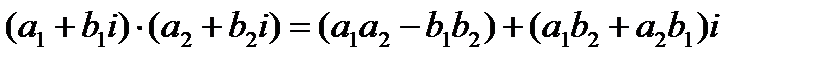(1.2).

Пример. 1.1. Вычислить сумму и произведение двух комплексных чисел: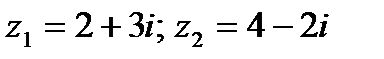

Решение.

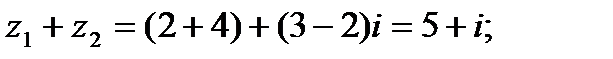
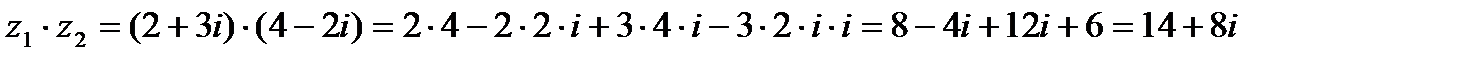
Из приведенных примеров видно, что формулы (1.1) и (1.2.) помнить необязательно. Сложение и умножение комплексных чисел можно выполнять по правилам сложения и умножения двучленов.

Разность двух комплексных чисел – операция обратная сложению и может быть выполнена по формуле: 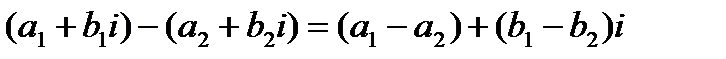(1.3).

Пример 1.2. Вычислить разность двух комплексных чисел: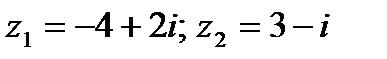

Решение

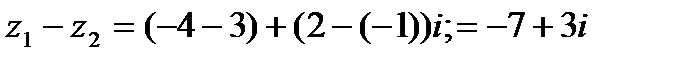
Из приведенного примера видно, что формулу (1.3) помнить необязательно. Вычитание комплексных чисел можно выполнять по правилам вычитания двучленов

Число 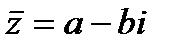называется комплексно-сопряженным с комп­лексным числом 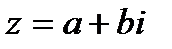. Понятие комплексной сопряженности взаимно.

Сумма и произведение комплексно-сопряженных чисел со­ответственно равны 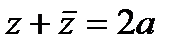и .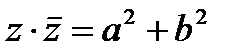

Частноеот деления одного комплексного числа на второе – операция обратная умножению и может быть выполнена по формуле:

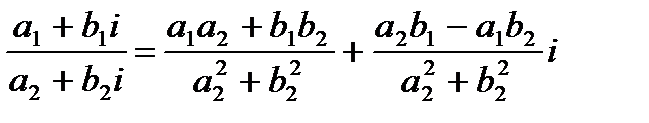(1.4)

Эту формулу можно не запоминать, а руководствоваться следующим правилом: для того, чтобы разделить одно комплексное число на другое, надо записать их в виде дроби, в числителе которой – делимое, а в знаменателе – делитель, а затем числитель и знаменатель умножить на число, сопряженное со знаменателем.

Покажем справедливость этого правила:

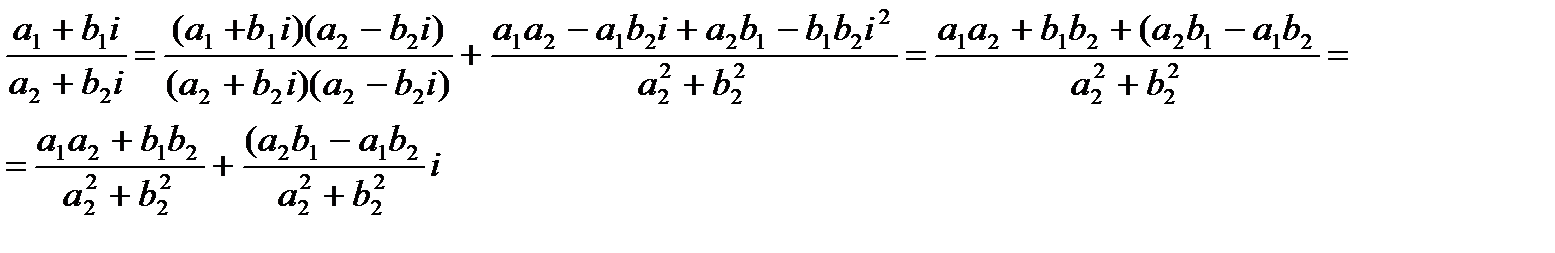
Как можно увидеть, получившееся в результате использования приведенного выше правила деления комплексных чисел совпадает с правой частью формулы (1.4), что свидетельствует о справедливости этого правила.

Пример 1.3.

Вычислить частное от деления комплексного числа 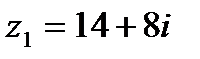на комплексное число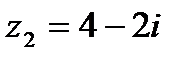

Решение

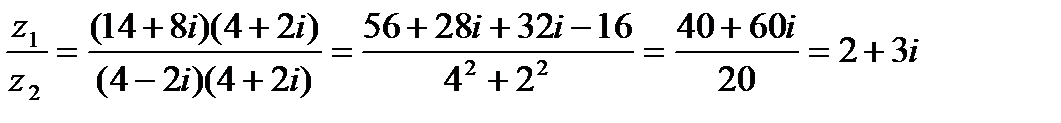
В этом примере использованы по сути те же данные, что и во втором из примеров 1.1. В данном случае делимое – результат перемножения комплексных чисел примера 1.1. Делитель – второй из сомножителей упомянутого примера. Частное от деления в текущем примере совпало с первым сомножителем примера 1.1., что подтверждает правильность выполненной нами операции деления.

Комплексное число равно нулю тогда и только тогда, ког­да .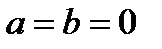

Для комплексных чисел, так же, как и для векторов, нет по­нятия больше и меньше.

Покажем, как в множестве комплексных чисел решаются квадратные уравнения, дискриминанты которых меньше нуля.

Пусть, например, нужно решить уравнение 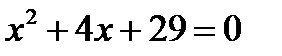. Легко подсчитать, что

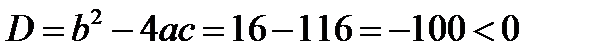
Сле­довательно,

.

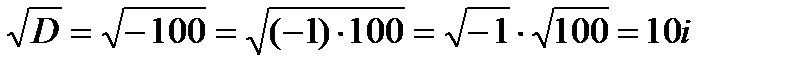Поэтому

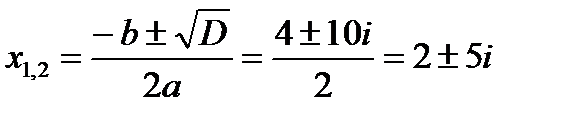
То есть, квадратное уравнение с действительными ко­эффициентами и отрицательным дискриминантом имеет два комплексно-сопряженных корня.

Операция возведения в степень комплексного числа рассмат­ривается как частный случай произведения одного и того же со­множителя.

Степени мнимой единицы даются формулой

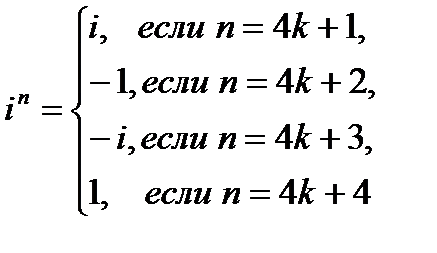
Например,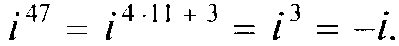

Пример 1.4. Найти действительные числа х и yиз уравнения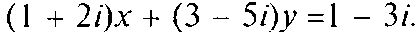

Решение.Используем условия равенства двух комплексных чисел 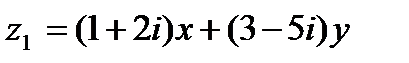и .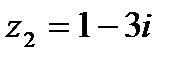

Пользуясь определени­ем суммы, получаем 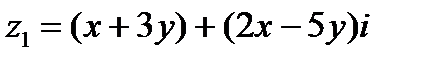Сравнивая действите­льные и мнимые части чисел z₁ и z₂, получим систему двух урав­нений относительно х и у 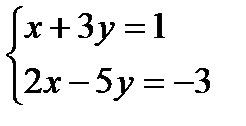, решением которой будет .

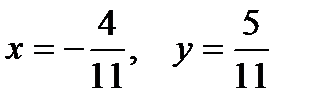Решение.

а) Центральной симметрией относительно точки A называют преобразование пространства, переводящее точку X в такую точку X′, что A — середина отрезка XX′ (см. рис.).

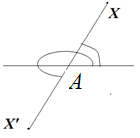Поэтому, в каждой из приведенных точек величина радиус-вектора r останется прежней, а угол 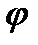изменится на величину 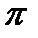. Таким образом, координаты точек, симметричных с указанными точками относительно начала координат, будут: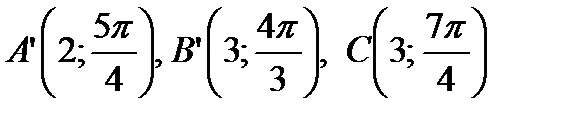

б) Для того, чтобы построить на плоскости точку 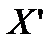, симметричную точке 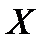относительно прямой l, необходимо от этой точки провести перпендикуляр к прямой и отложить на продолжении этого перпендикуляра точку 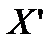на расстоянии, равном расстоянию от точки до прямой (см. рис.).

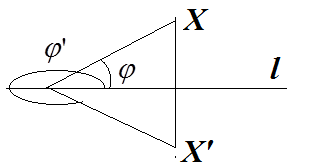Из приеденного рисунка видно, что в точке , симметричной точке , радиус-вектор равен радиус - вектору точки 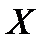, а угол .

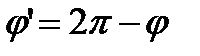Таким образом, координаты точек, симметричных с указанными точками относительно оси 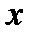, будут: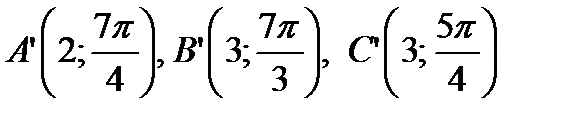

Пример 1.7. Определите полярные координаты точек

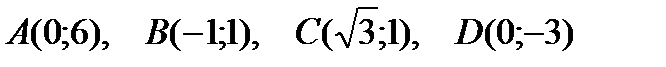
Решение:

Точка A: ;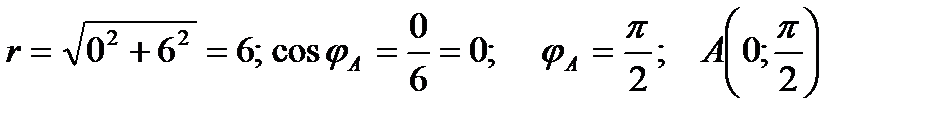

Точка B: ;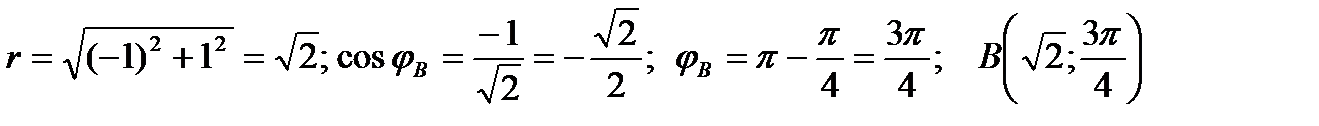

Точка C: ;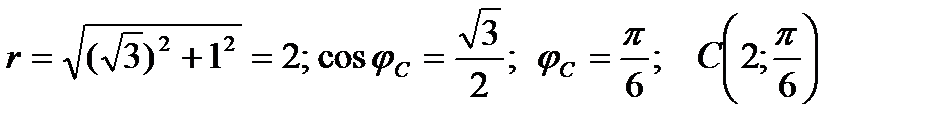

Точка D: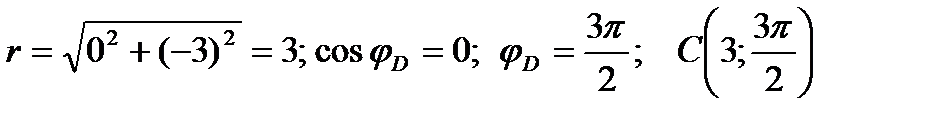

Аналогично тому, как на числовой прямой откладываются точки с декартовыми координатами, на плоскости можно откла­дывать точки, соответствующие комплексным числам.

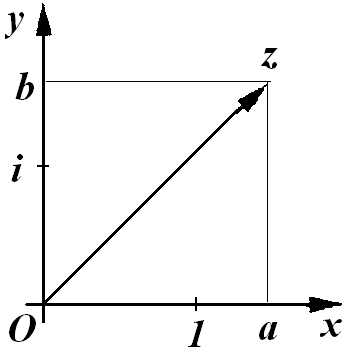Пусть дано множество комплек­сных чисел C и 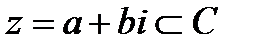- произвольное комплексное число.

За единицу на оси Ox примем дей­ствительное число 1, а на оси Оу - мнимую единицу 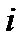. Такая плоскость называется комплексной плоскостью.

Пример 1.7. Данные числа изобразите на комплексной плоскости

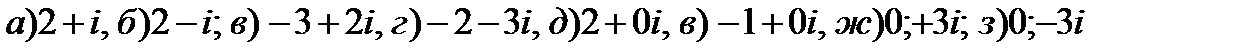Решение

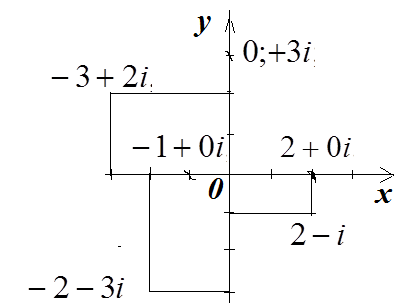
Решение.

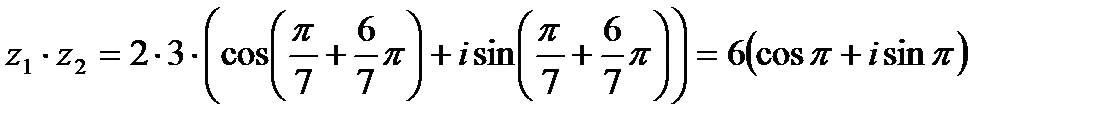
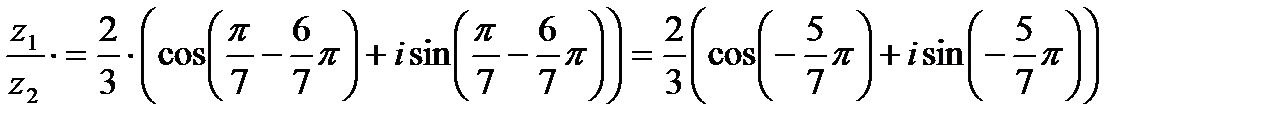
Пример 1.10. Дано комплексное число в алгебраической форме: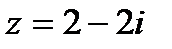

а) перевестиего в тригонометрическую форму;

б) возвести в четвертую степень;

в) извлечь корень третьей степени.

Решение.

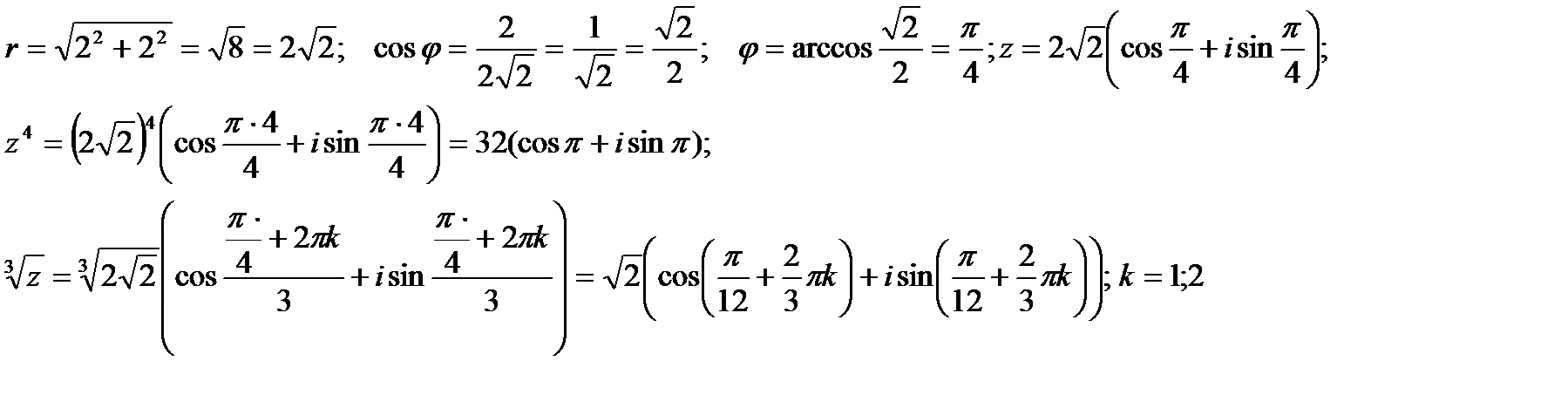
Решение

а) ;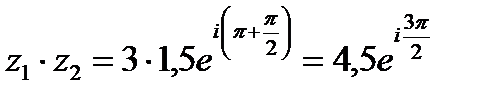

б)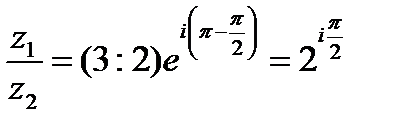

ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ

Л Построение графика

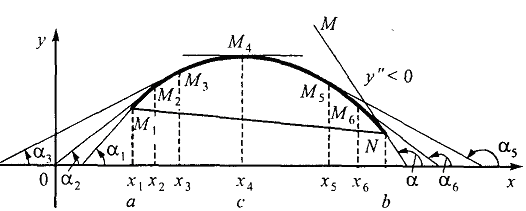
Непрерывная линия называется выпуклой или обра­щенной выпуклостью вверх на отрезке [а, b], если все точки этой линии ле­жат выше хорды, соединяющей любые две ее точки.

Вогнутой (обращенной выпуклостью вниз) называет­ся линия, проходящая ниже своих хорд.

Замечание. В некоторых руководствах выпуклость и вогнутость иногда определяются противоположным образом.

Точки, отделяющие выпуклые участки линии от вогнутых (и наоборот), называются точками перегиба.

На рисунках проиллюстрирован гео­метрический смысл второй производной, позволяющий по ее знаку судить о том, в какую сторону изгибается линия графика, т. е. справедлива

Теорема. Если вторая произ­водная функции 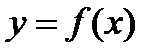в данном промежутке значений х положи­тельна:

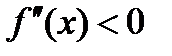(2.10),

то кривая вогнута в этом промежутке, а если отрицательна:

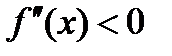(2.11),

то кривая в этом промежутке выпукла.

Точками перегиба являются те точки, при переходе через которые вторая производная меняет знак.

Линия является выпуклой(или вогнутой) в точке, если значение ее второй производной в данной точке меньше (или больше) нуля.

Пример.2.9.Выяснить, выпуклая или вогнутая линия 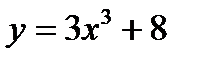при .

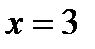Решение.Находим производные 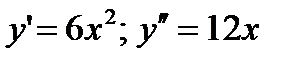. В точке 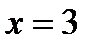имеем: 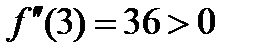. Значит, в точке 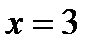данная линия вогнута.

Нахождение точки перегиба.Чтобы исследовать функцию на вогнутость, необходимо опреде­лить знак второй производной. Если на данном промежутке f"(х) < 0 для всех х, то линия вогнута, если f"(х) > 0 для всех х, то линия выпукла. Выпуклую часть кривой от вогнутой отделяет точка перегиба.

Чтобы найти точку перегиба линии :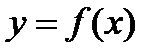

1. Найти вторую производную функции .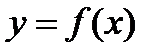

2. Приравняв ее к нулю, решить полученное уравнение.

3. Расположив корни второй производной 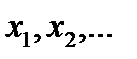. в порядке возрастания, подставить в выражение для второй производной сначала лю­бое число, меньшее 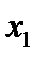, затем - любое число 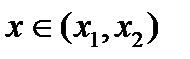; если получатся разные знаки, то при 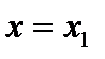имеется точка перегиба; если же одинаковые, то точки перегиба нет; далее аналогично поступить с числами .

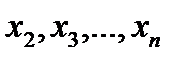4. Найти ординаты точек пе­региба, т. е. найти значения функ­ции в соответствующих точках.

Пример 2.10. Найти точки перегиба линии .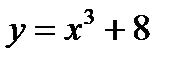

Решение. Находим: .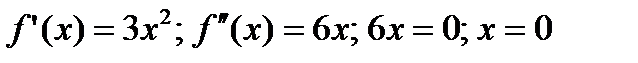

Разобьем числовую прямую на интервалы: ; .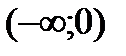

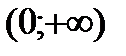Определим знак второй производной в каждом из интервалов.

x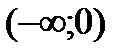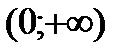
	-	+
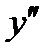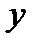	выпуклая	вогнутая

При переходе через 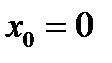вторая производная меняет знак на противоположный, следовательно, при 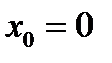линия имеет перегиб.

Ординату точки перегиба определим, подставив 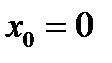в уравнение линии: 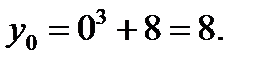Следовательно, 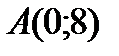- точка перегиба.

Пример 2.11.Найти точки пере­гиба линии .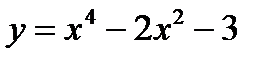

Решение.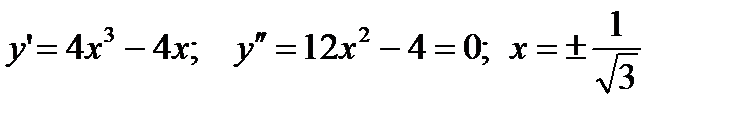

То есть, вторую производную можно разложить на множители:

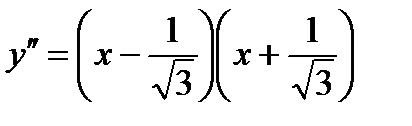
Разобьем числовую прямую на интервалы:

;

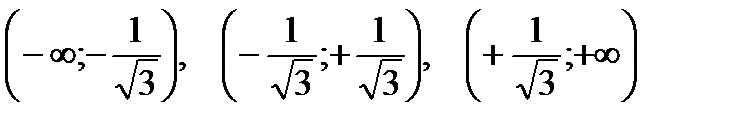Определим знак второй производной в каждом из интервалов. В результате определим участки выпуклости-вогнутости функции.

x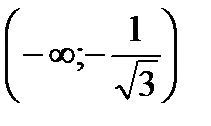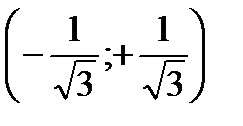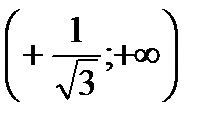
	+	-	+
y	вогнутая	выпуклая	вогнутая

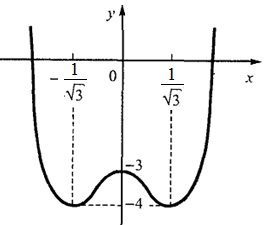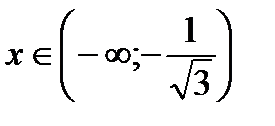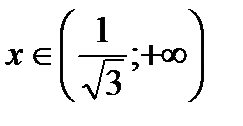При и имеем 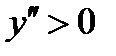- линия вогнута;

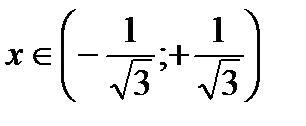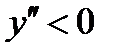при имеем - линия выпукла.

Точки 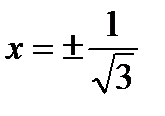являются точками перегиба (см.рис.)

Рассмотрим последовательность выполнения операций при исследовании функции и построении ее графика на следующем примере.

Пример 2.12. Исследуйте функцию и постройте ее график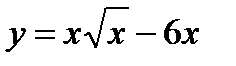

Решение.

1) Область определения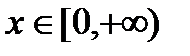

2) Функция не периодическая

3) Функция общего свойства, то есть не относится ни к четным, ни к нечетным.

3) Области возрастания-убывания.

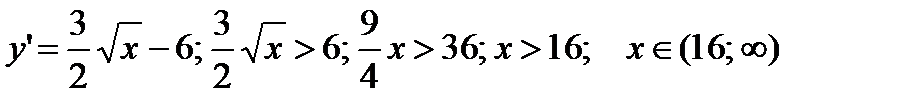- функция возрастает;

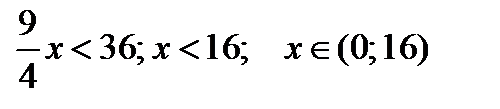- функция убывает.

4) Точки экстремумов: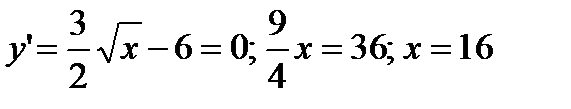

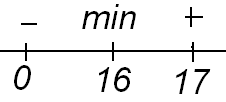
При 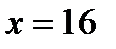имеем минимум. Для определения значения этого минимума подставим 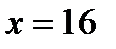в уравнение кривой: 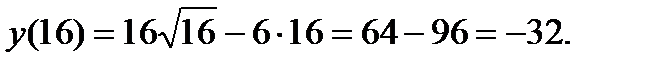Таким образом, у графика функции имеется точка минимума с координатами (16; -32).

5) Точки пересечения с осями координат.

Для определения ординаты точки пересечения с осью 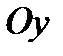подставим в уравнение кривой 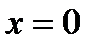. В результате получим: .

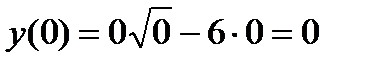Таким образом, график функции пересекает ось 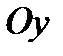при .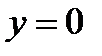

Для определения абсциссы точки пересечения с осью 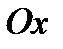подставим в уравнение кривой 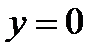. В результате получим:

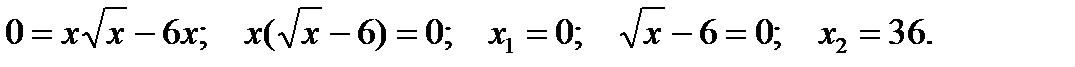
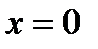Таким образом, график функции пересекает ось в двух точках: при и .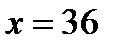

6) Области выпуклости-вогнутости.

Для определения участков вогнутости решаем неравенство: 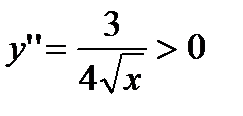. Оно справедливо для любого 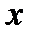из области определения. Следовательно, график функции всюду вогнут.

Для определения участков выпуклости решаем неравенство: 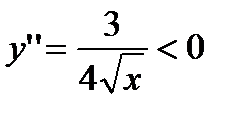. Оно не имеет решения. Следовательно, график функции не имеет участков выпуклости.

7) Точки перегиба:

Для определения точек перегиба решаем уравнение: 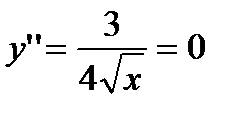. Оно не имеет решения. Следовательно, график функции не имеет точек перегиба.

8) Для построения графика функции начертим оси координат и отметим выявленные нами точки: минимума (16; -32) и пересечения с осями координат (0; 0) и (36; 0), а также области возрастания-убывания функции и ее вогнутости. В р 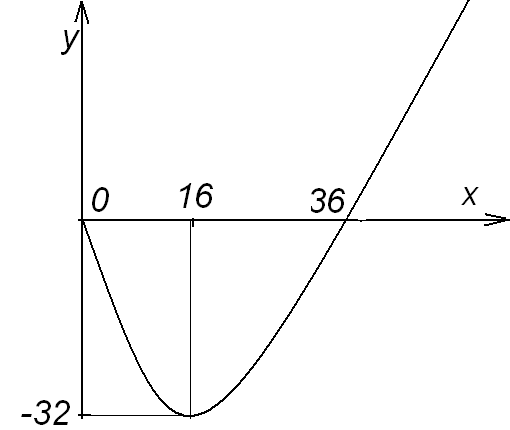езультате получим график, изображённый на рисунке.

Дифференциал функции.

Пусть функция у=ƒ(х) имеет в точке х отличную от нуля производную 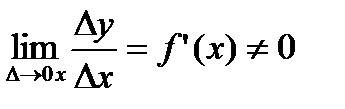. Тогда, по теореме о связи функции, ее предела и бесконечно малой функции, можно записать

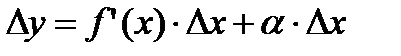, (2.12)

где α→0 при ∆х→0.

Таким образом, приращение функции ∆у представляет собой сумму двух слагаемых: 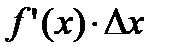и 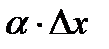, являющихся бесконечно малыми при ∆x→0. При этом первое слагаемое есть бесконечно малая функция одного порядка с ∆х, так как 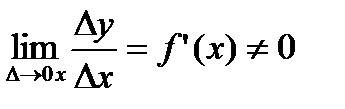а второе слагаемое есть бесконечно малая функция более высокого порядка, чем ∆х:

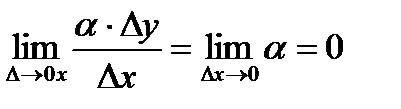. (2.13)

Поэтому первое слагаемое 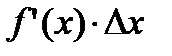называют главной частью приращения функции ∆y. Дифференциалом функции 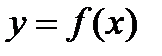в точке х называется главная часть ее приращения, равная произведению производной функции на приращение аргумента, и обозначается 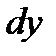(или ):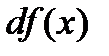

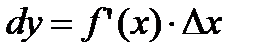(2.14)

Дифференциал 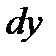называют также дифференциалом первого порядка. Найдем дифференциал независимой переменной х, т. е. дифференциал функции .

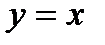Так как 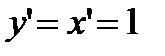, то, согласно формуле (2.1), имеем 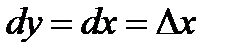, т. е. дифференциал независимой переменной равен приращению этой переменной:

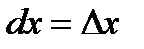. (2.15)

Поэтому формулу (2.14) можно записать так:

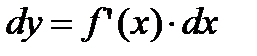, (2.16)

иными словами, дифференциал функции равен произведению производной этой функции на дифференциал независимой переменной.

Из формулы (2.16) следует равенство

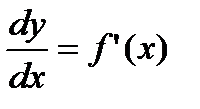. (2.17)

Теперь обозначение производной 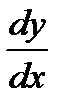можно рассматривать как отношение дифференциалов 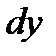и .

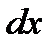Пример 2.13

Найти дифференциал функции .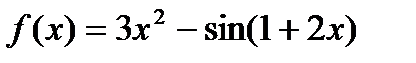

Решение:

По формуле 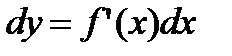находим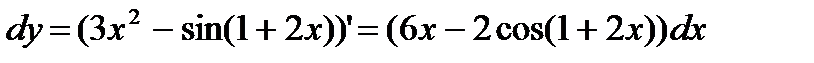

Пример 2.14. Найти дифференциал функции 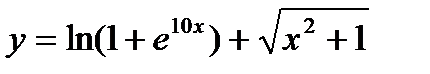. Вычислить 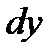при .

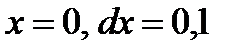Решение: .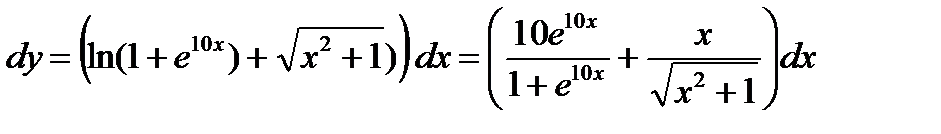

Подставив 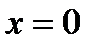и 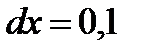, получим .

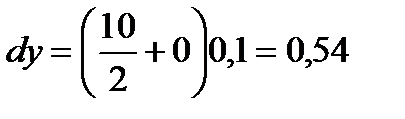Решение.

а)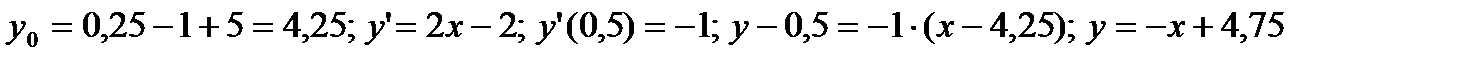

б)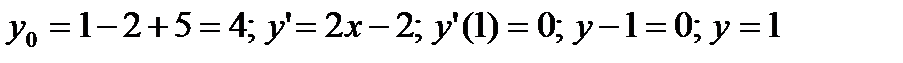

в)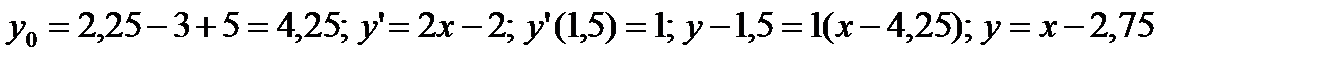

Пример 2.20. Определите углы, под которыми синусоида и тангенсоида пересекают ось абсцисс.

Решение.

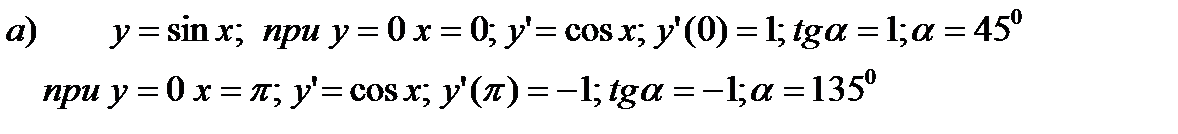
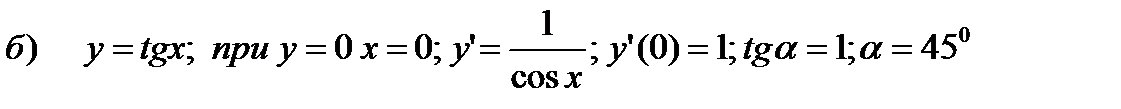
Пример 2.21. Под каким углом синусоида пересекает прямую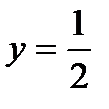

Решение. 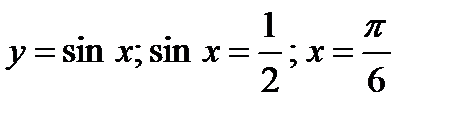- абсцисса точки пересечения синусоиды и прямой.

Координаты точки пересечения .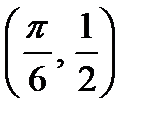

Определим углы наклона касательных с графиком функций в названных точках.

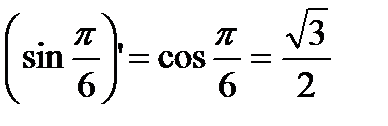- тангенс угла наклона синусоиды к оси x. Поскольку прямая параллельна этой оси, то 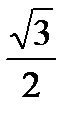является тангенсом угла между этой прямой и синусоидой. Таким образом, .

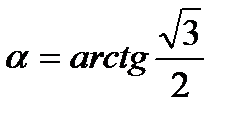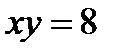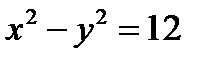Пример 2.22. Докажите, что гиперболы и пересекаются под прямым углом.

Решение.

1) Определим координаты точки пересечения гипербол.

Из первого уравнения: 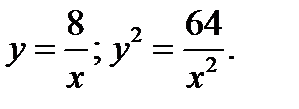Из второго уравнения 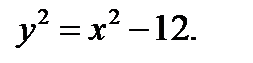Таким образом, получим: .

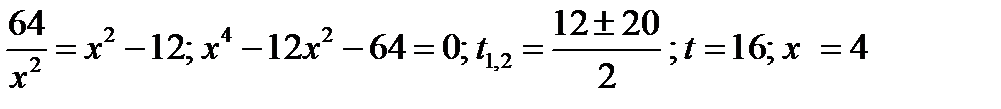Таким образом, ордината точки пересечения гипербол равна 2. Определим углы наклона к оси x касательных к каждой из гипербол в указанной точке.

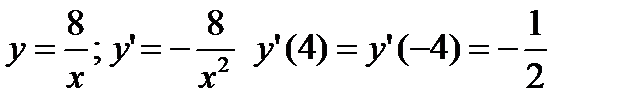- первая гипербола .

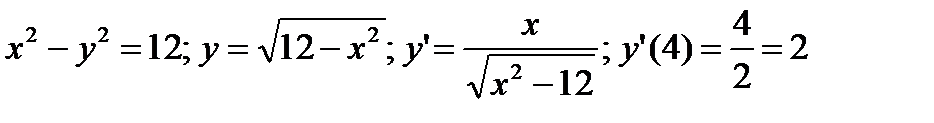- вторая гипербола .

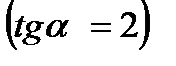Получили: 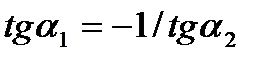, что является признаком перпендикулярности касательных, а, значит, и гипербол.

Пример 2.23. Определите угол, под которым пересекаются лини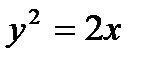и

и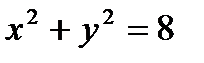

Решение.

1) Ордината точки пересечения: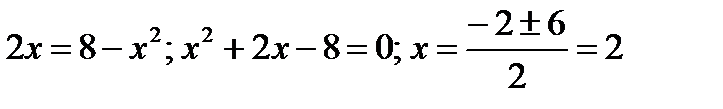

2) Углы наклона касательных к оси x:

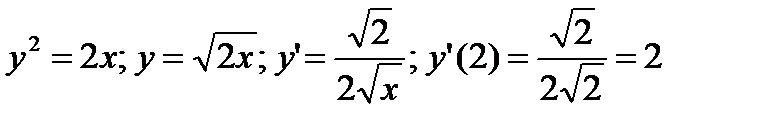- для линии .

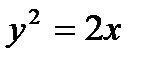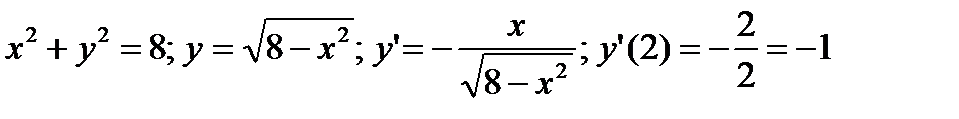- для линии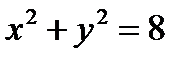

Угол между двумя прямыми определяется формулой: ;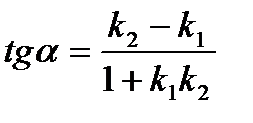

;

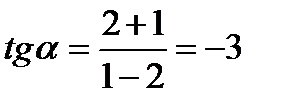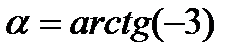
Пример 2.24. Составьте уравнения касательных к линии 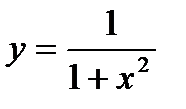в точках ее пересечения с гиперболой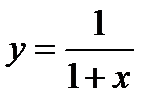

Решение

1) Точки пересечения линий

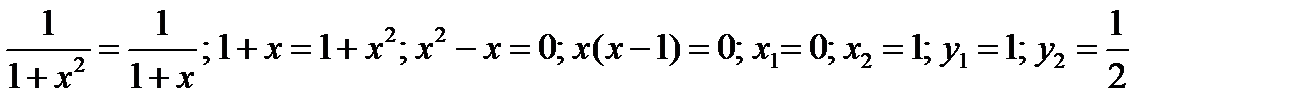
2) Угол наклона к оси x касательной к кривой 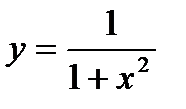в точке :

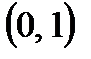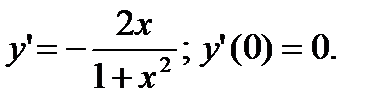
Уравнение касательной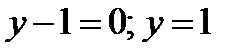

Угол наклона к оси x касательной к кривой 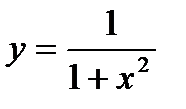в точке :

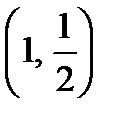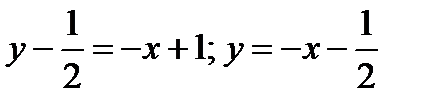
Пример 2.25. Составьте уравнения прямых, проходящих через точку 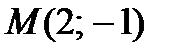и касающихся линии .

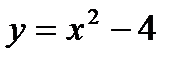Решение. Точка M(2;-1) не является точкой касания, так как .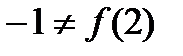

Уравнение касательной, проходящей через точку с абсциссой 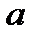, имеет следующий вид: .

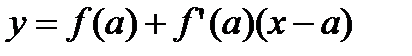Определим значение .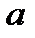

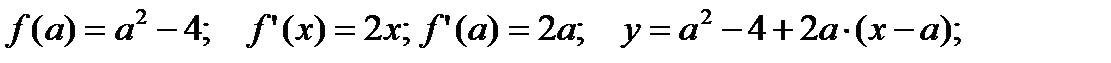
Касательная проходит через точку M (2;-1), следовательно, ее координаты удовлетворяют уравнению касательной.

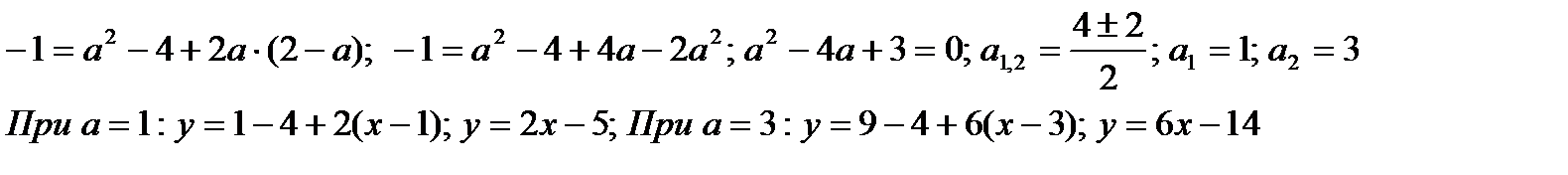
Пример 2.26. Составьте уравнение касательной к линии 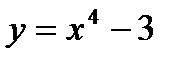, проходящей через точку .

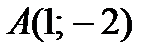Решение. Точка A(2;-1) является точкой касания, так как .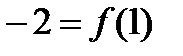

Уравнение касательной имеет следующий вид: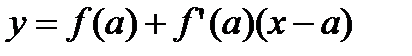

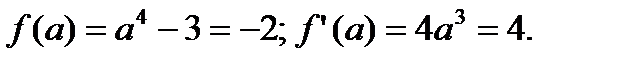
Таким образом, имеем: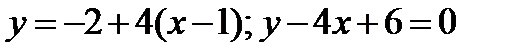

Пример 2.27. Составить уравнение касательной и нормали, прове­денных к кривой 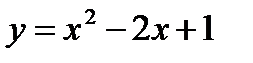в точке, абсцисса которой равна 2.

Решение. Найдем ординату точки касания: 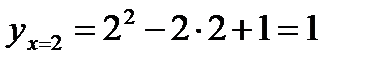. Точка касания 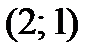. Уравнение касательной 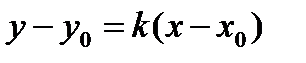;уравнение нормали 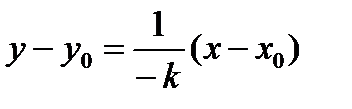, где 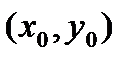- координаты точки касания; k - угловой коэффициент касательной: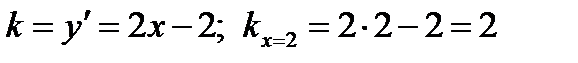

Уравнение искомой касательно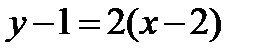й: или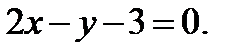

Уравнение норма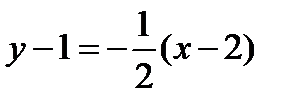ли: или .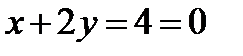

2.6. Механический смысл производной.

Если закон прямолинейного движения точки задан уравнением 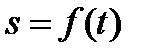, где s - путь; t - время, то мгновенная скорость движения v в момент t определяется равен­ствами

,

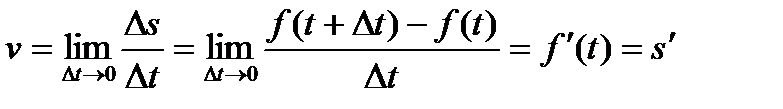т. е. скорость точки при прямолинейном движении в момент време­ни t есть производная от пути s по времени.

Ускорение точки при прямолинейном движении в момент време­ни t есть производная от пути v по времени или вторая производная от пути s по времени.

Пример 2.28. Точка движется прямолинейно по закону 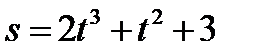. Найти скорость и ускорение в момент ,

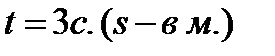Решение.

Находим скорость

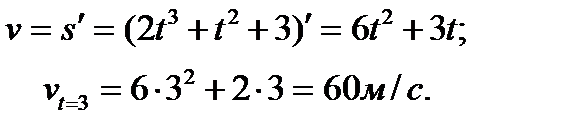
Находим ускорение

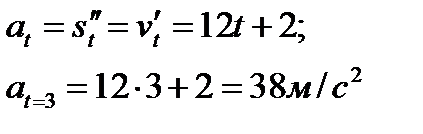
ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ

Методы интегрирования

I. Непосредственное интегрирование.

Этот способ интегрирования предполагает такое преобразование подынтегральной функции, которое позволило бы использовать для ре­шения табличные интегралы.

Пример 3.3. Найти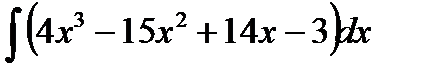

Решение.Воспользуемся свойством 2. интеграла: интеграл от суммы (разности) функций равен сумме (разности) интегралов от этих же функций.

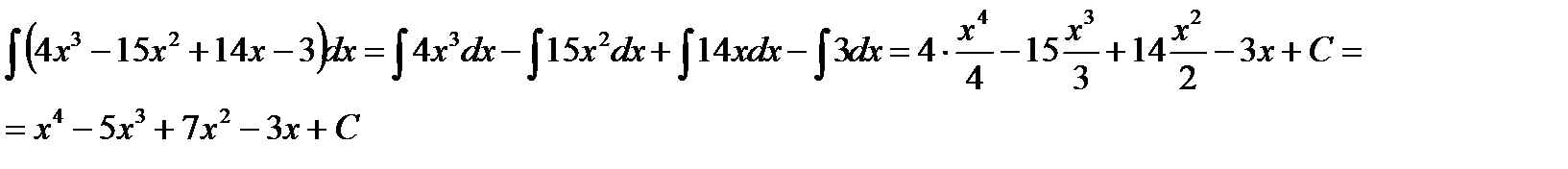
Пример 3.4.Найти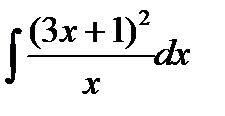

Решение.Приведем интеграл к табличному виду. Для этого раскроем скобки в числителе и разделим почленно числитель на знаменатель.

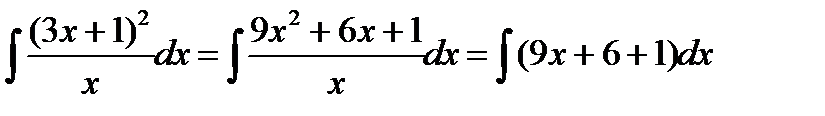
Затем воспользуемся указанным выше свойством интеграла суммы (разности) функций: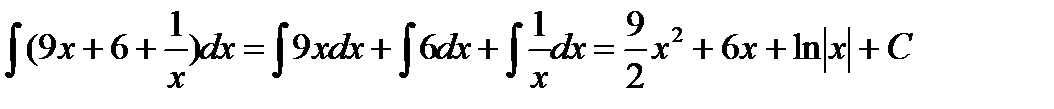

II.Метод подстановки.

Этот метод называют также методом замены переменной. Использование этого метода основано на свойстве 3 интеграла.

Пример 3.5. Найти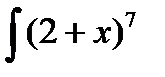

Решение.Введем новую переменную: .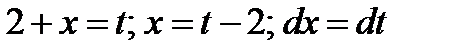

Найдем интеграл: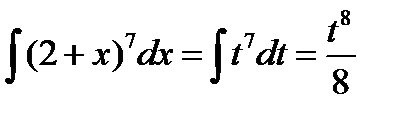

Выразим результат через первоначальный аргумент: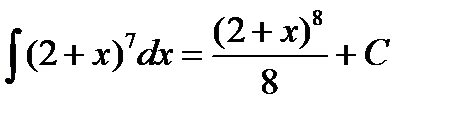

Пример 3.6.Найти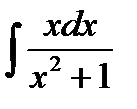

Решение. Сделаем подстановку 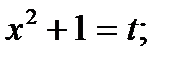Надо определить, чему равен dx. Для этого продифференцируем выражение 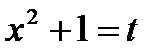, в результате чего получим .

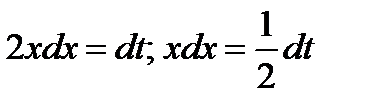Подставим все это в первоначальный интеграл, в результате чего будем иметь:

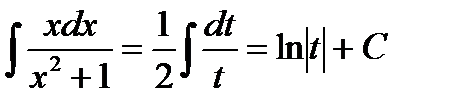
Выразим результат через первоначальный аргумент: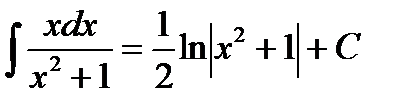

Этот пример дает возможность сделать следующий общий вывод: .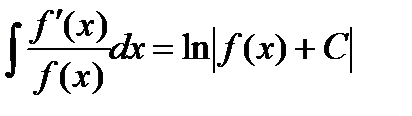

III. Метод интегрирования по частям.

Использование этого метода основано на свойстве (4) интеграла: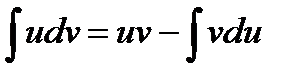

Пример 3.7. Найти .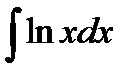

Решение. Обозначим .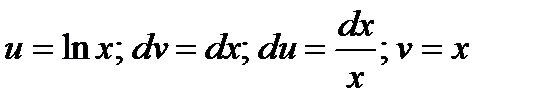

Подставим полученные данные в первоначальное выражение:

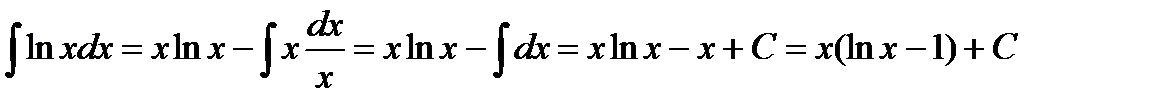
Пример 3.8. Найти .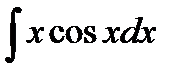

Решение.Интегрируем по частям

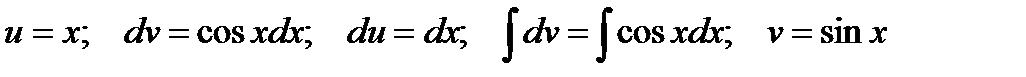
Тогда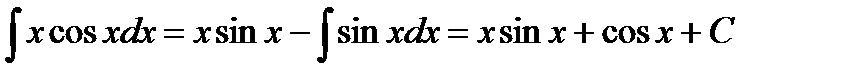

Пример 3.9. Найти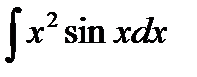

Решение.Интегрируем по частям

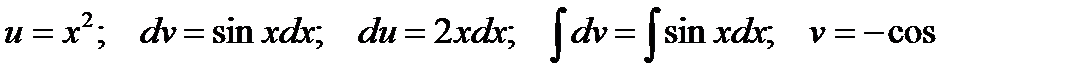
Тогда .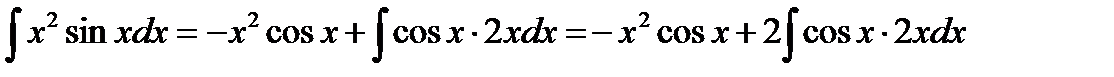

Подставим значение интеграла из примера 3.8, получим

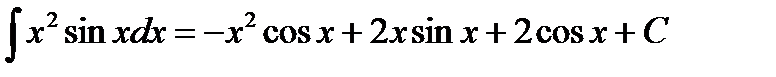
Решение

Так как плотность распределена неравномерно, то для наиболее точного ее нахождения разобьем весь стержень точками на 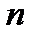достаточно малых частей (см. рис.)

Обозначим длину отрезка 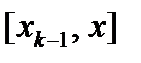через 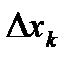. В силу того, что длины отрезков малы, в границах каждого из них плотность стержня можно считать постоянной и равной 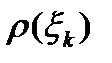, где 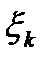- одна из точек k-го отрезка 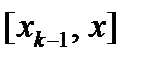. Тогда масса этого отрезка стержня равна 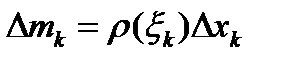. Масса всего стержня приближенно равна:

.

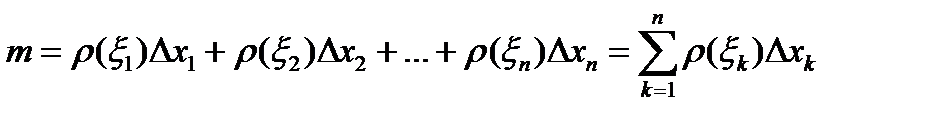При стремлении 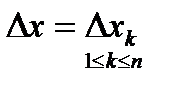к нулю, эта сумма стано­вится равной 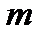, то есть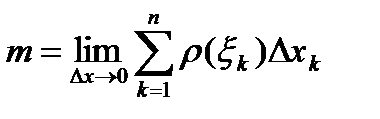

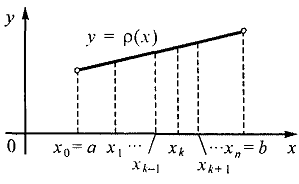
Задача о площади криволи­нейной трапеции. Дана плоская фи­гура, ограниченная графиком функ­ции 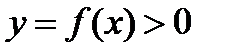и отрезками пря­мых 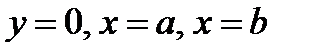. Функция 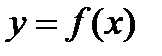определена, непрерывна и неотрицательна в промежутке [а, b]. Вычислить площадь S полученной фигуры (аАВb), называемой криволинейной трапецией.

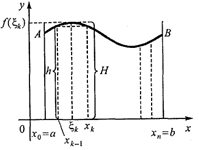Решение.Для того чтобы вычислить искомую площадь, разобьем промежуток [а, b] на nпроизвольных частей: 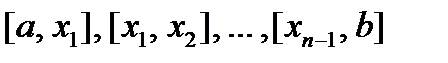, длины которых обозначим соответственно 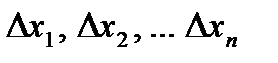. Через каждую точку деления проведем прямую, параллельную оси ординат. Эти прямые разделят данную фигуру на nполос. Заменим ка­ждую из этих полос прямоугольником, основание которого то же, что у полосы, а высота совпадает с одной из ординат точек графика функции в этой полосе.

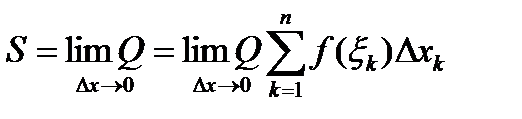
Обобщим рассуждения, проведенные при решении двух предыду­щих задач о массе прямолинейного стержня и о площади криволиней­ной трапеции. Пусть некоторая функция 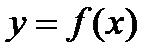задана на промежутке [а, b] и непрерывна. При разбиении промежутка [а, b] на n частей, та­ким образом, что максимальная длина отрезков разбиения стремится к нулю