Построение линейной регрессии

Данный раздел посвящён построению и исследованию уравнения линейной регрессии вида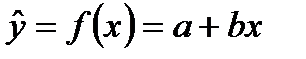

Построение линейной регрессии сводится к оценке ее параметров a, b.

Классический подход к оцениванию параметров линейной регрессии основан на методе наименьших квадратов (МНК).

Коэффициенты, определяемые на основе МНК, являются решением системы уравнений:

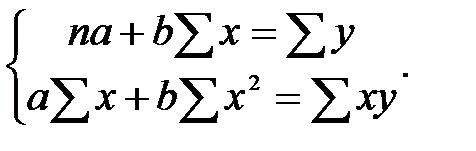
Решая эту систему уравнений, получим

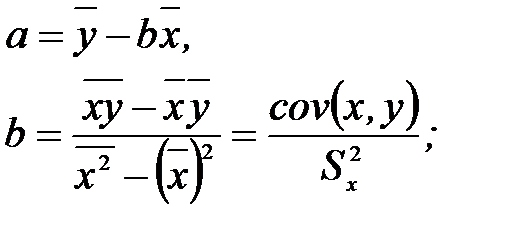
где cov(x, y)= 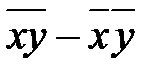– выборочная ковариация;

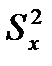– выборочное значение дисперсии величины x, определяемой по формуле:

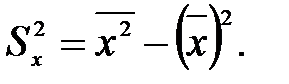
В вычислительной среде табличного процессора MS Excel эта задача (нахождение коэффициентов уравнения линейной регрессии) решается при помощи статистических функций НАКЛОН(наклон прямой относительно оси Х, коэффициент b) и ОТРЕЗОК(отрезок, отсекаемый прямой на оси Y, коэффициент a).

Статистическая функция КВПИРСОНвычисляет значение коэффициента детерминации.

Построение линейной и нелинейной регрессий с использованием команды «Добавить линию тренда»

Команда «Добавить линию тренда»используется для выделения тренда

(медленных изменений) при анализе временных рядов. Однако эту команду можно использовать и для построения уравнения нелинейной регрессии, рассматривая в качестве времени t независимую переменную x.

Эта команда позволяет построить следующие уравнения регрессии:

¾ линейная;

¾ полиноминальная;

¾ логарифмическая;

¾ степенная;

¾ экспоненциальная.

Для построения одной из перечисленных регрессий необходимо выполнить

следующие шаги:

Шаг 1. Ввести по столбцам исходные данные

Шаг 2. По этим данным построить график в декартовой системе координат

Шаг 3. Установить курсор на любую точку построенного графика, сделать

щелчок правой кнопкой и в появившемся контекстном меню выполнить

команду «Добавить линию тренда».

Шаг 4. В появившемся диалоговом окне выбрать нужное уравнение регрессии.

Шаг 5. «Включить» необходимые опции:

«Показать уравнение на диаграмме»– на диаграмме будет показано выбранное уравнение регрессии с вычисленными коэффициентами;

«Поместить на диаграмму величину достоверности аппроксимации (R²)»– на диаграмме будет показано значение коэффициента детерминации(для нелинейной регрессии индекс детерминации R²).

Если по построенному уравнению регрессии необходимо выполнить прогноз, то нужно указать число периодов прогноза.

Шаг 6. После задания всех перечисленных опций на диаграмме появится

формула построенного уравнения регрессии и значение индекса детерминации R².

Пример выполнения

Исходные данные

Шифр: 1210-п/СДс5681

Результаты измерения уровня помехи, для которых необходимо провести статистический анализ выборки, приведен в таблице 1.

Таблица 1. Результаты измерения уровня помехи

№ п/п
U, В	3,484	3,443	2,763	1,934	1,574	1,925	2,648	2,197	1,257	2,074
№ п/п
U, В	1,73	1,94	2,9	0,501	3,013	2,262	2,737	3,25	2,526	0,506
№ п/п
U, В	3,224	0,462	2,654	2,962	3,08	2,431	3,774	2,566	4,314	1,609
№ п/п
U, В	2,564	4,321	3,458	3,433	1,306	2,212	3,577	2,09	1,992	2,61

Результаты измерения зависимости напряжения сигнального тока от значения силы тока, на основании которых необходимо провести регрессионный анализ, приведены в таблице 2.

Таблица 2. Результаты измерения зависимости напряжения сигнального тока от силы тока

I, А	0,80	1,00	1,40	1,50	1,80	1,90	2,10	2,20	2,30
U, В	9,975	10,045	9,207	9,139	8,867	9,357	9,358	8,523	8,570
I, А	2,50	2,80	2,90	3,00	3,30	3,40	3,50	3,60	3,70
U, В	9,336	8,779	8,905	8,703	8,203	9,141	8,842	8,169	8,727
I, А	3,90	4,00	4,10	4,20	4,40	4,60	4,70
U, В	8,756	8,967	9,504	9,136	9,440	9,606	9,856

1 Статистический анализ случайной величины с использованием
табличного процессора