Определение закона распределения случайной величины

Закон распределения случайной величины – это соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями.

Закон распределения случайной величины характеризуется функцией и плотностью распределения.

Функция распределения – функция F(x), равная для каждого значения x вероятности того, что случайная величина X примет значение меньше x:

.

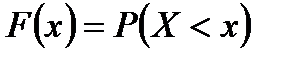Плотность распределения – это функция f(x), равная производной от функции распределения:

.

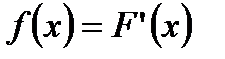Среди основных законов распределения случайной величины можно выделить следующие.

Равномерный закон распределения.

Пусть x – это случайное число, распределенное по равномерному закону в интервале (a, b). Тогда функция равномерного закона распределения имеет вид:

,

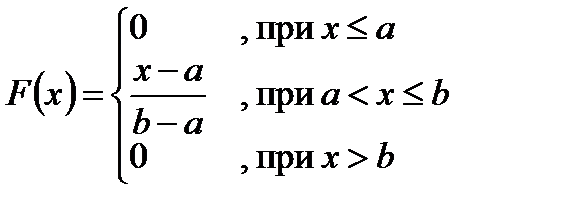Плотность равномерного закона распределения (рис. 1):

.

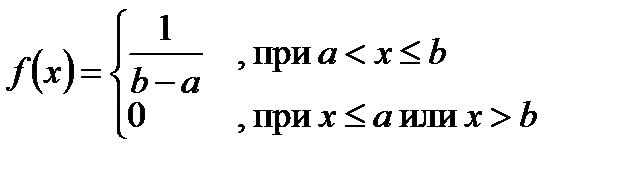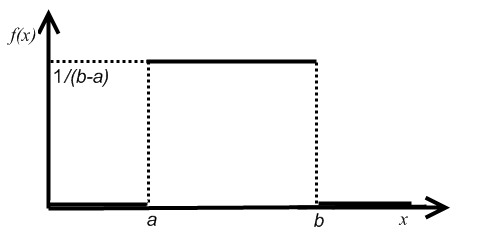
Рисунок 1. График плотности распределения вероятностей равномерной случайной величины

Нормальный закон распределения.

Функция нормального закона распределения имеет вид:

.

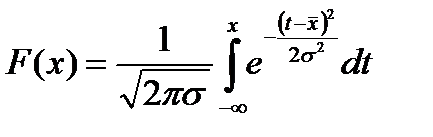Плотность нормального закона распределения (рис. 2):

.

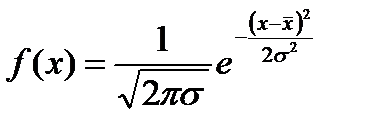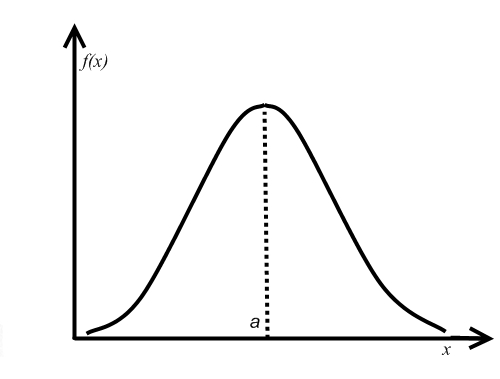
Рисунок 2. График плотности распределения вероятностей нормальной случайной величины

Экспоненциальный (показательный) закон распределения.

Функция экспоненциального закона распределения имеет вид:

,

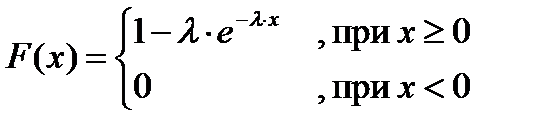где l – параметр экспоненциального распределения.

Плотность экспоненциального закона распределения (рис. 3):

.

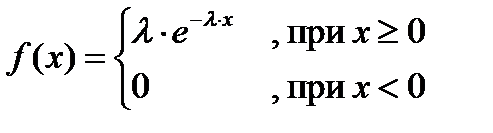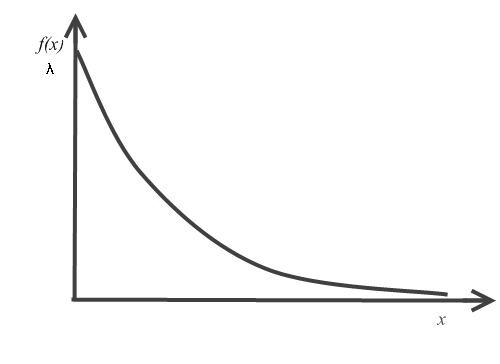
Рисунок 3. График плотности распределения вероятностей экспоненциальной случайной величины

Чтобы сделать предположение о том, к какому закону распределения относится выборка случайной величины, можно использовать график частоты выборочного значения, который при достаточном объеме выборки по характеру совпадает графиком плотности распределения вероятности случайной величины. Построение графика или гистограммы частоты выборочного значения производится с помощью функции табличного процессора MS Excel «Гистограмма». Вызов данной функции выполняется во вкладке панели быстрого доступа «Данные», в разделе «Анализ», далее кнопка «Анализ данных». В появившемся окне необходимо выбрать пункт «Гистограмма». В графе «Входной интервал» требуется указать диапазон округлённых значений оцениваемых случайных величин. Для получения значений округлённых значений случайных величин необходимо воспользоваться функцией =ОКРУГЛ(число; число разрядов). В графе «Интервал карманов» указывается диапазон содержащий перечень различных округлённых значений оцениваемых случайных величин. «Выходной интервал» – интервал ячеек предназначенных для вывода результата функции «Гистограмма». Так же необходимо поставить галочку в пункте «Вывод графика».

Проверка гипотезы о виде распределения выборки случайной величины производится по критерию Пирсона. Сначала формулируются нулевая (Н0) и альтернативная (Н1) гипотезы. Гипотеза Н0 – это гипотеза о том, что выборка случайной величины подчиняется предполагаемому закону распределения. Гипотеза Н1 – это гипотеза о том, что выборка случайной величины не подчиняется предполагаемому закону распределения.

Используя уровень значимости равный 0,05, критическое значение χ² статистики (критерий Пирсона) определяется по формуле:

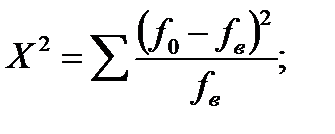
где f₀ – наблюдаемая частота,

f_в – теоретическая, или ожидаемая частота.

Решающее правило формулируется следующим образом: гипотеза Н0 отклоняется, если 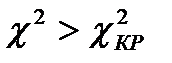, в противном случае гипотеза Н0 не отклоняется.

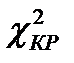– это табличное значение критерия, которое берётся в соответствии с заданными значениями уровня значимости, количества степеней свободы и количества оцениваемых параметров.

Чтобы провести проверку гипотезы о виде распределения выборки случайной величины по критерию Пирсона с использованием табличного процессора MS Excel выполняется следующая последовательность действий.

Сначала производится вычисление n_i (частоты выборочных значений x_i). Это возможно сделать воспользовавшись функцией =СЧЁТЕСЛИ(диапазон проверяемых значений; критерий по которому производится проверка).

Затем требуется вычислить значение теоретической вероятности p_i. Проверка гипотез о равномерном, нормальном или экспоненциальном распределении отличается формулой вычисления p_i.

Для проверки гипотезы о равномерном распределении значение теоретической вероятности p_i вычисляется по формуле: 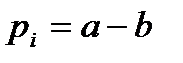. Параметры равномерного распределения a и b являются решением системы уравнений:

.

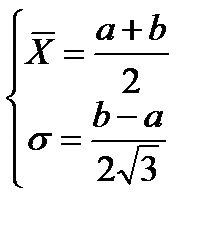Для проверки гипотезы о нормальном распределении используется функция =НОРМРАСП(x_i; 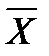; σ; 1).

Для проверки гипотезы об экспоненциальном распределении используется функция =ЭКСПРАСП(x_i; l; 1),

где l - параметр экспоненциальной функции, вычисляется по формуле:

.

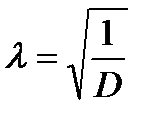Вычисляется теоретическая частота выборочного значения x_i по формуле:

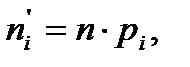
где n – количество наблюдений, объём выборки.

Затем вычисляется наблюдаемое значение случайной величины:

.

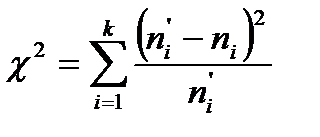Для упрощения написания формулы в табличном процессоре процесс вычисления формулы для вычисления наблюдаемого значение случайной величины возможно разделить на два действия: деление и сумма результатов деления.

Критическое значение случайной величины χ² возможно определить с помощью функции

χ²_кр=ХИ2ОБР(a, r)

где a – уровень значимости, требуемая вероятность, которая принимается равной значению 0,05;

r – количество степеней свободы.

Расчет количества степеней свободы производится по формуле:

,

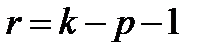где k – количество категорий (количество различных округлённых значений),

р – количество оцениваемых параметров закона распределения.

Если проводиться проверка гипотезы о нормальном распределении случайной величины, то количество оцениваемых параметров (p) равно 2 (средние арифметическое и среднее квадратическое отклонение выборки). Если проводиться проверка гипотезы о равномерном распределении случайной величины, то p также равно 2 (параметры a и b). При проверке гипотезы об экспоненциальном распределении случайной величины p = 1 (параметр l).

Сравнив χ²_кр и χ² можно сделать вывод о значимости гипотезы: если χ²_кр > χ², то гипотеза принимается с уровнем значимости a, в противном случае гипотеза отвергается.