Основные свойства функции Гаусса

1. Немецкий математик К.Ф.Гаусс в 1821 г. получил формулу нормального распределения значений случайной величины:

.

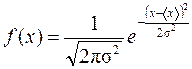Функция 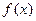называется плотностью вероятности и равна числу значений, приходящихся на единичный интервал значений случайной величины. Соответственно, 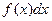равно числу попаданий значений случайной величины 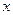в интервал от 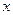до .

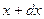2. Кривая нормального распределения является симметричной относительно вертикальной оси, проходящей через ее максимум, т.е. одинаковые отклонения значений, но в противоположные стороны встречаются одинаково часто и имеют одинаковую вероятность.

3. В точке 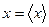функция 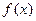имеет максимум, т.е. среднее арифметическое значение 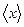случайной величины является наиболее вероятным (рис. 3).

4. Площадь под кривой 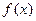должна быть равна 1, так как выражает вероятность достоверного события (т.е. значение 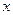случайной величины обязательно находится на числовой оси).

5. Точки a и b являются точками перегиба функции 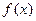, в которых .x₁ = <x> – σ и x₂ = <x> + σ

Доля всех значений случайной величины, попадающих в интервал (–σ, +σ) составляет 68,3%. В интервале (–2σ, +2σ) находится 95,4% всех значений, а для интервала (–3σ, +3σ) эта доля соответственно уже 99,9%.

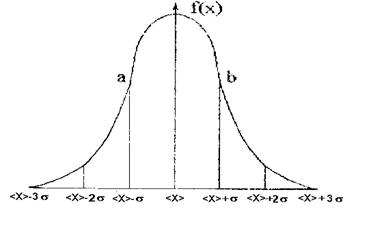
Рис. 3. Кривая нормального распределения значений

случайной величины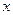

Величина 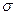называется средним квадратичным отклонением, а σ² – дисперсией, характеризующей рассеяние значений случайной величины (dispersio – рассеяние) относительно ее среднего значения. При уменьшении σ кривые распределения будут иметь иглообразный максимум, а при увеличении σ, наоборот, пологий, размытый.

Площади под кривой, ограниченные этими интервалами (их также называют доверительными интервалами), равны вероятности попадания значения случайной величины внутрь интервала. Эта вероятность называется доверительной вероятностью (надежностью) (рис. 4).

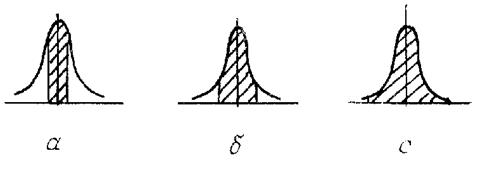
Рис. 4. Доверительные интервалы Δx_a = σ, Δx_b = 2σ, Δx_c = 3σ;

доверительные вероятности, соответственно, равны:

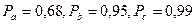
В теории погрешности случайной величиной является результат измерения (а также погрешность измерения).

Абсолютной погрешностью измерения называется величина, определяемая разницей между результатом измерения 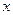и действительным значением измеряемой величины :

.

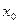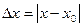Относительной погрешностью называется величина, равная отношению абсолютной погрешности к среднему арифметическому значению результата измерения,

.

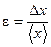Теперь вспомним то обстоятельство, что экспериментатор имеет дело с ограниченным числом измерений, часто незначительным. При этом распределение случайных погрешностей тем больше отличается от нормального распределения, чем меньше сделано измерений.

Английский химик и математик У. Госсет (1908), публиковавший свои работы под псевдонимом Стьюдент (Student), указал на возможность и при малом числе измерений определять доверительный интервал. Он вывел распределение погрешностей, получаемых при малом числе измерений (малой выборке). Кривые распределения Стьюдента (рис. 5) по своей форме напоминают кривую Гаусса, и при числе измерений 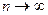средняя квадратичная погрешность 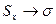, а распределение Стьюдента сближается с нормальным распределением.

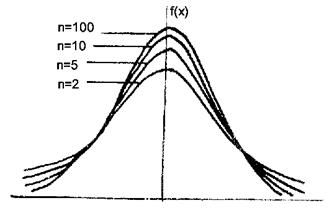
Рис. 5. Кривые распределения Стьюдента

для различного числа измерений

По Стьюденту, центр доверительного интервала определяется средним арифметическим значением, полученным из 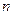измерений:

.

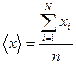Абсолютная погрешность измерения равна полуширине доверительного интервала для заданной надежности измерения α и определяется соотношением

,

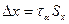где 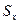– среднее квадратичное отклонение.

,

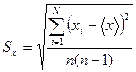где τ_α – коэффициент Стьюдента, учитывающий количество измерений n и требуемую надежность α. Значения коэффициентов Стьюдента приводятся в таблицах.

После определения погрешности методом Стьюдента результат прямых измерений записывают в стандартном виде

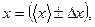(единица измерения)

при α = 0,95

.

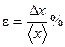Надежность измерений (доверительная вероятность) α для научных и инженерных измерений принята равной 95%.

При расчете погрешностей, сопровождающих косвенные измерения, используют следующий алгоритм. Пусть, например, измеряемая величина 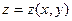является функцией величин 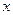и 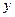, которые измеряются прямым методом. Тогда среднее значение найдем по средним значениям 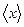и 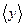в соответствии с выражением .

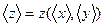А погрешность 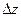найдем по формуле ,

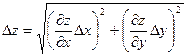где 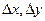– погрешности прямых измерений величин ;

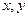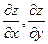– частные производные функции .

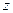Определение числа π методом Бюффона

В качестве примера рассмотрим предложенный Бюффоном эксперимент для определения числа π (игла Бюффона).

Возьмите миллиметровую бумагу или лист тетради в клетку. Сторона клетки (квадрата) – 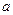. На этот лист случайным образом бросайте иглу, спичку, спицу и т.п. длиной L (L > 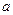). Число линий, которые пересечет или коснется игла в каждом бросании, обозначим m_i (рис. 6). Число π вычисляется по формуле

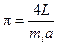
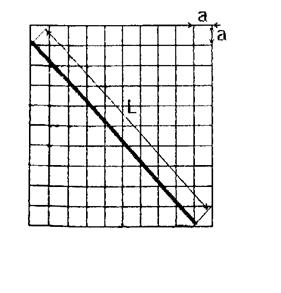
Рис. 6. 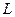– размер «иглы», а – размер стороны клетки