Метод обратного распространения ошибки
Этот метод обучения многослойной нейронной сети называется обобщенным дельта-правилом или правилом errorbackpropagation (обратного распространения ошибки). Метод был предложен в 1986г. Руммельхартом, Маклеландом и Вильямсом [89]. Это ознаменовало возрождение интереса к нейронным сетям, который стал угасать в начале 70-х годов. Позже было обнаружено, что Паркер опубликовал подобные результаты в 1982г., а Вербос выполнил такую работу в 1984г. Однако такова природа науки, что ученые, работающие независимо друг от друга, не могут использовать все то прогрессивное, что есть в других областях, и поэтому часто случается повторение уже достигнутого. Однако статья Руммельхарта и др., опубликованная в журнале Nature (1986), является до сих пор наиболее цитируемой в этой области [81].
Обучение сети начинается с предъявления образа и вычисления соответствующей реакции (рис. 6.5.). Сравнение с желаемой реакцией дает возможность изменять веса связей таким образом, чтобы сеть на следующем шаге могла выдавать более точный результат. Обучающее правило обеспечивает настройку весов связей. Информация о выходах сети является исходной для нейронов предыдущих слоев. Эти нейроны могут настраивать веса своих связей для уменьшения погрешности на следующем шаге. Когда мы предъявляем ненастроенной сети входной образ, она будет давать некоторый случайный выход. Функция ошибки представляет собой разность между текущим выходом сети и идеальным выходом, который необходимо получить. Для
успешного обучения сети требуется приблизить выход сети к желаемому выходу, т.е. последовательно уменьшать величину функции ошибки. Это достигается настройкой межнейронных связей. Обобщенное дельта-правило обучает сеть путем вычисления функции ошибки для заданного входа с последующим ее обратным распространением (вот откуда название) от каждого слоя к предыдущему. Каждый нейрон в сети имеет свои веса, которые настраиваются, чтобы уменьшить величину функции ошибки. Для нейронов выходного слоя известны их фактические и желаемые значения выхода. Поэтому настройка весов связей для таких нейроновявляется относительно простой. Однако для нейронов предыдущих слоев настройка не столь очевидна. Интуитивно ясно, что нейроны внутренних слоев, которые связаны с выходами, имеющими большую погрешность, должны изменять свои веса значительно сильнее, чем нейроны, соединенные с почти корректными выходами. Другими словами, веса данного нейрона должны изменяться прямо пропорционально ошибке тех нейронов, с которыми данный нейрон связан. Вот почему обратное распространение этих ошибок через сеть позволяет корректно настраивать веса связей между всеми слоями. В этом случае величина функции ошибки уменьшается и сеть обучается.
Основные соотношения метода обратного распространения ошибки получены в [81] при следующих обозначениях:
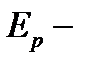 величина функции ошибки для образа
величина функции ошибки для образа 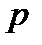 ;
;
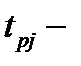 желаемый выход нейрона
желаемый выход нейрона 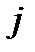 для образа
для образа 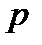 ;
;
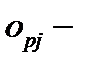 действительный выход нейрона
действительный выход нейрона 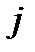 для образа
для образа 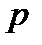 ;
;
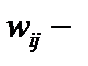 вес связи между
вес связи между 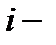 м и
м и 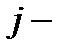 м нейронами.
м нейронами.
Пусть функция ошибки прямо пропорциональна квадрату разности между действительным и желательным выходами для всей обучающей выборки:
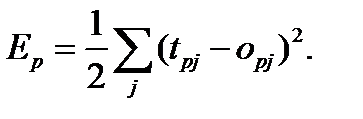 (6.1)
(6.1)
Множитель 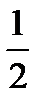 вводится здесь для упрощения операции дифференцирования.
вводится здесь для упрощения операции дифференцирования.
Активация каждого нейрона 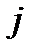 для образа
для образа 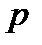 записывается в виде взвешенной суммы:
записывается в виде взвешенной суммы:
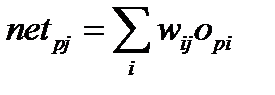 . (6.2)
. (6.2)
Выход каждого нейрона 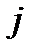 является значением пороговой функции
является значением пороговой функции 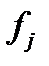 , которая активизируется взвешенной суммой. В многослойной сети это обычно переходная функция, хотя может использоваться любая непрерывно дифференцируемая монотонная функция:
, которая активизируется взвешенной суммой. В многослойной сети это обычно переходная функция, хотя может использоваться любая непрерывно дифференцируемая монотонная функция:
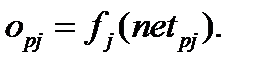 (6.3)
(6.3)
Тогда можно будет записать по правилу цепочки:
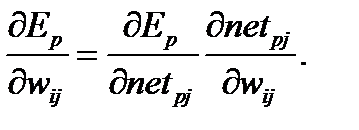 (6.4)
(6.4)
Для второго сомножителя в (6.4), используя (6.2), получаем:
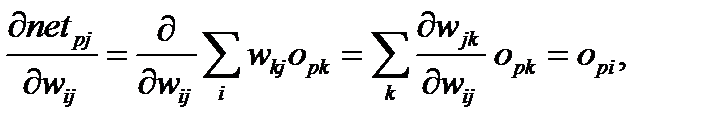 (6.5)
(6.5)
поскольку 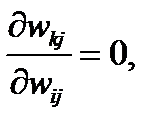 за исключением случая
за исключением случая 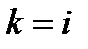 , когда эта производная равна единице.
, когда эта производная равна единице.
Изменение ошибки как функция изменения входов нейрона определяется так:
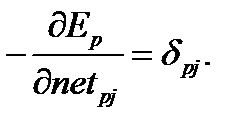 (6.6)
(6.6)
Поэтому (6.4) преобразуется к виду:
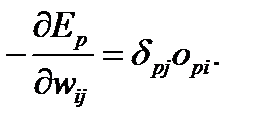 (6.7)
(6.7)
Следовательно, уменьшение величины 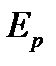 означает изменение веса пропорционально
означает изменение веса пропорционально 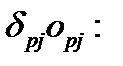
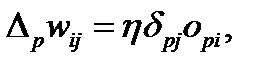 (6.8)
(6.8)
где 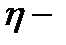 коэффициент пропорциональности, влияющий на скорость обучения.
коэффициент пропорциональности, влияющий на скорость обучения.
Теперь нам необходимо знать значение 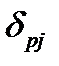 для каждого нейрона. Используя (6.6) и правило цепочки, можно записать:
для каждого нейрона. Используя (6.6) и правило цепочки, можно записать:
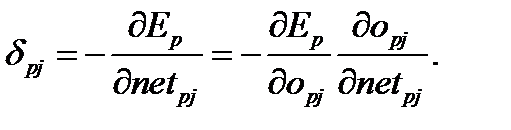 (6.9)
(6.9)
Исходя из (6.3), записываем второй сомножитель в (6.8):
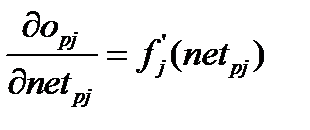 . (6.10)
. (6.10)
Теперь рассмотрим первый сомножитель в (6.9). Согласно (6.1), нетрудно получить:
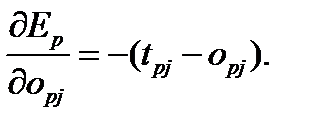 (6.11)
(6.11)
Поэтому 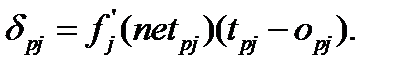 (6.12)
(6.12)
Последнее соотношение является полезным для выходных нейронов, поскольку для них известны целевые и действительные значения выходов. Однако для нейронов внутренних слоев целевые значения выходов не известны.
Таким образом, если нейрон 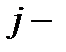 не выходной нейрон, то снова, используя правило цепочки, а также соотношения (6.2) и (6.6), можно записать:
не выходной нейрон, то снова, используя правило цепочки, а также соотношения (6.2) и (6.6), можно записать:
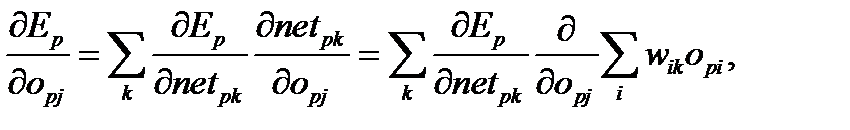 (6.13)
(6.13)
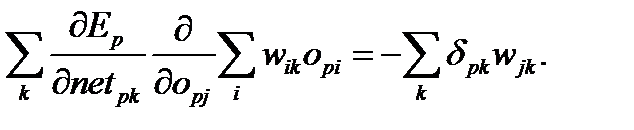 (6.14)
(6.14)
Здесь сумма по 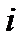 исчезает, поскольку частная производная не равна нулю только лишь в одном случае, также как и в (6.4). Подставив (6.11) в (6.8), получим окончательное выражение:
исчезает, поскольку частная производная не равна нулю только лишь в одном случае, также как и в (6.4). Подставив (6.11) в (6.8), получим окончательное выражение:
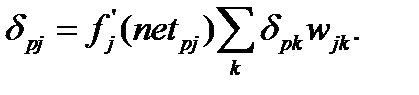 (6.15)
(6.15)
Уравнения (6.12) и (6.15) составляют основу метода обучения многослойной сети.
Преимущество использования сигмоидной функции в качестве нелинейного элемента состоит в том, что очень напоминает шаговую функцию и, таким образом, может демонстрировать поведение, подобное, естественному нейрону [81]. Сигмоидная функция определяется как
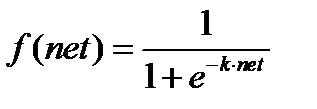 , (6.16)
, (6.16)
и имеет диапазон 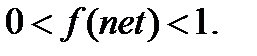
Здесь 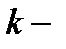 положительная константа, влияющая на растяжение функции: увеличение
положительная константа, влияющая на растяжение функции: увеличение 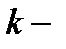 сжимает функцию, а при
сжимает функцию, а при 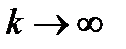 функция
функция 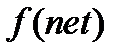 приближается к функции Хевисайда [94]. Этот коэффициент может использоваться в качестве параметра усиления, поскольку для слабых входных сигналов угол наклона будет довольно крутым и функция будет изменяться быстро, производя значительное усиление сигнала. Для больших входных сигналов угол наклона и, соответственно, усиление будут намного меньшими. Это означает, что сеть может принимать большие сигналы и при этом оставаться чувствительной к слабым изменениям сигнала.
приближается к функции Хевисайда [94]. Этот коэффициент может использоваться в качестве параметра усиления, поскольку для слабых входных сигналов угол наклона будет довольно крутым и функция будет изменяться быстро, производя значительное усиление сигнала. Для больших входных сигналов угол наклона и, соответственно, усиление будут намного меньшими. Это означает, что сеть может принимать большие сигналы и при этом оставаться чувствительной к слабым изменениям сигнала.
Однако главный смысл в использовании данной функции состоит в том, что она имеет простую производную, и это значительно облегчает применение backpropagation-метода. Если выход нейрона 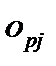 задается как
задается как
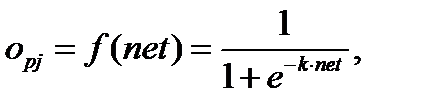 (6.17)
(6.17)
то производная по отношению к данному нейрону 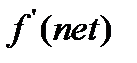 вычисляется так:
вычисляется так:
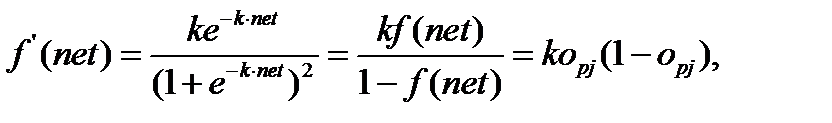 (6.18)
(6.18)
т.е., является простой функцией от выходов нейронов.
