Генетическое программирование

Проблемы компьютерного синтеза программ [86] стали одним из направлений искусственного интеллекта примерно в конце 50-х годов. Попытки автоматической генерации программ, решающих представленную задачу, привели к достаточно скромным результатам, что вполне объяснимо тогдашним состоянием вычислительных систем Hardware и Software. Начиная с середины 80-х годов интерес исследователей к данной проблематике резко возрос, благодаря работам [84, 85] по генетическому программированию, представленных в рамках первой и последующих международных конференций по ГА. Наиболее значительными следует признать работы Дж. Коzа, опубликованных в виде 2-х томов под названием «Генетическое программирование» [84, 85].

Основы ГП.

ГП представляет собой одно из направлений ГА и ориентировано в основном на решение задач автоматического синтеза программ на основе обучающих данных путем индуктивного вывода.

Хромосомы или структуры, которые автоматически генерируются с помощью генетических операторов, являются компьютерными программами различной величины и сложности. Программы состоят из функций, переменных и констант.Исходная популяция P(0) хромосом в ГП образуется стохастически и состоит из программ, которые включают в себя элементы множества проблемно-ориентированных элементарных функций (functionset), а также проблемно-ориентированные переменные и константы (terminalset). Множества functionset и terminalset являются основой для эволюционного синтеза программы, способной наилучшим образом решать поставленную задачу. Одновременно устанавливаются правила выбора элементов из указанных множеств в пространстве всех потенциально синтезируемых программ, структура которых имеет древовидную форму.

Понятно, что множества terminalset и functionset, а также правила их обработки оказывают серьезное влияние на размерность пространства поиска наилучшего решения и на качество результатов, получаемых методами ГП. ГП-структуры как правило имеют древовидную форму.

Koza в своих исследованиях по ГП применяет язык LISP, обладающий всеми необходимыми для синтеза ГП-структур свойствами:

1. LISP (Маккартни Дж.) [93] является синтаксически простым функциональным языком, программа на котором, представляет собой рекурсивную функцию символьных выражений, состоящих из элементарных функций, условных операторов и операторов суперпозиции;

2. Обработка данных в LISP-программе сводится к объединению, делению и перегруппировке информации;

3. LISP-выражения представляются древовидной структурой (рис. 5.1), форма и величина которой может динамически изменяться.

Рис. 5.1. Дерево LISP-выражения (* 11(+314)).

Язык LISP имеет свои недостатки и применение ГП нельзя связывать лишь с LISP-программированием, что нашло свое подтверждение в работах, где для целей ГП применяются языки C, Smalltalk, C++.

Стартовыми, по Koza, условиями для ГП являются:

· установка множества terminal set;

· установкамножества function set;

· определение подходящего вида функции соответствия (fitness-function);

· установка параметров эволюции;

· определение критерия остановки моделирования эволюции и правил декодирования результатов эволюции.

Поскольку основой моделирования эволюции в ГП являются элементы множеств terminalset и functionset, то в этом смысле выбор пользователем языка программирования будет в дальнейшем определять вид получаемых решений. Что касается установки fitness-function, параметров эволюции и критериев остановки процесса моделирования, то они совпадают с аналогичными этапами других типов ЭА.

В качестве элементов functionsets могут фигурировать следующие:

1. арифметические операции ;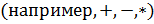

2. математические функции ( );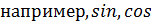

3. булевыоперации (например, if-then- else);

4. циклы (например, for, do-until);

5. некоторые специальные функции, для быстрого поиска хороших решений.

Элементами множества terminalset являются константы и переменные, среди которых особое значение имеют так называемое ephemeralrandom (случайные с коротким временем жизни) константы, в частности для задач связанных с оценкой параметров регрессивных функций.

Koza упоминает о шести различных константах указанного вида. Речь идет о булевых константах, принимающих значения из множества {T, Nil}, а также вещественных константах, принимающих значение на отрезке [-1,000;1,000] с шагом 0,001.

Множества terminalset и functionset должны быть достаточными для нахождения решения задачи, а любая функция быть корректно выполнимой при любых допустимых аргументах (символ операции деления в ГП обозначается через %). Форма fitness-functionимеет большое значение для эффективности ГП.

Общепризнанным способом оценки качества fitness-function является такой показатель, как среднеквадратичная ошибка С.К.О. (чем она меньше, тем лучше программа). Иногда используется критерий «выигрыша», согласно которому выигрыш определяется в зависимости от степени близости к корректному значению целевой функции. Fitness-functionв ГП называют rohfitness и обозначают через

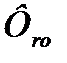. Однако на практике обычно используется стандартное значение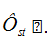

Обозначим через 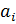некоторую программу из популяции размером 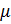. Тогда стандартное значение fitness определяется как

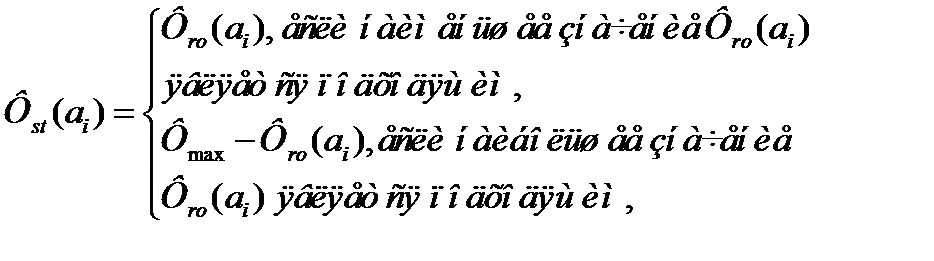(5.2)

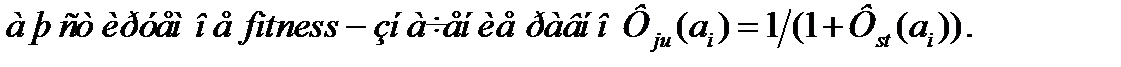
Интервал изменения 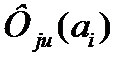равен (0.1). Размер популяции 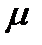в ГП обычно составляет несколько тысяч программ.

Для максимального числа генераций 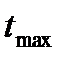рекомендации отсутствуют. Koza в своих экспериментах использует значение 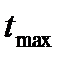=51.

Рассмотрим подробнее процедуру ГП.

1. Инициализация. На этом этапе стохастически генерируется популяция P(0), состоящая из 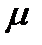древовидных программ, причем корневой вершиной дерева всегда является функция, аргументы которой выбираются случайно из множеств function set или terminal set. Концевыми вершинами дерева должны быть переменные или константы, в противном случае процесс генерации необходимо рекурсивно продолжить. Если структура дерева становится сложной, то заранее устанавливается максимальная высота дерева, равная числу ребер дерева, которое содержит самый длинный путь от корневой вершины до некоторой концевой вершины. В экспериментах Koza максимальная высота дерева колеблется от шести, для популяции P(0), до 17 в более поздних популяциях P(t).

Для обеспечения многообразия популяции P(0) в ходе инициализации Koza предлагает применить так называемый half-ramping способ, согласно которому деревья разной высоты генерируются с одинаковой частотой. Правда этот способ не лишен недостатка, связанного с не совсем случайным характером генерируемых деревьев и в IbaH. предлагаются альтернативные методы «случайной» генерации деревьев начальной популяции P(0), причем дупликация идентичных хромосом в P(0) считается недопустимой.

2. Оценка решений. На 2-м этапе оценивается fitness– функциякаждой программы в P(0), указанным выше способом. Поскольку все программы выбраны случайно, то большинство из них будет иметь fitness– функцию, далекую от лучшего решения, поэтому в качестве оценки можно взять разницу между лучшим и худшим значением fitness– функции в популяции P(0).

3. Генерация новой популяции. Этот этап принято разделять на следующие подэтапы:

a. Выбор операторов эволюции. Основными операторами ГП являются репродукция и кроссинговер, применяемые с вероятностью 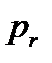и 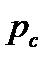соответственно, причем 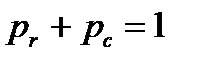(чаще всего ).

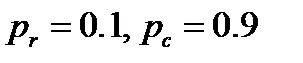b. Селекция и репликация. Данный этап моделирования выполняется по схемам аналогичным ГА.

Образование новой популяции. Если к некоторой программе применяют оператор репродукции, то эта программа копируется в новую популяцию. Для проведения кроссинговера выбираются две родительские хромосомы (программы), случайным образом определяются точки кроссинговера и путем обмена образуются два потомка (рис. 5.2).

Рис. 5.2. Кроссинговер

При программной реализации на языке LISP кроссинговер сводится к обмену списками между двумя программами при сохранении синтаксической корректности вновь получаемых программ.

4. Проверка критерия остановки. Процедура ГП является итерационной, и критерии ее остановки аналогичны критериям для обычных генетических алгоритмов.

В качестве примера, иллюстрирующего рассмотренную процедуру, возьмем следующую проблему:

Проблема двух параллелепипедов

H1

H2

L1

B1 L2

B2

Рис. 5.3. Два параллелепипеда

Пусть два параллелепипеда задаются шестью независимыми переменными L₁, B₁, H₁, L₂, B₂, H₂ и одной зависимой переменной D (рис.5.3.). В таблице 5.2 представлены 10 различных вариантов исходных значений для шести независимых переменных, а также разность объемов D= L_1*B_1*H₁ - L_2*B_2*H₂.

Таблица 5.2

Исходные данные для вычисления разности объемов двух параллелепипедов

	L1	B1	H1	L2	B2	H2	D
							-18
							-171
							-36
							-24
							-155

Пусть до получения корректных значений величины D установлены следующие стартовые условия:

· terminal set T ={ L₁, B₁, H₁, L₂, B₂, H₂};

· function set F ={+, -, *, %};

· rohfitness-функция (функция соответствия) указывает абсолютную ошибку, определяемую разностью между действительным значением D и тем значением, которое получается программно ;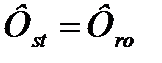

· выигрыш определяется числом случаев, когда сравниваемые величины D различаются менее, чем на 0.01:μ=4000;

· программа останавливается, если число выигрышей равно 10, либо t_max=51.

В результате моделирования эволюции для популяции P(0) лучшая fitness-функция имела значение 783, что соответствовало следующейформе:

(*(―(―B₁L₂)(―B₂H₁))(+(―H₁H₁)(*H₁L₁))) или H₁L₁(B₁+H₁―B₂―L₂).

Видно, что в данном математическом выражении отсутствует переменная H₂ и оно мало похоже на корректное решение. Далее, лучшие fitness-функции в популяциях P(1)-P(6) имели следующие значения: 778, 510, 138, 117, 53, 51. Лучшая программа на восьмом этапе эволюции дала значение fitness, равное 4.44, что соответствовало LISP-выражению следующего вида:

(―(―(*B₁H₁)L₁)(*(*L₂H₂)B₂))(%(+B₁L₁)×(―(―L₁B₂)(+(+B₂L₂)(*L₂B₂)))))

или B₁H₁L₁―B₂H₂L₂―(B₁+L₁)(L₁―2B₂―L₂―L₂B₂).

Видно, что, за исключением последнего ошибочного терма, данное выражение соответствует корректному решению. Наконец, на 11-м шаге эволюции была получена правильная программа вида:

(―(*(*B₁H₁)(L₁)(*(*L₂H₂)B₂)) или L₁B₁H₁―L₂B₂H₂.