Оценки погрешностей измерений и наблюдений за состоянием агрегатов
Точность определения диагностических признаков и последующего оценивания состояния агрегатов зависит от точности измерения исходной информации и особенностей применяемых моделей диагностики (от качества измеряемых параметров и чувствительности к ним моделей). Необходимо отметить также, что уменьшение количества определяемых признаков и оптимизация решения требуемой точности их измерений могут в некоторой степени сократить затраты на процесс измерения как за счет перераспределения требуемой погрешности, так и за счет уменьшения количества измеряемых параметров. Рассмотрим влияние погрешностей измерения на результаты расчета и основанного на них диагноза. Это так называемые прямая и обратная задачи в теории погрешностей [68, 69]. Основу решения обратной задачи составляет нахождение связей между абсолютными погрешностями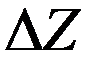 
выходной информации и 
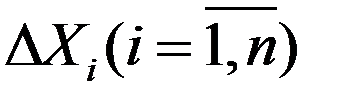- входной информации, чтобы обеспечить заданную (лежащую в заданном интервале доверия) предельную погрешность функции (энергетической характеристики, рис. 3.10) и установить предельные абсолютные погрешности 
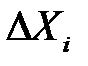ее аргументов. Это так называемый «принцип равных влияний». Суть его заключается в том, что вклад каждого слагаемого в правой части формулы (3.41):
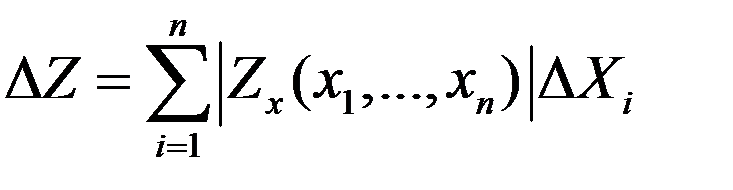, (3.41)
в общую сумму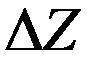 
принят равнозначным. Из этого условия следует равенство
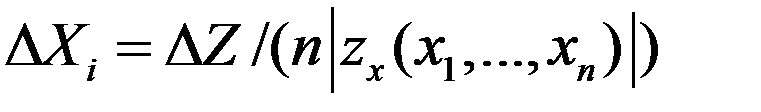, где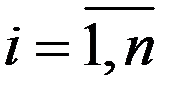 
. (3.42)
Существенным недостатком такого способа является уравнивание различных (с точки зрения физики протекающего в теплоэнергетической установке процесса) параметров погрешностей, формирующих в итоге выходной параметр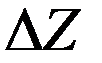 
(мощность, расход и т.д.). В виду этого искажается действительное, статистически проявляющееся соотношение между параметрами, включенными в 
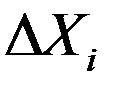(параметрический интервал 
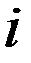- того функционала состояния энергоустановки). Таким образом, появляется нечеткая информация на интервалах нагрузки энергетической характеристики (рис.3.10). В [69] был получен вариант метода наименьших квадратов (МНК), в котором учитываются и погрешности функции и погрешности ее аргументов в приложении к энергоустановке, названный автором «методом согласования балансов». Такой способ анализа данных идентичен «способу согласования балансов», применяемому в энергетике и конфлюэнтному анализу в теории статистики, [70].
Указанный способ не приводит к появлению смещенных оценок идентифицируемых параметров и, в результате, сводится к минимизации суммы
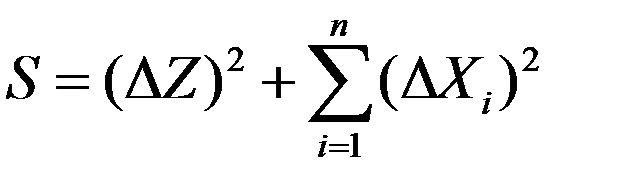, (3.43)
при условии
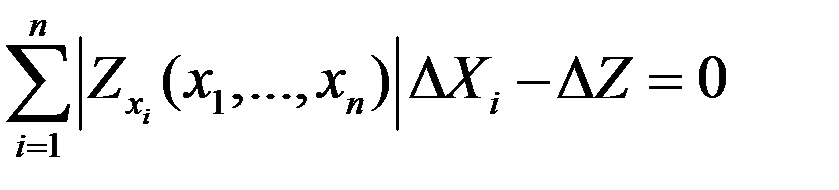. (3.44)
Обратная задача теории погрешностей отвечает условию получения погрешностей независимых аргументов и выполнению условия
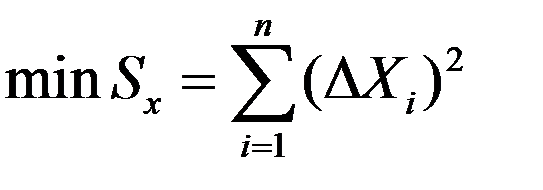, (3.45)
при выполнении условия (3.44) и обязательном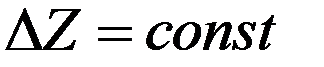 
.
Как показывает выполненный анализ измерений, при диагностических экспериментах на функционирующих энергоустановках, минимизация абсолютных погрешностей не может полностью учитывать имеющееся разнообразие физических и механических параметров (по их абсолютной величине) и, что особенно нежелательно, колебание погрешностей при изменении их аргументов (особенно ощутимое в нестационарных режимах работы энергоустановок и в динамике измерения параметров). В результате это приводит к неопределенности результата измерений – апостериорного состояния системы «объект – средство измерений, процессор».
В связи с изложенным и с учетом [71], в диагностические расчеты и выполняемый анализ результатов измерений признаков вводятся весовые согласующие коэффициенты вида
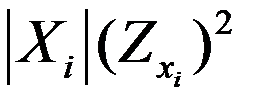. (3.46)
Весовые коэффициенты выбираются диагностом, исходя из условия пропорциональности каждого слагаемого суммы (3.44) абсолютного значения аргумента и квадрата модуля частной производной функции по этой переменной.
Задача минимизации суммы относительных погрешностей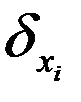 
, в представленной автором постановке, решается в виде
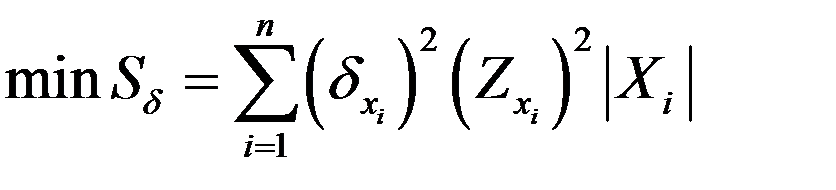, (3.47)
при соблюдении условия (3.44). Для решения этой задачи используется метод множителей Лагранжа Ж.-Л. и программный модуль OPTIMIZATOR (рис. 3.9) диагностического комплекса SKAIS [9], позволяющие отыскивать максимум (минимум) функции при ограничениях в форме равенств. Основная идея применяемого метода заключается в переходе от задачи на условный экстремум к задаче отыскания безусловного экстремума некоторой специально построенной функции Лагранжа Ж.-Л..