Перечень базовых операций над множествами
1. Дополнение А. Если X={x1, x2, x3} и A={x1, x2}, то А={x3};
2. Разность А\В. Если A={x1, x2} и B={x2, x3}, то А\В = {x1};
3. Пересечение (произведение) 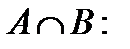 если
если 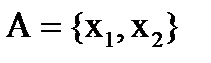 и
и 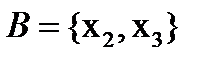 , то
, то 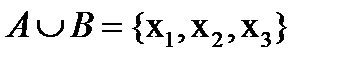 ;
;
4. Объединение (сумма) 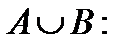 если
если 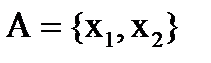 и
и 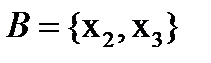 , то
, то 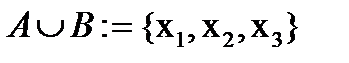 .
.
На универсальном множестве X= { 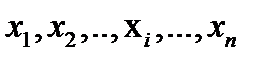 } любое множество А можно записать так:
} любое множество А можно записать так:
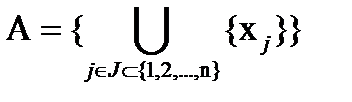 , (1.3)
, (1.3)
где 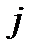 принимает все значения из подмножества
принимает все значения из подмножества 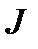 множества натуральных чисел
множества натуральных чисел 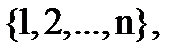 или
или 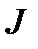 - множество номеров элементов
- множество номеров элементов 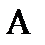 .
.
Например: X = { 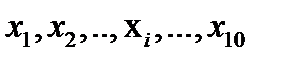 }, при i от 1 до 10 и А = {x1, x4, x6}, можно записать:
}, при i от 1 до 10 и А = {x1, x4, x6}, можно записать: 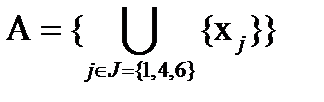 , где
, где 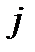 принимает значения 1, 4, 6.
принимает значения 1, 4, 6.
Пусть задано универсальное множество, а в нем определено некоторое пространство, в котором имеется класс множеств.
Аксиома 3: класс множества пространства называется аддитивным, если:
a) всё пространство принадлежит классу;
b) все последовательности вложенных множеств из этого класса, их сумма и произведение принадлежат классу;
c) для множества и его подмножества из этого класса, и их разность - принадлежат классу.
Таким ообразом, признак аддитивности класса: счетное число операций сложения, умножения и вычитания над элементами этого класса, дают результат в том же классе. Например, если пространство равно {x1,x2}, то класс всех его возможных подмножеств есть множество подмножеств {{x1}, {x2}, {x1,x2}} или степенное множество в данном пространстве.
Проверим аддитивность этого класса. В соответствии с аксиомой 3, проверяем условия:
a) в классе множества {{x1}, {x2}, {x1, x2}} имеется элемент {x1, x2} равный пространству {x1,x2}, поэтому оно принадлежит классу {{x1}, {x2}, {x1, x2}};
б) в классе {{x1}, {x2}, {x1, x2}} имеются две последовательности вложенных множеств: {x1} 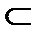 {x1, x2}, {x2}
{x1, x2}, {x2} 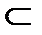 {x1, x2}, в каждой из них сумма и произведение множеств дают результат в том же классе;
{x1, x2}, в каждой из них сумма и произведение множеств дают результат в том же классе;
в) в классе {{x1}, {x2}, {x1, x2}} имеются пары: множество и его подмножество из того же класса -{x1, x2} 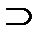 {x1}, {x1, x2}
{x1}, {x1, x2} 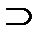 {x2}; в каждой паре разность множества и подмножества дают результат в том же классе.
{x2}; в каждой паре разность множества и подмножества дают результат в том же классе.
Таким образом, условия а), б) и в) справедливы и класс {{x1}, {x2}, {x1, x2}} является аддитивным.
На множестве действительных чисел R определим интервалы как подмножество 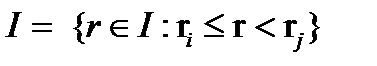 , где ri и rj – точная и неточная границы интервала соответственно:
, где ri и rj – точная и неточная границы интервала соответственно:
ri 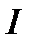 rj R
rj R
Класс всех интервалов 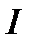 на множестве
на множестве 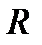 не является аддитивным, т.к. для вложенной последовательности множеств, либо множества и его подмножества, результат суммы, либо разности, не будут принадлежать исходному классу (не выполняется условие б) или в) аксиомы 3.
не является аддитивным, т.к. для вложенной последовательности множеств, либо множества и его подмножества, результат суммы, либо разности, не будут принадлежать исходному классу (не выполняется условие б) или в) аксиомы 3.
Например, класс I1, I2, I3 является аддитивным, так как его элементы не образуют вложенной последовательности R множеств, сумма которых даст результат в том же классе { 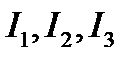 }:
}:
I1 I2 I3 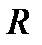
не является аддитивным, так как его элементы не образуют вложенной последовательности множеств, сумма которых даст результат в том же классе 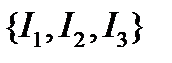 .
.
Выполним процедуру расширения класса интервалов путём счётного повторения операций сложения, вычитания и умножения над элементами класса до тех пор, пока расширенный класс не будет удовлетворять условиям аддитивности, в соответствии с аксиомой 3. Тогда вся совокупность, полученных при расширении множеств, называется классом борелевских множеств [18]. Такой класс ещё называется борелевским полем множеств, множествами, измеримыми по Борелю или минимальной 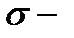 алгеброй множеств. Будем обозначать этот класс
алгеброй множеств. Будем обозначать этот класс 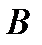 .
.
Рассмотрим, на примере, получение борелевского класса. Пусть на множестве R задан исходный класс интервалов { 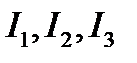 }:
}:
I1 I2 I3 R
Выполним процедуру расширения класса { 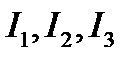 } в класс {R1, R2, R3, R4, R5, R6, R7} следующим образом:
} в класс {R1, R2, R3, R4, R5, R6, R7} следующим образом:
R1 = I1 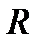
R2 = I2 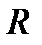
R3 = I3 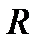
R4 = 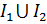
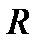
R5 = 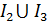
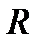
R6 = 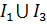
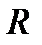
R7 = 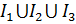
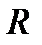
Теперь проверим аддитивность полученного класса.
По аксиоме 3 условия аддитивности следующие:
а) в классе {R1÷R7} элементы R1, R2 и R3 равны элементам пространства I1, I2, I3 соответственно. Поэтому всё пространство 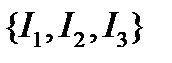 принадлежит классу {R1
принадлежит классу {R1  R7};
R7};
в) в классе {R1÷R7} имеются шесть последовательностей вложенных множеств, каждое из которых сумма и произведение множеств дают результат в том же классе:
R1  R6
R6  R7; R3
R7; R3 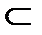 R6
R6 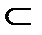 R7;
R7;
R1 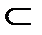 R4
R4 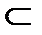 R7; R2
R7; R2 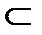 R4
R4 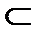 R7;
R7;
R3 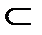 R5
R5 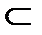 R7; R2
R7; R2 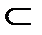 R5
R5 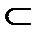 R7.
R7.
Например, R1  R6 = R6.
R6 = R6.
с) в классе {R1÷R7} имеются пары: множество и его подмножество из того же класса, в каждой паре разность между множеством и подмножеством дает результат в том же классе: R4 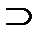 R1; R4
R1; R4 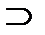 R2; R5
R2; R5 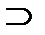 R2; R5
R2; R5 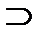 R3; R6
R3; R6 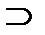 R3; R7
R3; R7 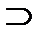 R6; R7
R6; R7 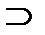 R4; R7
R4; R7 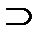 R5; R7
R5; R7 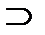 R1; R7
R1; R7 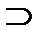 R2; R7
R2; R7 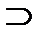 R3. Например, R4 \ R1 = R2.
R3. Например, R4 \ R1 = R2.
Таким образом, условия аддитивности выполняются и полученный класс – борелевский: В = {R1÷R7}.
1.4. Области определения функций
Условиям аддитивности удовлетворяют степенное множество 2А в некотором пространстве А и борелевский класс В, в пространстве интервалов множества действительных чисел R. Поэтому в теории нечетких множеств существуют дискретная и непрерывная области определения: 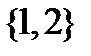 .
.
1) Дискретная область определения.
Пусть задано универсальное множество X:
X={x1,x2,..,xi,…,xn}, i=1÷n. (1.4)
В Х определено пространство А:
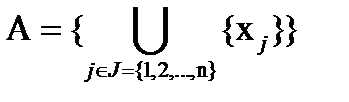 . (1.5)
. (1.5)
На множестве J номеров элементов пространства А образовано множество К=2J, т.е. степенное множество. Тем самым, в А построен аддитивный класс 2А:
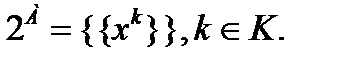 (1.6)
(1.6)
Этот класс является дискретной областью определения различных функций в теории нечётких множеств. В частном случае, если А=X, областью определения является 2X.
2) Непрерывная область определения. Пусть задано универсальное множество R, элементы которого принадлежат множеству r. На R определено пространство интервалов А:
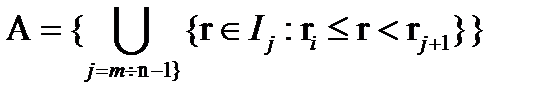 , (1.7)
, (1.7)
где Ij - интервал с границами rj и rj+1; m, n – границы пространственных интервалов А.
В А построен борелевский класс В:
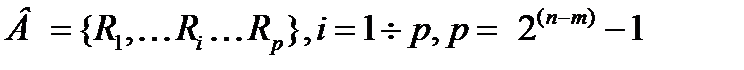 , (1.8)
, (1.8)
где 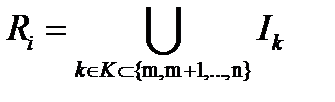 .
.
Класс В является непрерывной областью определения различных функций в теории нечётких множеств.
3)
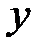
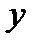 |
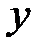 |
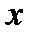 |
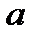 |
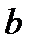 |
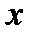 |
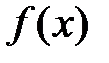
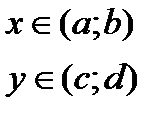
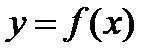 - числовая функция от х.
- числовая функция от х.
Если каждому значению х из (a; b) по какому- нибудь закону или правилу f
поставлено в соответствие одно определенное значение другой величины
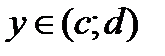 , то говорят, что
, то говорят, что 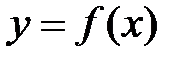 – есть числовая функция от х.
– есть числовая функция от х.
х – аргумент;
(a, b) – область определения функции;
(c,d) – область значений функций.
Например: y = sinx; y = x²;
х – независимая переменная,
 |
 |
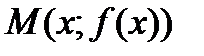 |
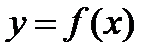 |
 } } |
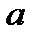 |
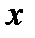 |
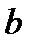 |
Множество точек М (х; у), где 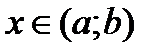 ,
, 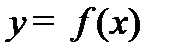 называется графиком функции
называется графиком функции 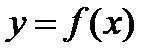 .
.
Простейший вид заданного типа функции называется базовой функцией.
Пример, 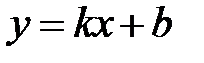 - линейная функция. Базовой функцией будет являться функция
- линейная функция. Базовой функцией будет являться функция 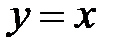 .
.
При построении функции заданного типа предварительно строим график базовой функции.
Пример: Построить график функции 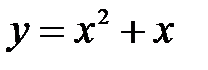 .
.
Перед нами – квадратичная функция. Ее графиком является парабола. Базовой функцией будет являться функция 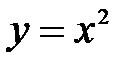 .
.
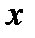 |
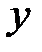 |
Для построения нашей функции выделим полный квадрат:
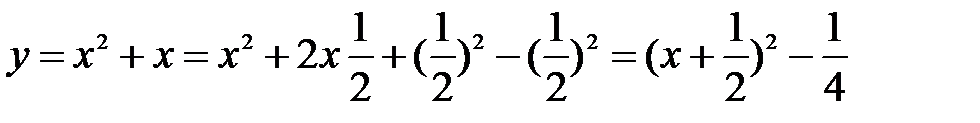
График нашей функции строится в три этапа:
1. Строим график базовой функции 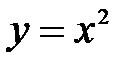
2. Сдвигаем нашу функцию на 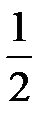 влево:
влево: 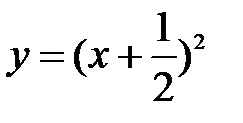
3.
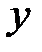 |
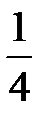 вниз.
вниз.
График функции 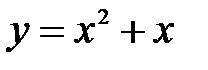 |
 |
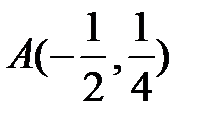 |
Понятие сложной функции
Для освоения понятия сложной функции введем в рассмотрение промежуточную числовую ось z.
Для примера рассмотрим функцию 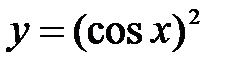 . Для этой функции, для заданного х, предварительно вычисляется
. Для этой функции, для заданного х, предварительно вычисляется 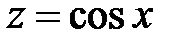 . Для полученного значения z вычисляется
. Для полученного значения z вычисляется 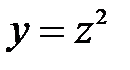 . Таким образом, в два приема, для заданного х, мы получили значение
. Таким образом, в два приема, для заданного х, мы получили значение 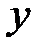 . Такое задание
. Такое задание 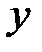 от х называется сложной функцией.
от х называется сложной функцией.
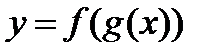 – сложная функция от х. – сложная функция от х. |
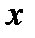 |
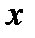 |
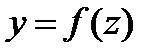 |
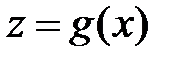 |
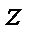 |
Промежуточных числовых осей может быть несколько.
Например:
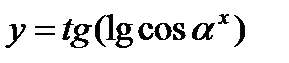
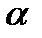 |
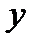 |
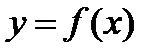 |
 |
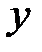 |

 |
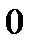 |
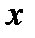 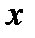 |
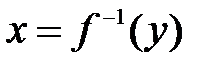 |
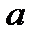
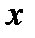
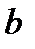
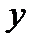 |
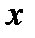 |
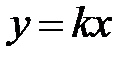 |
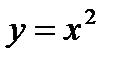 |
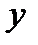 |
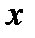 |
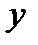 |
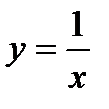 |
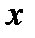 |
Элементарной функцией будем называть базовую функцию или функцию,
полученную путем четырех арифметических действий из базовых функций, или
взятия сложной функции, последовательно применяемых конечное число раз
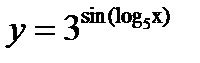 .
.
Говорят, что функция 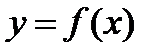 непрерывна в точке
непрерывна в точке 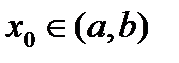 ,если выполнены следующие условия:
,если выполнены следующие условия:
1. 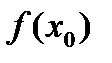 – существует значение функции в точке
– существует значение функции в точке 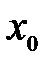
2. существуют пределы функции слева и справа при 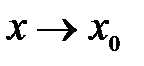
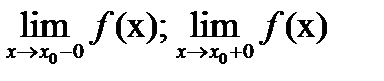
3. все полученные нами числа должны быть равны между собой.
И записывается это так:
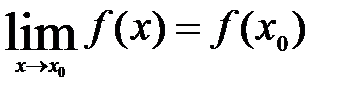
Так как, 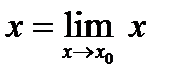 ,то условие непрерывности примет вид
,то условие непрерывности примет вид
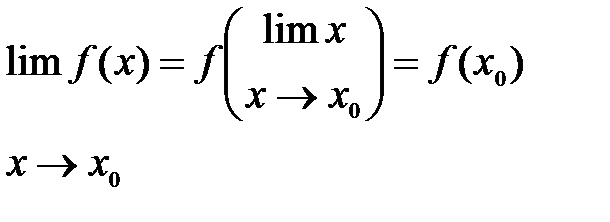
 |
 |
Для непрерывной функции знак предела и знак функции можно переставлять местами.
Разрывная функция
| Конечный скачок |
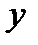 |
| } |
| скачок |
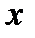 |
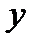 |
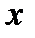 |
| Бесконечный скачок |
Устранимый скачок: предел слева равен пределу справа, а в точке 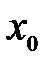 значение значение 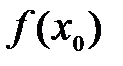 не существует, или не совпадает с пределами. не существует, или не совпадает с пределами. 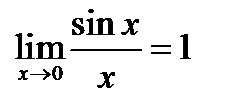 |
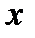 |
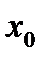 |
В точке 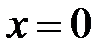 значение функции вычислить нельзя, так как на 0 делить нельзя.
значение функции вычислить нельзя, так как на 0 делить нельзя.
Теорема
Всякая элементарная функция непрерывна в области своего определения:

Мера и нечеткая мера
Понятие меры было введено для частных случаев Э. Борелем [18], К. Жорданом [19] и А. Лебегом [20]. В современной теории меры Banon G. формулирует его следующим образом, [11].
Пусть заданы области определения: аддитивный класс 2x в пространстве X на универсальном множестве X; значения – множество действительных чисел R. Функция множества называется мерой  , если выполняются условия {1,2,3}:
, если выполняются условия {1,2,3}:
1) ограниченность -  ;
;
2) неотрицательность -  ;
;
3) аддитивность -  .
.
В теории нечётких множеств используется понятие «нечеткая мера», на основе которой определяется функция доверия.
Пусть теперь заданы области определения, аддитивный класс 2А в пространстве А на универсальном множестве X; значения - отрезок [0,1] на множестве действительных чисел.
Функция множества называется нечеткой мерой g:
 , если выполняются условия {1,2,3}:
, если выполняются условия {1,2,3}:
1) ограниченность – g (Ø) = 0, g(x)=1;
2) монотонность – для 
3) непрерывность – для An  2A и монотонной последовательности
2A и монотонной последовательности 
Тройка  называется пространством с нечеткой мерой.
называется пространством с нечеткой мерой.
