Переработка и использование информации в реальных условиях

КРОХИН Г.Д.

ИНТЕЛЛЕКТУАЛЬНЫЕ ТЕХНОЛОГИИ

В ЗАДАЧАХ УПРАВЛЕНИЯ

Учебное пособие

Новосибирск

АННОТАЦИЯ

В учебном пособии представлены теоретические и практические интеллектуальные технологии, для использования в задачах управления технологическими и информационными процессами экономических промышленно-хозяйственных производств, включая теплоэнергетику-производителя тепла и электроэнергии для народного хозяйства, строительства зданий и сооружений для населения городов России.

При этом особое внимание уделяется теоретическим и практическим технологиям для повышения уровня эффективности, экономичности, экологической безопасности и надежности работы оборудования, бесперебойного энергоснабжения, безопасного жизнеобеспечения, снижения вероятности и предупреждения возникновения аварийных ситуаций и другим вопросам, в частности, диагностике, мониторингу учета состояния оборудования и информационным вопросам обеспечения промышленности и урбанистики городов-гигантов.

Автор ориентируется на аппаратно, программно и экспериментально полученные и апробированные алгоритмы обработки четкой и нечеткой информации.

В учебном пособии рассмотрены и предложены научно-технические решения, алгоритмы и математические модели для моделирования в исследовании сложных плохо формализуемых технологических процессов гибридных систем с применением нечеткой логики и нечетких множеств, которые ранее не применялись в промышленном производстве, энергетике и народном хозяйстве.

Предисловие

В настоящее время все большее значение приобретают разработки в области информатики – аппаратно, программно и процессорно - реализованные интеллектуальные алгоритмы обработки информации для применения их к различным технологиям интеллектуального управления. Это оказалось связанным с прогрессом применения мониторинга в экономических и в технических системах. Но эти методы получались малоэффективными. Особенно широкое применение в технической диагностике получил аппарат нечетких систем: нечеткая логика, нечеткие множества, нейронные сети, генетические алгоритмы, ассоциативная память, экспертные системы и ряд других интеллектуальных и гибридных информационных технологий, которые не применялись ранее в промышленности, строительстве, народном хозяйстве и в энергетике России.

Уже сегодня задачи, решаемые такими интеллектуальными технологиями информационных систем, в большинстве случаев, можно свести к ряду основных, т.е. государственной важности, среди которых выделяются следующие:

1) безаварийное, бесперебойное и эффективное энерго-использование, экологически чистое при производстве товаров народного потребления и жизнеобеспечения населения страны;

2) увеличение сроков службы и повышение уровня надежности работы основного и вспомогательного оборудования промышленного и энергетического производства;

3) повышение уровня безопасности работы в промышленных установках за счет возможности контроля состояния действующих агрегатов с помощью интуитивно – понятийного интерфейса АРМ-ов оперативно – эксплуатационного персонала, а также отдельных АРМ-ов систем и подсистем, входящих в АСУТП и АСУ технологического производства, народного и жилищно-коммунального хозяйства, использования блокировок коммутационных аппаратов и т.д.;

4) повышение уровня экономической эффективности и безопасности эксплуатации (и технического обслуживания) основного и вспомогательного оборудования энергетических агрегатов промышленного производства по его состоянию;

5) повышение качества управленческих и организационных решений в части управления жизненным циклом промышленных предприятий и жилищно-коммунального хозяйства, строительстве зданий и сооружений для поышения урбанизма населения и городов России.

В данном учебном пособии представлена возможность расширить применение аппарата и методов нечетких и гибридных систем и, соответственно, углубить методологию технической диагностики в приложении к техногиям анализа состояния сложных технических систем, особенно в условиях обработки неопределенных данных.

Материал в учебном пособии представлен таким образом, чтобы он соответствовал всем стадиям создания информационных интеллектуальных систем, гибридных технологий в информационных системах и системах искусственного интеллекта.

Материалы учебного пособия частично использовались в течение нескольких последних лет при обучении студентов старших курсов НГУЭУ, магистрантов, аспирантов и слушателей курсов повышения квалификации специалистов-энергетиков при чтении автором следующих учебных курсов: «Системный анализ в энергетике», «Системы искусственного интеллекта», «Информационные интеллектуальные системы в энергетике», «Живучесть ТЭС», «АСУ ТЭС», «Системная инженерия», «Нечеткие технологии», «Интеллектуальные системы и технологии», «Гибридные технологии в информационных системах» и «Специальные главы математики» на факультетах энергетики и АВТФ НГТУ, ПЭИ п.к. (г. Новосибирск), информационно-техническом факультете НГУЭУ (г. Новосибирск), академии архитектуры АРХИ (г. Новосибирск) и АСУ ТЭС ИТУ МЭИ (г. Москва).

ВВЕДЕНИЕ: А, Б

А. Основные понятия, термины и определения современной математики, используемые в интеллектуальных технологиях информационных систем

Б.Элементы теории множеств, операции над множествами, кванторы

Часть 1.

Глава 1. Математические основы формализации и методов описания интеллектуальных технологий информационных систем в задачах управления

1.1. Представления композиции отношений матрицами и графами

1.2. Формализация объекта и парадигмы

1.3. Множества и перечень базовых операций над множествами

1.4. Области определения функций

1.5. Мера и нечеткая мера

1.6.Нечеткие множества: определение и формы записи в операциях и методах представления знаний

1.7.Функции доверия и правило Демпстера

1.8. Нормировка функций в теории нечётких множеств

1.9. Нечёткие отношения: прямая и обратная задачи

Часть 2.

Глава 2. Методы представления знаний с использованием

приближенных множеств

2.1. Интеллектуальные вычислительные технологии

2.2. Семантика объекта: определение и типизация

2.3. Создание Базы знаний: постановка, семантика, прагматика

2.4. Сопоставление объектов: постановка, семантика, прагматика

2.5. Распознавание объектов: постановка, семантика, прагматика

2.6. Управление процессом представления знаний

2.7. Нечёткие множества: субъективность и неточность

2.8. Нечеткая алгебра

2.9. Нечеткие иерархические отношения

2.10. Естественность операций max и min

2.11. Нечеткая статистика

2.12. Совместимость и нечеткое ожидание

Контрольные вопросы и задания для самостоятельной работы по главам 1 и 2.

Часть 3.

Глава 3. Интеллектуальные технологии создания информационных систем. Способы получения информации и ее реализации для оценивания состояния агрегатов систем

3.1. Формализация диагностического эксперимента и требования к измерениям

3.2. Обработка нечетких данных как неопределенных чисел

3.2.1. Методология представления агрегата в виде комплексного механизма

3.2.2. Описание исходной информации на языке размытых множеств

3.3. Выбор состава множеств распознающих параметров

3.3.1. Методы группирования данных, классификации и кластеров

3.3.2. Размытость интервалов, ограничений, критериев и целей управления

в эксплуатации и диагностике

3.3.3. Размытые ограничения, цели и оптимизация работы механизма в условиях нечеткой информации о состоянии

3.3.4. Распознавание образов и сходства

3.4. Анализ информации для диагностики и оценивания состояния механизмов

3.5. Оценки погрешностей измерений и наблюдений за состоянием агрегатов

3.6. Влияние погрешностей исходных данных на погрешности диагноза

Контрольные вопросы и задания для самостоятельной работы по главе 3.

Часть 4.

Глава 4. Источники информации и причины возникновения ее неопределенности

Функционирования агрегатов

4.2. Управление и идентификация объектов в условиях неопределенности

информации на основе знаний, получаемых при функциональной диагностике

4.3. Представление и использование четких и размытых знаний в математических моделях оценивания состояния на основе функциональной диагностики

4.3.1. Формализация решения задачи оценивания состояния

4.3.2. Особенности решения задач контроля и функционирования агрегата

Контрольные вопросы и задания для самостоятельной работы по главе 4.

Часть 5.

Глава 5. Введение в генетическое программирование

5.1. Введение в генетические и эволюционные алгоритмы

5.2. Сравительный анализ эволюционных алгоритмов

5.3. Генетическое программирование

5.4. Перспективные направления развития генетического программирования

Контрольные вопросы и задания для самостоятельной работы по главе 5.

Часть 6.

Глава 6. Введение в нейронные сети

6.1. Алгоритмы их обучение и эластичные нейро-нечеткие системы

6.2. Имитация нервных клеток

6.3. Математическая модель нейрона

6.4. Обучение нейронных сетей

6.5. Метод обратного распространения ошибки

6.6. Алгоритм настройки нейронной сети

Контрольные вопросы и задания для самостоятельной работы по главе 6.

Часть 7.

Глава 7. Другие методы интеллектуальных технологий в задачах управления

7.1. Введение в теорию возможностей и смысла

7.1.1. Неопределенность и неточность

7.1.2. Традиционные модели неточности и неопределенности

7.1.3. Меры неопределенности

7.1.4. Меры возможности и необходимости

7.1.5. Возможность и вероятность

7.2. Языки и технологии логического программирования PROLOG, LISP

Контрольные вопросы и задания для самостоятельной работы по главе 7.

Часть 8.

Глава 8. Послесловие

8.1. Эволюция ИИ для развития интеллектуальных технологий информационных систем

8.2. Экспертные системы нового уровня

8.3. Роботика

8.4. Преобразование речи искусственного языка

8.5. Интеллект муравьев и его использование

8.6. Искусственная жизнь, мозг, познание, разум, память и мышление

8.7. Боты

8.8. Нечеткая оптимиация в задачах теплоэнергетики и промышленности

8.9. Применение искусственного интеллекта в архитектонике урбанизированного пространства

Контрольные вопросы и задания для самостоятельной работы по главе 8.

ЗАКЛЮЧЕНИЕ

СПИСОК ЛИТЕРАТУРЫ

Гл. 4. Посвящена рассмотрению решений конкретных задач – источники информации и причины возникновения ее неопределенности, применение теории нечетких множеств и нечетких логик при разработке моделей диагностики и оценивании состояния агрегатов. Предложены критерии адекватности полученных нечетких моделей.

Гл. 5 и 6. Введение в генетическое программирование и нейронные сети. Таким образом, в учебном пособии изложены основные направления развития и результаты практики применения современных информационных технологий в задачах управления энергетики и промышленности.

Гл. 7 и 8. Представлены другие методы нечетких технологий (включая и когнитивных нейронаук), необходимые для построения информационных интеллектуальных систем.

В послесловии кратко изложены новые методы и эволюции применения ИИ для развития интеллектуальных технологий информационных систем с развернутым примером применения методологии ИИ в урбанизме населения и городов.

На протяжении всей книги материал излагался, по возможности, с единых позиций при сохранении приемлемого уровня строгости. Всюду, где это оказалось возможным, привлекались математические средства, именно в качестве средств, а не предмета изложения.

Учебное пособие может быть использовано студентами старших курсов, магистрантами, аспирантами и специалистами в области прикладной математики, информатики и интеллектуальных информационных технологий.

А. Основные понятия, термины и определения современной математики, используемые в интеллектуальных технологиях информационных систем

Множество, кортеж, соответствие, функция, отношение:

Множество S – есть любое собрание определённых и различных между собой объектов нашей интуиции (или интеллекта) мнимое, как единое целое. Эти элементы или объекты называются элементами или членами множества S: .

Теория множеств создана Георгом Кантором (1845 – 1918). Проводившиеся Кантором исследования, которые относились к тригонометрическим рядам и числовым последовательностям, привели его к задаче вычисления тех средств, которые необходимы для сравнения бесконечных множеств чисел по величине.

Для решения проблемы Г. Кантор [1] ввёл понятие мощности множества. Считают, по определению, что два множества имеют одинаковую мощность, если члены любого из них можно сопоставить членам другого, образовав пары соответствующих членов, поскольку между членами двух конечных множеств можно установить такое парное соответствие в том случае, когда они имеют одинаковое число членов.

Мощность можно отождествить с конечным числом. Таким образом, понятие мощности бесконечного множества представляет собой обобщение обычного понятия количественного числа. Кантор построил теорию таких обобщённых (трансфинитных) чисел, включающих в себя их похожесть.

Кортеж– упорядоченный набор конечной последовательности, представляющий из себя вектор, то есть составной объект, имеющий определённое число компонентов или составляющих. Составные векторы стоят на соответствующих местах и обозначаются: <a₁, a₂, …, a_n>. Кортеж с несовпадающими элементами представляет собой размещение.

Соответствие – предполагает наличие двух множеств: области отправления и области прибытия. Областью отправления могут быть множества весов, людей, цветов, существительных, слов языка. Областью прибытия будет множество весов, ростов, цветов, людей, окончаний.

Функция - это:

1. Зависимость;

2. Переменная величина, значения которой изменяются в зависимости от условий значения другой величины [2];

3. Закон (правило), по которому значения независимых переменных отвечает (соответствует) значениям рассмотренной зависимой переменной [3];

4. Если поставим в соответствие множеству X, состоящему из элементов x, множество Y, состоящее из элементов y, то можно сказать, что имеется отображение множества X на множестве Y, то есть функция f, аргументы которой находятся во множестве X, а значение - во множестве Y [4].

Пусть X – некоторое множество на числовой прямой. Говорят, что на этом множестве определена функция f, если каждому числу , поставлено в соответствие число , то есть, y = f(x). X – область определения данной функции, Y – область значений.

Н.Н. Лузин [5] трактует, что функция – это соответствие, в силу которого, каждому элементу , отвечает единственный элемент .

Никола Бурбаки [6] утверждает: функция – это, когда каждому элементу области отправления соответствует элемент области прибытия.

Пример:

a) y = x², ,

b) y = , и .

Отношение – это пара, состоящая из двух множеств, причём элементы первого из множеств служат парой элементам второго множества.

Композиция отношений (связь). Пусть даны множества X, Y, Z и два отношения: , .

Композиция отношений A и B есть отношение C из всех тех пар для которых , .

Сечение отношения C по X совпадает с сечением отношения B, включает , , C = AB .

Такая запись имеет следующие преимущества. Композиция отношений обладает ассоциативным законом, то есть D(BA) = DB(A) = DBA, но не коммутативна, то есть . Так же (BA)^-1 = A^-1*B^-1.

Часть 1.

Теорема

Всякая элементарная функция непрерывна в области своего определения:

Мера и нечеткая мера

Понятие меры было введено для частных случаев Э. Борелем [18], К. Жорданом [19] и А. Лебегом [20]. В современной теории меры Banon G. формулирует его следующим образом, [11].

Пусть заданы области определения: аддитивный класс 2^x в пространстве X на универсальном множестве X; значения – множество действительных чисел R. Функция множества называется мерой , если выполняются условия {1,2,3}:

1) ограниченность - ;

2) неотрицательность - ;

3) аддитивность - .

В теории нечётких множеств используется понятие «нечеткая мера», на основе которой определяется функция доверия.

Пусть теперь заданы области определения, аддитивный класс 2^А в пространстве А на универсальном множестве X; значения - отрезок [0,1] на множестве действительных чисел.

Функция множества называется нечеткой мерой g:

, если выполняются условия {1,2,3}:

1) ограниченность – g (Ø) = 0, g(x)=1;

2) монотонность – для

3) непрерывность – для A_n 2^A и монотонной последовательности

Тройка называется пространством с нечеткой мерой.

Нечеткая алгебра

Определение 1: Нечеткой алгеброй называется система:

Z = <Z,+,*, > , где Z – множество, имеющее хотя бы 2 различных элемента и система Z удовлетворяет следующему набору аксиом:

1. идемпотентность: ;

2. коммутативность: ;

3. ассоциативность: ;

4. поглощение: ;

5. дистрибутивность:

6. дополнение: если то существует дополнение элемента х такое, что ;

7. единичные элементы: такой, что

8. закон Де Моргана, [39]: , (2.20)

Эта система, из 8 аксиом, образует дистрибутивную структуру с единственными единичными элементами относительно операций суммирования (+) и умножения( ). К сведению, булева алгебра [40] так же является дистрибутивной структурой с дополнениями и с единственными единичными элементами, относительно этих же операций. Однако для любого элемента х в булевой алгебре справедливы равенства:

. (2.21)

Данные соотношения для нечеткой алгебры, вообще говоря, не верны. Таким образом, любая булева алгебра является нечеткой, но не наоборот.

В данном изложении мы будем пользоваться конкретной нечеткой алгеброй, которая определяется системой: Z = <[0,1],+,*, > , где в качестве операций сложения и умножения служат соответственно операция взятия максимума и минимума, а дополнение определяется как

.

Единственными единичными элементами служат соответственно 0 и 1, которые при любых x удовлетворяют равенствам:

.

Пусть, как и ранее, Ω = {x} – пространство объектов, а А и В – два нечетких множества в Ω.

В близком соответствии с терминологией Заде, введем следующие понятия:

Равенство А=В определим как А=В .

Нечеткое множество А содержится в множестве В*(А ), тогда и только тогда, когда

Нечеткое множество является дополнением нечеткого множества А, тогда и только тогда, когда

Объединением двух нечетких множеств А и В из Ω назовем множество А+В с функцией принадлежности .

Пересечением двух множеств А и В из Ω назовем множество А В с функцией принадлежности .

Далее, вместо термина,«степень принадлежности переменной к множеству», будем употреблять - термин «нечеткая переменная». Условимся так же опускать символ , то есть, вместо , будем писать x y.

Совершенно очевидно, что, среди бесконечного числа разных способов присвоения переменным степени принадлежности конечному множеству, существует лишь конечное число двоичных способов (то есть, присвоения всем переменным значения 0 и 1). Л. Заде определяет нечеткое отношение R как нечеткое множество упорядоченных пар. Таким образом, если совокупности объектов x и y, то нечеткое отношение из X в Y – это нечеткое подмножество прямого произведения , характеризуемое функцией принадлежности (характеристической функцией) которая каждой паре (x, y) ставит в соответствие «степень принадлежности» к R. Для простоты предположим, что областью значения функции служит отрезок [0,1], а число будем называть силой отношения между x и y.

Областью определения, (domain, domR) нечеткого отношения R, назовем НМ с функцией принадлежности

. (2.22)

Аналогично, областью значений (range, ranR) отношения R, назовем нечеткое множество с функцией принадлежности

. (2.23)

Высотой h(R) – называется число h(R):

(2.24)

Нечеткое отношение называется нормальным, если h(R)=1, и субнормальным, если h(R)<1.

Носителем S(R) отношения R назовем четкое подмножество прямого произведения X×Y, на котором .

Замечание 1: если X и Y – конечные множества, то функцию можно представить в виде матрицы, (x,y) –й элемент которой равен

Нечеткая статистика

Мотивировка - обычно неточность и неопределенность рассматривают, как случайные статистические характеристики и учитывают их с помощью методов теории вероятностей. В реальных ситуациях неточность, часто обусловлена не только наличием случайных переменных, но и принципиальной невозможностью работать с точными данными (их просто нет, или очень мало), из-за сложности системы или неточности ограничений и цели. Это возникло в связи с необходимостью решения труднорешаемых проблем и задач. Сегодня в реальных задачах стали обращать внимания на классы объектов с нечетко определенными границами. В связи с появлением теории Заде, неточность стали выражать таким образом, что объект может либо принадлежать, либо не принадлежать какому-то определенному классу, или же иметь к нему некоторую промежуточную степень принадлежности. Отрезок [0,1] позволил ученым решать задачи именно в этом интервале, то, что раньше мы не могли себе позволить.

Интуитивно понятия неточности и вероятности кажутся сходными. Это сходство подчеркивается и подтверждается тем обстоятельством, что интервал, изменяющий степени принадлежности к нечетким множествам, совпадает с отрезком [0….1]. Однако, между понятиями «нечеткость» и «вероятность» имеются существенные отличия, вероятность – объективная характеристика и выводы теории вероятностей могут быть экспериментально обоснованы, с другой стороны степень принадлежности является субъективной характеристикой. Т.е., маловероятно, с позиции теории вероятностей, чтобы событие имело малую вероятность, точнее, имело малую степень принадлежности. На самом деле тщательный анализ нечетких переменных показывает, что их можно разбить на два класса: статистический и не статистический. Отличие теории нечетких множеств состоит также и в том, что в ней, в отличие от теории вероятностей, в качестве основных операций, используются операции нахождения минимумов и максимумов, поэтому возможным обоснованием эффективности методов теории нечетких множеств может послужить решение на основе этой теории достаточно большего числа практических задач. Как известно, теорию вероятностей, как систематическую науку, можно построить на базе 3-х аксиом, совпадающих с соответствующими аксиомами теории меры. Необходимость развития нечеткой статистики обусловлена её методологической и содержательной связью с субъективной вероятностью. С субъективной точки зрения вероятность представляет собой степень уверенности в данном событии, которая возникает у индивидуума, на основе известных ему данных. Такая точка зрения (известная как индивидуальная или оценочная вероятность) описана Яковом Бернулли [42], который определил вероятность, как степень доверия высказыванию, в истинности которого мы не можем быть полностью убеждены. Эта степень доверия зависит от тех знаний, которыми может располагать индивидуум и, следовательно, различна для разных индивидуумов. Операции с такой вероятностью лучше всего описывать, как искусство угадывать, точнее, описывать, как искусство угадывания. Неясность суждений, основанных на субъективном анализе, обусловливает и те трудности, которые возникают в применениях субъективной вероятности. Общепризнано, что постулаты субъективной вероятности не применимы во многих интересных и полезных, но не точных, теориях современной науки. Субъективную вероятность можно рассматривать, как индивидуальный способ трактовки тех аспектов объективных данных, которые доступны индивидуальному суждению. Однако такие суждения не аддитивны, так как поведение человека часто находится в противоречии с предположением теории субъективной вероятности об аддитивности мер, используемых человеком в критериях оценки событий.

Объяснение

В интеллектуальном центре подсистемы контроля и диагностики энергоустановок ТЭС – 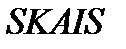работает программный модуль по схеме 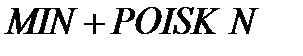. Основное назначение модуля – программное решение задач минимизации функций цели, имеющих несколько минимумов, но достаточно гладких в окрестностях каждого из них. Вдали от минимумов допускаются неустранимые разрывы первого рода. Для нахождения окрестности глобального минимума используется из 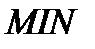метод случайного поиска (его комбинация). Методом сопряженных градиентов минимум уточняется. При появлении «оврагов» градиентные методы отказываются работать. В этом случае подключается к 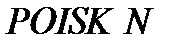овражный метод Гельфанда И.М., который позволяет осуществить многомерный поиск минимума, [Растригин Л.А.]. Из точки 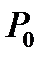по двум направлениям выполняется наискорейший спуск на «дно оврага», (рис.3.9а).

Рис.3.9а. Элемент многомерного поиска оптимума (по схеме ) :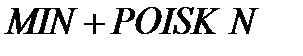

- где взять ближайшую точку – Эвристика! – ближайшая точка совпадает с .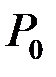

Но срабатывает помеха! Для этого, при вычислении градиента, вначале берем шаг 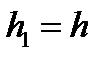, а потом шаг 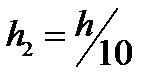, получаем точки 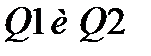, определяющие прямую линию – «дно оврага». По «дну оврага» выполняем еще один многомерный поиск минимума. Получим точку 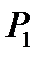. При необходимости этот элемент поиска можно повторить. Последовательность 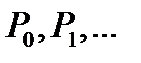задает убывающую последовательность целевой функции 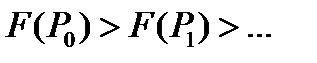. После срабатывания правила остановки, когда реализуется заданный порог похожести 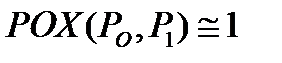, (рис. 3.9а. и ПП 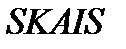с именем SIM). Последняя полученная точка 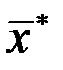и значение функции в этой точке будут точкой глобального минимума .

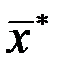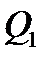Результаты анализа сравниваемых состояний представляются визуально. Порог похожести задается разработчиком -а. Точки и считаются лежащими на дне оврага (рис.3.9а). Эти две точки определяют прямую линию, по которой осуществляется одномерный поиск минимума. Одно из направлений в точке 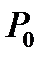является градиентным. Второе направление будет случайным. Эта комбинация, детерминированного и случайного поиска, приводит к желаемому результату. Регулирующими параметрами элемента поиска является пара ( 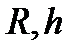), где 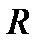- первоначальный шаг. В качестве правила остановки, при наискорейшем спуске на дно оврага и принятом механизме случайного выбора решения из полученного набора эвристик, используется принцип «похожести» точек [55]. Одной из эвристик алгоритма является предварительное знание об области 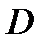и примерной зоне поиска 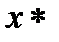, в которой находится минимум функции 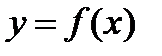, а также знание об изменении параметров технологического процесса по их «похожести» (значения 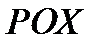должны быть одинаковыми, или близкими). Эта информация позволит оценить первоначальный шаг 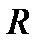и значения функции 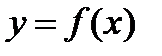в выбранных точках функциональных значений 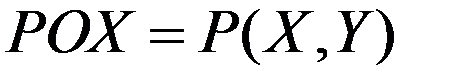на экране монитора (рис.5, табл. П.1).

Рис. 5. «Похожесть» диагностируемого состояния (при сравнении с нормативным значением 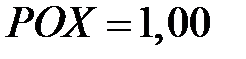) и определение фактического значения 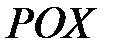(общее состояние энергоустановки) как расстояния между ними, определяемое по формуле [55]:

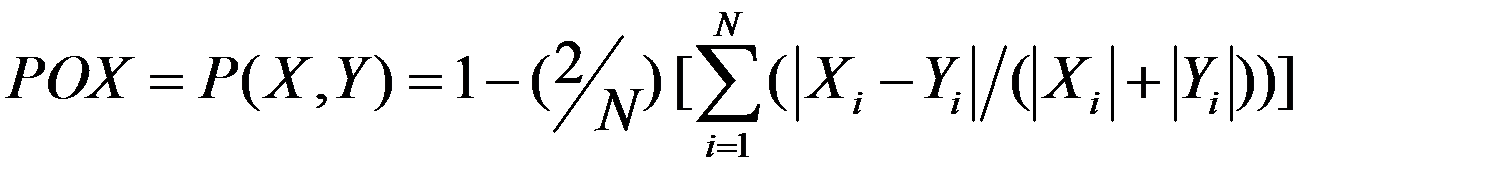,[55].

Здесь 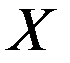- вектор измеренных параметров; 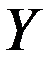- вектор эталонных значений параметров; 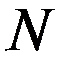- количество анализируемых параметров; 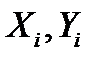- наборы значений признаков (параметров состояния) для диагностируемого ( 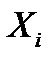) и эталонного ( 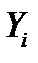) объектов (агрегатов), 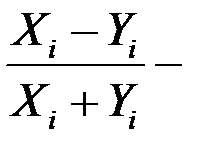коэффициент Фехнера (см. закон Вебера-Фехнера, 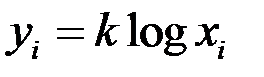, где 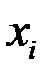- оценка некоторой величины 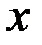при «ощущении» ).

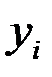При этом, 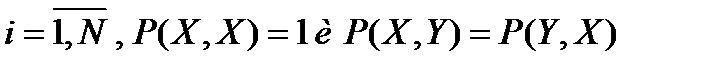. Если известно 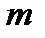элементов – эталонов 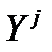, где 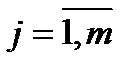, то, используя понятие «похожесть», можно найти ближайший к данному объекту 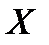(его состоянию) эталон 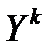по максимуму значения коэффициента 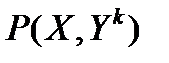, где .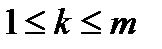

Таблица П.1

Массив «весов» параметров-признаков (отклонение мощности турбины ΔN_Э и ее экономичности Δ 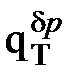от гарантийного значения, DELTA = ΔN_Э/Δ 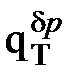) турбоустановки Т – 100 – 130 ТМЗ ст. №7 Н ТЭЦ – 4 (в отдельных опытах до и после ремонта) и сравнение параметров состояний по мере «похожесть» (РОХ). Режим работы – конденсационный.

Номинальные (гарантийные) параметры		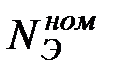		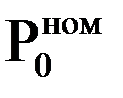		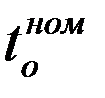		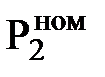	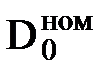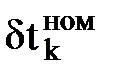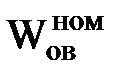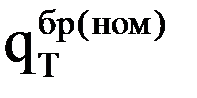РОХ	DELTA
МВт	МПа	0С	МПа	т/ч	0С	м<