Понятие о моделировании рядов наблюдений

Моделирование рядов методом статистических испытаний –процесс определения последовательности возможных значений ряда по его заданным числовым характеристикам или функции распределения путем преобразования значений случайной величины а, равномерно распределенной в интервале (9, 1).

Модель того или иного ряда представляет собой ряд заданной продолжительности N, характеристики которого при увеличении числа испытаний стремятся к характеристикам исходного ряда.

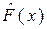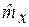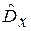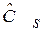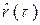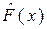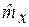Характеристики исходного ряда могут задаваться разными способами. В одном случае в качестве заданных могут выступать характеристики закона распределения , например, , , , , и т. д., рассчитанные по конкретному числовому ряду X. При моделировании эти характеристики принимаются в качестве генеральных, т. е. принимается, что F(x)= , m_x= , D_x= 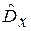, С_s = 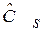, 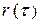= 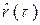. Полученный в результате моделирования ряд будет представлять собой, модель заданной продолжительности конкретного исходного ряда. В другом случае в качестве заданных могут выступать искусственно назначаемые исходя из тех или иных соображений характеристики закона распределения. В этом случае получается модель абстрактного ряда с теми или иными заданными свойствами, а сам процесс моделирования называется розыгрышем.

В зависимости от принятой математической модели исходного ряда закон распределения может быть одномерным F₁(x) (случайный ряд), двухмерным F₂(x) (простая цепь Маркова), n-мерным F_n{x) (например, сложная цепь Маркова) и т. д. Принципиальная схема моделирования во всех перечисленных случаях одинакова, однако практическая реализация ее существенно различается.

Моделирование основано на известном положении о том, что если случайная величина X имеет плотность распределения f(x), то вне зависимости от закона распределения X, распределение соответствующих X значений функции распределения

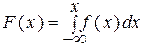(9.4)

является равномерным в интервале (0, 1).

Отсюда процедура преобразования равномерно распределенных в интервале (0, 1) случайных чисел а в случайные числа X с заданным законом распределения сводится к решению уравнения

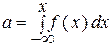(9.5)

относительно х по заданному α

В большинстве случаев уравнение (9.5) аналитически не решается. Поэтому в практических приложениях обычно использу­ются приближенные приемы определения X. К ним относятся:

— решение уравнения (9.5) посредством аппроксимации подынтегральной функции полиномами или другими функциями, обеспечивающими удобство определения X;

— определение значений функции x = f(a) по таблицам, содержащим заранее рассчитанные решения уравнения (9.5).

Наибольшее распространение в практике моделирования получил второй прием. При этом в оперативную память ЭВМ вводится, например, таблица нормированных ор­динат кривых обеспеченности Пирсона III типа 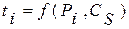или таблица модульных коэффициентов какого либо другого закона распределения 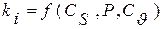и т. д. Далее одним из изложенных выше методов (см. разд. 5.4) производится генерирование значений случайной величины а. Значения а принимаются за значения обеспеченности Р в долях единицы (P=a) или в процентах (в последнем случае Р=100а). По значениям P_i из таблицы заданного закона распределения, например, 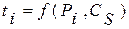последовательно считываются значения t_i которые затем по формуле (3.35) переводятся в x_i. Полученный ряд случайных зна­чений x₁, x₂, x₃ …. будет подчиняться заданному закону распреде­ления тем точнее, чем больше его объем.

Таким образом, имея некоторый ограниченный объем экспериментальных данных — п, при заданном известном или предполагаемом¹ законе распределения, можно получить практически неограниченную искусственную выборку объемом N, содержащую значительно большую информацию о возможных вариантах чередования и значениях случайной величины, отвечающей данной функции распределения.

При использовании таблиц для определения значений X следует иметь ввиду следующее обстоятельство. Значения Р и t_i или k в таблицах заданы в дискретном виде, в то время как в действительности эти величины часто являются непрерывными. Поэтому в ходе моделирования обычно требуется интерполяция (чаще всего линейная или квадратичная) между заданными в таблице значениями, которая в общем не вызывает трудностей. Сложностивозникают в том случае, когда полученные в ходе моделиро­вания значения случайной величины выходят за интервал заданных в таблице. Так, в таблице нормированных ординат биномиальной кривой обеспеченности Пирсона III типа значения Р заданы в пределах от 0,01 до 99,9 %, а при моделировании значения Р могут быть получены, например, равными 0,001 %. В этом случае нет общепринятых решений. Однако имеющийся опыт показал, что достаточную точность (с учетом того, что значения Р > 99,9 и Р < 0,01 встречаются крайне редко) можно получить путем линей­ной инелинейной экстраполяции по двум-трем предшествующим табличным значениям Р и X. Другое предложение [45] сводится к преобразованию интервала рассчитанных значений Р (0—100 %), —обозначим через Р', в табличный интервал от 0,01 до 99,9 %, —обозначим через Р, с помощью линейного равенства

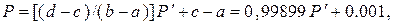(9.6)

где (b — а) — исходный интервал (0, 1); (d - с) — преобразованный интервал.

Однако это преобразование приводит к некоторому завышению малых обеспеченностей и уменьшению больших, а следовательно, занижению больших значений стока и завышению малых.

Возможно, более правильным было бы примоделировании принимать, что при всех Р<0,01 % значение х_P = x_P=0,01. Частично это обосновывается тем, что значения максимальных, средних годовых и т. д. расходов для каждой реки ограничены сверху. Известно также, что на земле не наблюдался максимум обеспеченностью (по кривой Пирсона III типа) меньше 0,3 % [50].

В то же время теоретические кривые обеспеченности, используемые в гидрологических расчетах (см. гл. 4), за исключением кривой Джонсона, не ограничены сверху и при очень малых Р по ним можно получить очень большие значения, не оправданные ни физическими соображениями, ни фактическими данными.

Есть еще ряд обстоятельств, которые не учитываются в современных методах моделирования. Это связано с тем, что влияние их сказывается очень редко. Но так как при моделировании методом Монте-Карло, как правило, стремятся получить выборки большого объема, названные редкие явления становятся вполне вероятными. В этой связи интересным, например, является вопрос о числе знаков после запятой в значении а и, следовательно, в обеспеченности Р. Например, если в значении Р, измеренного в процентах, учитывать пять знаков после запятой, то вполне вероятно, что при моделировании потребуется определять значение X обеспеченностью в одну стотысячную долю процента. Если же после запятой взять три знака, то при моделировании длинной выборки потребуется найти значение X обеспеченностью в одну тысячную долю процента. Разница между первым и вторым случаем весьма существенная.

¹ Оговорка существенна. Часто закон распределения носит гипотетический характер, и метод Монте-Карло используется для последующего определения именно закона распределения.