Принципы построения конечно-элементных моделей

Расчетная схема представляет собой идеализированную модель конструкции. Модель разбивается на конечные элементы. В результате такой разбивки появляются узлы. Элементы и узлы схемы нумеруются. В опорные узлы следует ввести соответствующие связи (запретить перемещения по каким-либо степеням свободы, либо ограничить перемещения узла конечными элементами, моделирующими работу связи). Нумерация узлов и элементов определяет последовательность задания исходной информации на входном языке и чтение результатов счёта. Конечные элементы, имеющие одинаковые жёсткостные характеристики, объединяются в типы жесткости.

Расчетная схема располагается в правой декартовой системе координат.

Для фиксации местоположения конечного элемента в схеме служит местная система координат - C1, U1, Z1, которая является только правой декартовой. Местная система координат необходима для ориентации местной нагрузки, главных осей инерции в сечении стержня, усилий и напряжений, возникающих в элементе.

Для стержневых КЭ местная система координат имеет следующую ориентацию: ось C1 направлена от начала стержня (первый узел) к концу (второй узел). Оси U1 и Z1 - это главные центральные оси инерции поперечного сечения стержня и вместе с осью C1 образуют правую тройку. При этом ось Z1 направлена всегда в верхнее полупространство, а ось U1 параллельна плоскости COU.

Однако для построения местной системы координат для стержня в общем случае этого недостаточно. Если одна из осей сечения стержня в реальной конструкции не параллельна плоскости C0U, то необходимо задавать угол чистого вращения - угол поворота главных осей инерции относительно положения, принятого по умолчанию (см. п. 9.6).

Для всех плоскостных КЭ ось C1 направлена от первого узла ко второму. Для прямоугольных элементов плиты и оболочки ось U1 направлена от первого узла к третьему. Для плосконапряженных элементов от первого узла к третьему направлена ось Z1. Для треугольных элементов плиты и оболочки ось U1 ортогональна оси C1 и расположена в плоскости элемента. Для плосконапряженных треугольных элементов ось Z1 ортогональна оси C1 и расположена в плоскости элемента.

Для объёмных конечных элементов ось C1 направлена от первого узла ко второму, ось U1 располагается в плоскости нижней грани и ортогональна оси C1. Оси C1, U1, Z1 образуют правую тройку.

Каждый узел схемы имеет свою локальную систему координат - C2, U2, Z2, которая является правой декартовой. По умолчанию локальная система координат узла совпадает с глобальной. Локальная система координат узла позволяет задавать нагрузки и заданные смещения в направлении, не совпадающем с глобальными осями.

Каждый узел схемы в общем случае имеет 6 степеней свободы: три линейных перемещения вдоль осей C или C2; U или U2; Z или Z2 и три поворота вокруг C или C2, U или U2, Z или Z2.

Для расчетных схем, в которых количество степеней свободы в узле заведомо меньше 6 (плоские фермы, плоские рамы и т.п.), применяется так называемый признак схемы. В ПК ЛИРА задействованы пять признаков схемы:

Признак 1 – схемы, располагаемые в плоскости XOZ; каждый узел имеет 2 степени свободы - линейные перемещения вдоль осей X, Z или X2, Z2. В этом признаке схемы рассчитываются плоские фермы и балки-стенки.

Признак 2 – схемы, располагаемые в плоскости XOZ; каждый узел имеет 3 степени свободы - линейные перемещения вдоль осей X, Z или X2, Z2 и поворот вокруг оси Y или Y2. В этом признаке схемы рассчитываются плоские рамы и допускается включение элементов ферм и балок-стенок.

Признак 3 – схемы, располагаемые в плоскости XOY; каждый узел имеет 3 степени свободы - линейное перемещение вдоль оси, Z или Z2 и повороты вокруг осей X, Y или X2, Y2. В этом признаке рассчитываются балочные ростверки и плиты; допускается учет упругого основания.

Признак 4 – пространственные схемы, каждый узел которых имеет 3 степени свободы - линейные перемещения вдоль осей X, Y, Z или X2, Y2, Z2. В этом признаке рассчитываются пространственные фермы и объемные тела.

Признак 5 – пространственные схемы общего вида с 6 степенями свободы в узле. В этом признаке схемы рассчитываются пространственные каркасы, оболочки и допускается включение объемных тел, учет упругого основания и т.п.

Граничные условия в расчетной схеме могут быть заданы непосредственно на узел, а также смоделированы при помощи связей конечной жёсткости. Последнее особенно эффективно, если в налагаемых связях необходимо определить реакции. При этом следует иметь в виду, что введение связей, жесткости которых значительно превосходят жесткость элементов системы, может снизить точность счета. Если же жесткость вводимых связей невелика, могут быть некоторые искажения истинного решения для внешне статически определимых систем. Рекомендуется, чтобы величина жесткости вводимых связей была на порядок - два больше самой большой погонной жесткостной характеристики из всех элементов системы. Но в каждом отдельном случае нужна индивидуальная оценка.

Статистические воздействия задаются в виде сосредоточенных сил и моментов как в узлы схемы (узловая нагрузка) по направлениям осей глобальной и локальной систем координат, так и на элементы (местная нагрузка) по направлениям местной или глобальной систем координат.

Динамические воздействия задаются в виде узловых нагрузок, действующих вдоль осей глобальной или локальной систем координат. Веса масс сооружения задаются как собственный вес конструкций, оборудования и т. п.; при этом допускается использование как местных, так и узловых нагрузок.

Действие одной нагрузки или группы нагрузок может быть объявлено как отдельное загружение - статическое или динамическое. При наличии нескольких загружений может быть произведен выбор наиболее опасных их сочетаний, которые формируют так называемые расчетные сочетания усилий (РСУ), необходимые при конструировании элементов схемы.

Реализована возможность формирования весов масс для динамического воздействия непосредственно из какого-либо статического загружения.

При создании расчетной схемы могут быть задействованы различные системы единиц измерения. Основными единицами являются единицы длины (L), силы (F), размеров сечений (S), температуры (t ).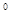

Единицы измерения прочих величин являются производными от основных.

Единица измерения времени - секунда.

Базовыми единицами, используемыми по умолчанию, являются:

L – метры, S- сантиметры, F - тонны силы, t 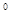- градусы Цельсия. Расчетные процессоры осуществляют расчет, используя именно эти единицы. Перевод из исходных единиц в базовые производится автоматически.

Представляя расчетную схему сооружения в виде конечно-элементной модели, пользователь всегда стремится достичь компромисса между двумя противоречивыми желаниями: получить как можно более точное решение задачи и обусловить приемлемое время счета. Желательно также получить обозримый объем результатов. Для достижения такого компромисса необходимо уметь оценивать оба указанных фактора. Так, время решения задачи легко прогнозируется по количеству узлов, элементов, загружений, а также быстродействию компьютера. ПК ЛИРА автоматически дает прогноз времени решения задачи для всех этапов расчета. Однако оценка точности решения задачи является вопросом очень сложным, так как зависит от многих слабо формулируемых факторов:

· густота сетки – с одной стороны, сгущение сетки повышает точность, с другой стороны, неограниченное сгущение может повлечь слабую обусловленность матрицы канонических уравнений и потерю точности;

· физико-механические свойства расчетной модели – расчетная схема может быть близка к геометрически изменяемой, содержать элементы с сильно различающимися жесткостями, что также влечет потерю точности;

· геометрия конечных элементов – если стороны элементов сильно различаются по длине, то это приведет к плохой обусловленности матрицы накопленных уравнений и также к потере точности;

· свойство конечных элементов – использование высокоточных элементов часто приводит к более точному решению, чем использование простых элементов на значительно более густой сетке.

Назначение сетки надо проводить на основе многих факторов. Так, например, густоту сетки предпочтительно увеличивать только в местах предполагаемого большого градиента напряжений (входящие узлы, места сосредоточенных нагрузок и т.п.). Кроме того, знание свойств конечных элементов также часто помогает рационально построить конечную модель. Так, например, на рис 9.1.а конечно-элементная модель более рациональна, чем на рис 9.1.б. Дело в том, что при моделировании перемычки, работа которой близка к балочной схеме, более предпочтительно производить ее разбивку по длине, т.к. прямоугольный конечный элемент балки-стенки имеет полилинейный закон аппроксимации функций, что автоматически моделирует закон плоских сечений, даже если по высоте балки расположен только один элемент.

а) б)

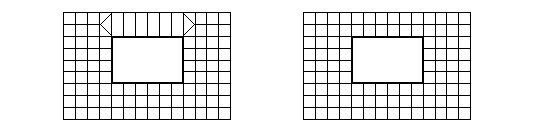
Рис.9.1

Особенно тщательно необходимо подходить к построению конечно-элементной модели в том случае, если схема рассчитываемого сооружения обладает свойствами, провоцирующими неустойчивый счет. Это относится к пологим мембранам, к конструкциям с гибкими включениями, с элементами, имеющими малые размеры, но большую жесткость.

Рекомендуется стремиться к сокращению размерности решаемой задачи. В какой-то степени может помочь применение суперэлементов. В этом случае пользователь, объявляя суперэлементом небольшой фрагмент, включающий неблагополучные элементы, может несколько сгладить их негативное влияние.

Геометрия конечных элементов также оказывает существенное влияние на точность решения задачи. Рекомендуется стремиться к тому, чтобы элементы были близки к равносторонним.

В ряде случаев пользователь может получить оценку точности решения задачи при заданной густоте расчетной сетки и определить область точного решения задачи. Зная порядок сходимости для принятого типа конечного элемента [10],можно поступить следующим образом.

Оценка сходимости для определенного типа конечного результата имеет вид:

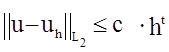, (9.1)

где левая часть неравенства является по сути аналогом квадратичной невязки между точным решением U и приближенным U_h (для определенности рассматриваем только перемещения, так как для напряжений предлагаемая схема рассуждений полностью аналогична); в правой части неравенства С-константа, h-размер элемента при заданной густоте сетки и t-порядок сходимости. Так, например, если для прямоугольных элементов балки стенки t=2 (порядок сходимости t для конечных элементов, используемых в ПК ЛИРА, приведен в [10]), можно заключить, что при сгущении сетки в два раза (т.е. при уменьшении h в два раза), погрешность решения уменьшается в 4 раза.

Теперь на основе двух решений с начальной и "удвоенной густотой" сетки можно приблизиться к точному решению.

Пусть перемещение выбранного узла с начальной густотой сетки h равно

U_i (h) = 4.8 мм

Это же перемещение при сгущении сетки в два раза

U_i (h) = 5.2 мм

Теперь можно построить ряд для определения точного значения U_i

U_i = 4.8 + 0.4 + 0.4/4 + 0.4/16 + 0.4/32 + 0.4/64 + ...

Приведенные выше рассуждения целесообразно проводить при решении сложных исследовательских задач. Для достаточно простых задач, когда количество узлов не превышает нескольких тысяч, методы, реализованные в ПК ЛИРА, позволяют получать вполне приемлемую точность на произвольных сетках, в том числе и полученных на основе автоматической разбивки.