Программный комплекс для расчета
ПРОГРАММНЫЙ КОМПЛЕКС ДЛЯ РАСЧЕТА
И ПРОЕКТИРОВАНИЯ КОНСТРУКЦИЙ
ЛИРА
Версия 9.0
Руководство пользователя
КНИГА 1
КРАТКОЕ ОПИСАНИЕ МЕТОДА КОНЕЧНЫХ ЭЛЕМЕНТОВ ДЛЯ ЛИНЕЙНЫХ ЗАДАЧ.
Общие положения
Теоретической основой ПК ЛИРА является метод конечных элементов (МКЭ), реализованный в форме перемещений. Выбор именно этой формы объясняется простотой ее алгоритмизации и физической интерпретации, наличием единых методов построения матриц жесткости и векторов нагрузок для различных типов конечных элементов, возможностью учета произвольных граничных условий и сложной геометрии рассчитываемой конструкции. Принципы построения конечно-элементных моделей изложены в главе 9.
Реализованный вариант МКЭ использует принцип возможных перемещений
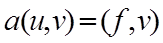 (1.1)
(1.1)
где u - искомое точное решение; v - любое возможное перемещение;
a (u,v), (f,v) - возможные работы внутренних и внешних сил.
Занимаемая конструкцией область разбивается на конечные элементы Wr, назначаются узлы и их степени свободы Li (перемещения и углы поворота узлов).
Степеням свободы соответствуют базисные (координатные, аппроксимирующие) функции mi, отличные от нуля только на соответствующих звездах элементов и удовлетворяющие равенствам
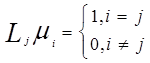 (1.2)
(1.2)
Приближенное решение Uhищется в виде линейной комбинации базисных функций
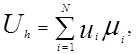 (1.3)
(1.3)
удовлетворяющей главным (кинетическим) условиям,
где: ui - числа; N - количество степеней свободы.
Далее излагается МКЭ для линейных задач, поскольку решение нелинейных задач сводится к последовательности линейных.
Подставляя в (1.1) UhвместоUи mj (j=l,...,N) вместо V, получим систему уравнений МКЭ:
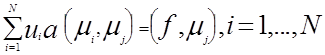 (1.4)
(1.4)
Обозначив К матрицу жесткости с элементами ki, j=a(mi, mj) , P - вектор нагрузок, с элементами Pi =(f, mi) и Х- искомый вектор с элементами ui , запишем систему (1.4) в матричной форме
КХ=Р (1.5)
Таким образом, применение МКЭ сводит задачу к системе линейных алгебраических уравнений (1.5).
Решив ее, находим вектор X , затем из (1.3) - остальные компоненты напряженно-деформированного состояния.
Важным преимуществом излагаемого метода является то, что матрицу Ки вектор Рполучают суммированием соответствующих элементов матриц жесткости и векторов нагрузок, построенных для отдельных конечных элементов.
Для МКЭ в перемещениях известны условия сходимости и оценки погрешности. Условиями сходимости являются линейная независимость и полнота системы базисных функций, а также их совместность (конформность), либо условия, компенсирующие несовместность. Совместность означает, что все базисные функции являются возможными перемещениями. Линейная независимость следует из (1.2). Известны легко проверяемые условия, позволяющие установить полноту базисных функций, их совместность или выполнение условий, компенсирующих несовместность. Эти условия имеют вид равенств, которым должны удовлетворять базисные функции на каждом конечном элементе. Такая теоретическая основа позволяет не только исследовать корректность применения известных конечных элементов, но и разработать принципы конструирования новых совместных и несовместных элементов и получить для них оценки погрешности.
Библиотека конечных элементов (БКЭ) содержит элементы, моделирующие работу различных типов конструкций:
· элементы стержней,
· четырехугольные и треугольные элементы плоской задачи, плиты, оболочки,
· элементы пространственной задачи - тетраэдр, параллелепипед, трехгранная призма.
Кроме того, в библиотеке имеются различные специальные элементы, моделирующие связь конечной жесткости, упругую податливость между узлами, элементы, задаваемые численной матрицей жесткости.
Все конечные элементы, включенные в библиотеку, теоретически обоснованы, для них получены оценки погрешности по энергии и по перемещениям. Погрешность по энергии оценивается величиной, пропорциональной ht, где h – максимальный из размеров конечных элементов, t =2 для прямоугольных и четырехугольных элементов плиты, t =1 для остальных элементов. Погрешность по перемещениям оценивается величиной, пропорциональной ht, где t=4 для совместных прямоугольных и четырехугольных элементов плиты, t=2 для остальных элементов. Теоретически обоснована также возможность задания криволинейных стержней прямолинейными элементами и произвольных оболочек треугольными и прямоугольными (для цилиндрических оболочек) элементами плоской оболочки. Погрешность по энергии и перемещениям оценивается в этом случае величиной, пропорциональной h.
ПРИНЦИПЫ ОПРЕДЕЛЕНИЯ РАСЧЕТНЫХ СОЧЕТАНИЙ УСИЛИЙ (РСУ)
В общем случае напряженно-деформированного состояния тела критерием для определения опасных РСУ служат экстремумы упругого потенциала в какой-либо точке тела при действии на него многих загружений. При этом учитываются особенности упругого потенциала, характерные для стержней, пластин, оболочек и массивных тел. Эти особенности позволяют облегчить решение задачи, существенно ограничив количество рассматриваемых РСУ.
Стержни
В качестве критерия определения РСУ здесь приняты экстремальные значения нормальных и касательных напряжений в контрольных точках сечения (рис. 5.1).
Для нормальных напряжений применяется следующая формула:
 (5.1)
(5.1)
где: k- точка сечения стержня (k = 1¸ 9).

Рис. 5.1
Эта формула преобразуется следующим образом при

 (5.2)
(5.2)
где: Яyiи Яzi- ядровые расстояния в сечении стержня (i=1,2).
Такой подход позволяет определить экстремальные нормальные напряжения в сечении любой формы, приведя ее к прямоугольной.
Для касательных напряжений используется приближенная формула:
 (5.3)
(5.3)
Формулы вычисления экстремальных значений для каждой точки сечения приведены в табл.5.1, а нумерация «критериальных» значений и соответствующих им напряжений - в табл. 5.2. В таблице 5.1 используется принятое правило знаков для усилий.
Кроме экстремальных напряжений вычисляются также экстремальные значения продольной и перерезывающих сил.
Всего для сечения стержня отбирается 34 значений РСУ.
Таблица 5.1
| № точки сечения | Нормальные напряжения | Касательные напряжения сечения |
| sF = N + My /Яz2 + Мz /Яy1 | — | |
| sF = N + Му /Яz2 - Mz /Яy2 | — | |
| sF=N - My/Яz1 - Мz/Яу2 | — | |
| sР=Н - Му/Яz1 +Мz/Яу1 | — | |
| sF=N+Mz/Яy1 |  | |
| s=М - Мz/Яу2 |  | |
| sF=N+Мy/Яz2 |  | |
| s=N - Mу/Яzl |  |
Таблица 5.2
| Критерии и их значения. | ||||||||||
| №№ критериев | ||||||||||
| Значение | s1 + | s1 - | s2 + | s2 - | s3 + | s3 - | s4 + | s4 - | t7 + | t7 - |
| №№ критериев | ||||||||||
| Значение | t8 + | t8 - | t5 + | t5 - | t6 + | t6 - | N+ | N - | s7 + | s7 - |
| №№ критериев | ||||||||||
| Значение | s8 + | s8 - | s5 + | s5 - | s6 + | s6 - | Qy+, N+ | Qy-, N+ | Qy+, N- | Qy-, N- |
| №№ критериев | ||||||||||
| Значение | Qz+, N+ | Qz-, N+ | Qz+, N- | Qz-, N- |
Плиты
Здесь применяется подход, аналогичный тому, который описан в п. 5.2. Изгибные и крутящий моменты в плите дают возможность определить нормальные и касательные напряжения на верхней и нижней поверхностях плиты. Эти напряжения по модулю равны, поэтому формулы (5.4) и (5.5) приобретают вид
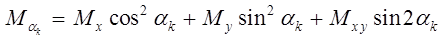 (5.6)
(5.6)
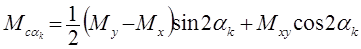 (5.7)
(5.7)
Оболочки
Здесь также применяется аналогичный подход. Напряжения вычисляются на верхней и нижней поверхностях оболочки. При этом учитываются мембранные напряжения и изгибающие усилия по следующим зависимостям:
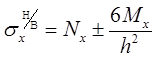
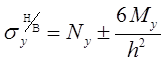
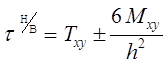 (5.8)
(5.8)
где: h - толщина оболочки;
ВиН — индексы, означающие принадлежность к верхней и нижней поверхностям. Шаг просмотра угла.a = 10°.
Объемные элементы
Критерием для определения опасных сочетаний напряжений в общем случае НДС приняты экстремальные значения среднего напряжения (гидростатического давления) и главных напряжений девиатора. Определяются углы наклона главных напряжений в каждом элементе для каждого загружения. Вычисление производится по формулам:
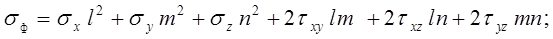
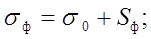 (5.9)
(5.9)
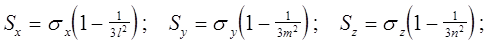
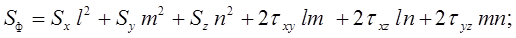
где :
sф - нормальное напряжение на площадке с направляющими косинусами l, т, п к осям XI, YI, ZI;
Sф - нормальное напряжение девиатора на этой же площадке;
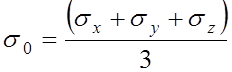 - среднее напряжение.
- среднее напряжение.
Процесс выбора организован следующим образом. Для данного элемента вычисляются направляющие косинусы главных площадок по всем загружениям. Если в схеме задано n загружений, то будет найдено Зn площадок. Затем вычисляются напряжения Sф на этих площадках от всех загружений и производится накопление положительных и отрицательных значений напряжений.
В соответствии с этим принято обозначение критериев как трехзначных чисел. Первые две цифры обозначают порядковый номер загружения, на площадках которого вычисляются напряжения от всех загружений. Третья цифра может принимать значения от 1 до 6, которым придается следующий смысл:
1 - положительное суммарное значение напряжения на 1-ой главной площадке;
2 - отрицательное суммарное значение напряжения на 1-ой главной площадке;
3 и 4- то же на 2-ой главной площадке;
5 и 6- то же на 3-ей главной площадке.
Так, например, критерий 143 означает, что на 2-ой главной площадке 14-го загружения получено наибольшее положительное значение напряжения. Критерий 076 означает, что на 3-ей главной площадке 7-го загружения получено наибольшее отрицательное значение напряжения.
Критерии, соответсвующие наибольшему и наименьшему значениям среднего напряжения, обозначаются цифрами 7 и 8 соответственно.
Загружения
При определении РСУ учитываются логические связи между загружениями, которые отражают физический смысл загружений и требования, регламентируемые различными нормативными документами. Выделяются три типа загружений:
· независимые (собственный вес, вес оборудования и т.п.);
· взаимоисключающие (ветер слева и ветер справа, сейсмическое воздействие вдоль разных осей координат и т.п.);
· сопутствующие (тормозные при наличии вертикальных крановых нагрузок и т.п.).
Предоставляется также возможность обозначить знакопеременность загружения при одинаковом модуле его вектора.
РАСЧЕТ НА УСТОЙЧИВОСТЬ
Реализованный вариант расчета на устойчивость предполагает, что распределение сил Nо известно из линейного расчета. Требуется найти значение числового параметра lо такое, чтобы при силах (lо * Nо) произошла потеря устойчивости.
Задача определения критических сил и соответствующих им форм потери устойчивости допускает следующую вариационную формулировку: найти перемещение и ¹ 0 и число lо такие, что при всех допустимых перемещениях vсправедливо равенство:
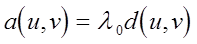 (6.1)
(6.1)
где d(u,v ) - возможная работа сил при заданном их распределении No.
Пользуясь выражением (1.3) и обозначив D матрицу с элементами 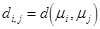 , получим из (6.1) задачу на собственные значения для матриц
, получим из (6.1) задачу на собственные значения для матриц
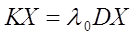 (6.2)
(6.2)
Погрешность МКЭ в задаче устойчивости для критических сил и соответствующих им форм потери устойчивости пропорциональна ht .
Решение производится методом половинного деления. Этот метод основан на том, что матрица 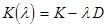 положительно определена лишь при l<l0. Отсутствие положительной определенности матрицы соответствует наличию отрицательных чисел на главной диагонали после исключений по методу Гаусса.
положительно определена лишь при l<l0. Отсутствие положительной определенности матрицы соответствует наличию отрицательных чисел на главной диагонали после исключений по методу Гаусса.
После определения с заданной точностью параметра l0 форма потери устойчивости находится как собственный вектор матрицы K(λ0)  методом итерации подпространств, изложенным в п.3.
методом итерации подпространств, изложенным в п.3.
Расчет реализуется в упругой стадии. Значения сжимающих сил и напряжений в элементах схемы уже вычислены с помощью линейного процессора. При выполнении расчета на устойчивость предполагается, что эти значения выражены через критический параметр нагрузки:
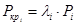
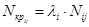
где
i - номер загружения;
j - номер элемента в схеме;
Pi- суммарная нагрузка в i-том загружении;
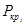 - критическая нагрузка в i-том загружении;
- критическая нагрузка в i-том загружении;
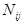 - продольное усилие или напряжение в j-том элементе в i-том загружении;
- продольное усилие или напряжение в j-том элементе в i-том загружении;
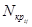 - критическое продольное усилие в j-том элементе в i-том загружении;
- критическое продольное усилие в j-том элементе в i-том загружении;
li - параметр нагрузки (коэффициент запаса устойчивости).
В процессе счета для каждого загружения определяются первая форма потери устойчивости и соответствующий ей коэффициент запаса.
Допускается также производить проверку устойчивости по линейным комбинациям загружений (РСН).
Если в расчете схемы присутствуют динамические загружения, то проверка устойчивости схемы для них может быть произведена только через комбинации загружений (РСН). Это связано с тем, что разложенные по формам колебаний результаты расчета на динамическое воздействие необходимо преобразовать в суммарные.
В процессе расчета общей устойчивости итерационным методом определяется значение lтакое, при котором хотя бы один элемент диагонали матрицы жесткости обращается в ноль. Если li ³1, то считается, что схема устойчива в данном загружении или при данной комбинации загружений.
В качестве исходных данных задаются V начальный масштабный множитель к продольным силам Ni ( по умолчанию V=2) , а также точность вычислений (по умолчанию равна 0.01). Предполагается, что при li>V система абсолютно устойчива.
В результате вычисляются коэффициенты запаса устойчивости li, первая форма потери устойчивости и коэффициенты свободной длины для стержневых элементов, исходя из общей устойчивости, по следующим формулам:
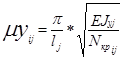 (6.3)
(6.3)
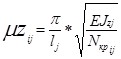 , где:
, где:
myij, mzij – коэффициенты свободной длины j-того стержня
соответственно в плоскостях X1oZ1, X1oY1
для i-того загружения;
EJyj, EJzj– изгибные жесткости j-того стержня соответственно в
плоскостях соответственно X1oZ1, X1oY1;
Nкрij = li*Nij - критическое продольное усилие сжатия в j-том стержне
для i-того загружения;
li – коэффициент запаса устойчивости для i-того загружения;
lj - длина j-того стержня.
РЕШЕНИЕ НЕЛИНЕЙНЫХ ЗАДАЧ
Общие положения
Нелинейный процессор предназначен для решения физически и геометрически нелинейных, а также контактных задач.
В линейных задачах существует прямая пропорциональность между нагрузками и перемещениями вследствие малости перемещений, а также между напряжениями (усилиями) и деформациями в соответствии с законом Гука. Поэтому для линейных задач справедлив принцип суперпозиции и независимости действия сил.
В физически нелинейных задачах отсутствует прямая пропорциональность между напряжениями и деформациями. Материал конструкции подчиняется нелинейному закону деформирования. Закон деформирования может быть симметричным и несимметричным – с различными пределами сопротивления растяжению и сжатию.
В геометрически нелинейных задачах отсутствует прямая пропорциональность между деформациями и перемещениями. На практике наибольшее распространение имеет случай больших перемещений при малых деформациях.
В задачах конструктивной нелинейности имеет место изменение расчетной схемы по мере деформирования конструкции, например, в момент достижения некоторой точкой конструкции определенной величины перемещения возникает контакт этой точки с опорой.
Для решения таких задач нелинейный процессор организует процесс пошагового нагружения конструкции и обеспечивает решение линеаризованной системы уравнений на каждом шаге для текущего приращения вектора узловых нагрузок, сформированного для конкретного нагружения.
При решении задач конструктивной нелинейности применяется шагово-итерационный метод.
Нелинейный процессор позволяет получить напряженно-деформированное состояние для мономатериальных и для биматериальных, в частности железобетонных, конструкций.
Для решения нелинейных задач необходимо задавать информацию о количестве шагов и коэффициентах к нагрузке. Схема может содержать несколько нагружений, из которых может быть сформирована последовательность (история) нагружений.
Типы арматурных включений
Типы арматурных включений для стержневых элементов приведены в табл. 7.4. Типы арматурных включений для плоскостных элементов приведены в табл. 7.5. Тип арматурного включения для объемных элементов приведен в таблице 7.6.
Таблица 7.4
| Иденти-фикатор | Тип арматурных включений | Поле параметров |
| SA0 | Процент армирования (% арматуры от площади сечения бетона) | N - процент армирования (на 100 см. длины). Пример: /0 SA0 12/ Алгоритм: применяется только в сжато-растянутом стержне. |
| SA1 | Листовая горизонтальная арматура без защитного слоя 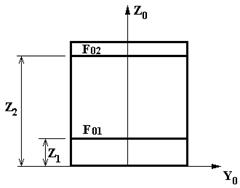 | Fai - площадь листа арматуры, dim [см. кв.]; Zi - привязка листа относительно оси Yo, dim [см. ]. Алгоритм: в типе сечения S105 при задании в стойках моделируется одним листом при дроблении DS 1 и двумя листами при дроблении DS2. |
| SA2 | Листовая вертикальная арматура без защитного слоя 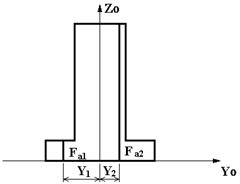 | Fai - площадь листа арматуры, dim [см. кв. ]; Yi - привязка листа относительно оси Zo, dim [см. ]. Алгоритм: в типах сечения S104, S105 при задании в пределах полок моделируется двумя листами; в типе сечения S103 допускается только в пределах стойки. |
| SA3 | Точечная арматура 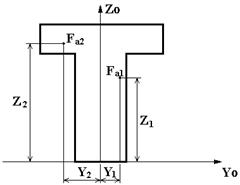 | Fai - площадь точечной арматуры, dim [cм. кв.]; Yi - привязка арматурной точки к оси Zo, dim [см. ]; Zi - привязка арматурной точки к оси Yo, dim [см. ]. |
| SA4 | Листовая горизонтальная арматура с защитным слоем, симметричная относительно оси Zo 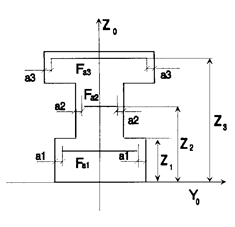 | Fai - площадь листа арматуры, dim [cм. кв.]; Ai - защитный слой, dim [cм.]; Zi - привязка листа относительно оси Yo, dim [см. ]. Алгоритм: в типе сечения S105 при задании в стойках моделируется одним листом при дроблении DSI и двумя листами при дроблении DS2. |
| SA5 | Листовая вертикальная арматура с защитным слоем, симметричная относительно горизонтальной оси симметрии сечения 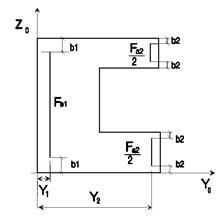 | Fai - площадь листа арматуры, dim [см. кв.]; Yi - привязка листа относительно оси Zo, dim [см.]; Bi - защитный слой, dim [см ]. Алгоритм: в типах сечения S104, S105 при задании в полках моделируется двумя листами; в типе сечения S103 допускается только в пределах стойки. |
| SA6 | Листовая горизонтальная арматура общего вида 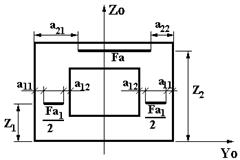 | Fai - площадь листа арматуры, dim [см. кв.]; Zi - привязка листа относительно оси Yo, dim [см.]; Ali - защитный слой левый, dim [см ]; A2i - защитный слой правый, dim [см]; Алгоритм: в типе сечения S105 при задании в стойках моделируется одним листом при дроблении DSI и двумя листами при дроблении DS2, при этом A1i - защитный слой внешних граней сечения, A2i -защитный слой внутренних граней. |
| SA7 | Листовая вертикальная арматура общего вида 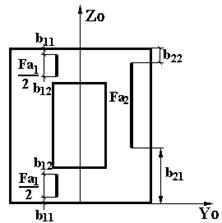 | Fai - площадь листа арматуры, dim [см. кв.]; Yi - привязка листа относительно оси Zo, dim [см. ]; Bli - защитный слой нижний, dim [см ]; B2i - защитный слой верхний, dim [см]. Алгоритм: в типах сечения S104, S105 при задании в полках моделируется двумя листами при дроблении DS2, при этом: Bli - защитный слой внешних граней сечения, B2i - защитный слой внутренних граней; в типе сечения S103 допускается только в пределах стойки. |
| SA8 | Кольцевая арматура в кольцевом сечении 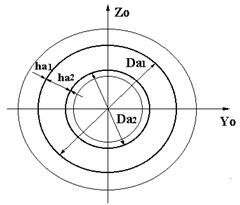 | Dai - диаметр оси кольцевой арматуры, dim [см ]; Hai - толщина кольца, dim [см.]. |
| SA9 | Точечная регулярная арматура в кольцевом сечении 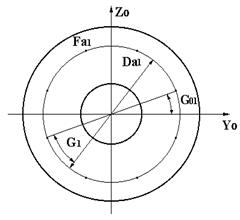 | Fai - площадь точечной арматуры, dim [см. кв.]; Dai - диаметр регулярного точечного включения, dim [см. ]; Gi - шаг сектора (угол между точками), dim [град. ]; Goi - начальная угловая привязка, dim [град.]; |
| SA10 | Точечная одиночная арматура в кольцевом сечении 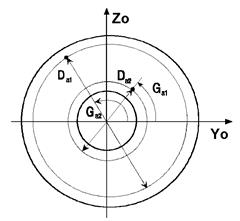 | Fai - площадь точечной арматуры, dim [см. кв.]; Dai - диаметр точечного включения, dim [см.]; Gai - угловая привязка, dim [град. ]. |
Таблица 7.5
| Иденти-фикатор | Тип арматурных включений | Поле параметров |
| SA0 | Процент армирования (отношение объема арматуры к объему конечного элемента) | a) N - общий процент армирования. б) Nх - процент армирования вдоль оси X; Nz - процент армирования вдоль оси Z. Алгоритм: Nх + Nz = N Примечание: В КЭ 221 ¸ 230 используется вариант "б", где процент армирования представляет собой отношение площади арматуры к площади поперечного сечения элемента. |
| SA1 | Арматура листового типа (физический эквивалент листа) 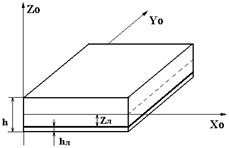 | 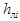 - толщина листа арматуры, dim [см ]; - толщина листа арматуры, dim [см ]; 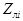 - привязка листа к серединной поверхности, dim [см]; Ограничения: до пяти листов. - привязка листа к серединной поверхности, dim [см]; Ограничения: до пяти листов. |
| SA2 | Арматура стержневого типа (физический эквивалент сетки) 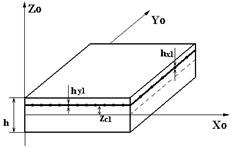 | 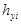 - эквивалентная толщина стержневой арматуры сетки по оси Y, dim [см ]; - эквивалентная толщина стержневой арматуры сетки по оси Y, dim [см ]; 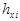 - эквивалентная толщина стержневой арматуры сетки по оси X, dim [см ]; - эквивалентная толщина стержневой арматуры сетки по оси X, dim [см ]; 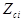 - привязка сетки к серединной поверхности, dim [см]; Ограничения: - до пяти арматурных включений. - привязка сетки к серединной поверхности, dim [см]; Ограничения: - до пяти арматурных включений. |
| SA3 | Арматура стержневого типа (физический эквивалент стержневой арматуры осевой ориентации) 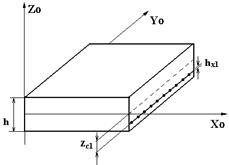 | 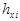 - эквивалентная толщина стержневой арматуры по оси X, dim [см ]; - эквивалентная толщина стержневой арматуры по оси X, dim [см ]; 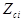 - привязка стержней к серединной поверхности, dim [см]. Ограничения: - до пяти арматурных включений; массив стержней предполагается расположенным в одной плоскости. - привязка стержней к серединной поверхности, dim [см]. Ограничения: - до пяти арматурных включений; массив стержней предполагается расположенным в одной плоскости. |
| SA4 | Арматура стержневого типа (физический эквивалент стержневой арматуры осевой ориентации) 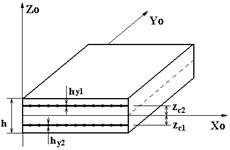 | 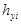 - эквивалентная толщина стержневой арматуры по оси Y, dim [см ]; - эквивалентная толщина стержневой арматуры по оси Y, dim [см ]; 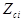 - привязка стержней к серединной поверхности, dim [см]. Ограничения: - до пяти арматурных включений; массив стержней предполагается расположенным в одной плоскости. - привязка стержней к серединной поверхности, dim [см]. Ограничения: - до пяти арматурных включений; массив стержней предполагается расположенным в одной плоскости. |
| SA11 | Арматура листового типа (физический эквивалент листа в процентах армирования) - аналог SA1 | 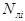 - процент армирования для i-ro листа ( в процентах к объёму конечного элемента ), dim [ % ]; - процент армирования для i-ro листа ( в процентах к объёму конечного элемента ), dim [ % ]; 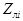 - привязка листа к серединной поверхности, dim [см]. Ограничения: - до пяти листов. - привязка листа к серединной поверхности, dim [см]. Ограничения: - до пяти листов. |
| SA12 | Арматура стержневого типа (физический эквивалент сетки в процентах армирования) - аналог SA2 | 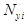 - процент армирования для i-й сетки по оси Y (в процентах к площади грани l-2K3), dim[%]; - процент армирования для i-й сетки по оси Y (в процентах к площади грани l-2K3), dim[%]; 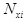 - процент армирования для i-й сетки по оси Х (в процентах к площади грани 1-ЗКЭ), dim[%]; - процент армирования для i-й сетки по оси Х (в процентах к площади грани 1-ЗКЭ), dim[%]; 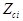 - привязка сетки к серединной поверхности, dim [см ]. Ограничения: - до пяти арматурных включений. - привязка сетки к серединной поверхности, dim [см ]. Ограничения: - до пяти арматурных включений. |
| SA13 | Арматура стержневого типа (физический эквивалент стержневой арматуры осевой ориентации в процентах армирования) - аналог SA3 | 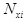 - процент армирования для i-ro включения по оси Х (в процентах к площади грани 1-3 КЭ), dim[% ], - процент армирования для i-ro включения по оси Х (в процентах к площади грани 1-3 КЭ), dim[% ], 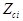 - привязка стержней к серединной поверхности, dim [см ]. Ограничения: - до пяти арматурных включений; массив стержней предполагается расположенным в одной плоскости. - привязка стержней к серединной поверхности, dim [см ]. Ограничения: - до пяти арматурных включений; массив стержней предполагается расположенным в одной плоскости. |
| SA14 | Арматура стержневого типа (физический эквивалент стержневой арматуры осевой ориентации в процентах армирования) - аналог SA4 | 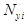 - процент армирования для i-ro включения по оси Y (в процентах к площади грани 1-2 КЭ), dim[% ]; - процент армирования для i-ro включения по оси Y (в процентах к площади грани 1-2 КЭ), dim[% ]; 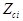 - привязка стержней к серединной поверхности, dim [см ]. Ограничения: - до пяти арматурных включений; массив стержней предполагается расположенным в одной плоскости. - привязка стержней к серединной поверхности, dim [см ]. Ограничения: - до пяти арматурных включений; массив стержней предполагается расположенным в одной плоскости. |
Таблица 7.6
| Иденти-фикатор | Тип арматурных включений | Поле параметров |
| SA0 | Процент армирования (отношение площади арматуры к площади перпендикулярного сечения элемента вдоль осей X, Y, Z) Fai = Sai/Sbi* 100%, (i=X,Y,Z), где: Sai - суммарная площадь арматуры по i-тому направлению; Sbi - площадь i - того сечения основного материала | Fx - процент армирования вдоль оси X; Fy - процент армирования вдоль оси Y; Fz - процент армирования вдоль оси Z. Алгоритм: по каждому из направлений армирования арматура учитывается раздельно со своим коэффициентом. |
Объединение перемещений
В ПК ЛИРА предусмотрена возможность задания информации об узлах, имеющих одинаковые перемещения по заданному направлению. Эти перемещения получают один порядковый номер, то есть происходит объединение нескольких неизвестных в системе линейных алгебраических уравнений.
Такой прием позволяет объединять горизонтальные перемещения узлов, принадлежащих перекрытию в плоских многоэтажных рамах, показывая тем самым, что перекрытия представляет собой жесткий диск: продольная сила, могущая возникнуть в перекрытии, ничтожно мала по сравнению с сечением перекрытия, которое её воспринимает.
Очень удобен такой приём в задачах с динамическими воздействиями от ветра или сейсмики в горизонтальном направлении. В этом случае инерционная масса всего перекрытия собирается в один (любой) узел перекрытия.
Сложнее объединять перемещения в пространстве по этажам перекрытия.
Для симметричной многоэтажной рамы, например, можно пренебречь закручиванием её вокруг вертикальной оси. Тогда достаточно объединить перемещения всех узлов перекрытия по направлениям C,U, и схема в этом случае упрощается.
Для случаев, когда центр жёсткости здания не совпадает с центром масс, а также для несимметричных в плане зданий (особенно при недостаточной расстановке диафрагм жёсткости) закручиванием здания пренебречь нельзя. Здесь следует объединять горизонтальные перемещения на уровне перекрытия по рамам. Если считать, что диск перекрытия не может изменять своей формы, то необходимо ещё и объединение перемещений для всего перекрытия по повороту относительно оси Z. Возникает необходимость учесть работу плиты перекрытия установкой, например, крестовых связей. При динамических воздействиях инерционные массы придется прикладывать к каждой из рам на уровне каждого этажа.
Уменьшить число инерционных масс можно с помощью искусственно введённых в расчетную схему траверс. Инерционная масса будет распределяться между рамами на этаже в зависимости от соотношения длины и жёсткости траверс.
Абсолютно жесткие вставки
Абсолютно жесткие вставки используются, как правило, при нарушении соосности стыковки стержней в узле: стык подкрановой и надкрановой частей колонн, примыкание к колонне ригелей разной высоты, учёт рёбер в плитах, подпёртых рёбрами и т. п.
Жесткие вставки ориентируются вдоль осей местной системы координат C1, U1, Z1. Нагрузки, задаваемые на стержень с жёсткими вставками, привязываются к началу упругой части. Заданный шарнир располагается между жёсткой вставкой и упругой частью.
Усилия вычисляются только в упругой части, поэтому при проверке равновесия в узле, где присутствует такой стержень, следует производить перенос усилий из упругой части в узел с учётом заданной нагрузки на вставку.
Угол чистого вращения
Угол чистого вращения в стержнях возникает тогда, когда направление главных центральных осей сечения не совпадает с направлением, принятым по умолчанию.
По умолчанию принята следующая ориентация местных осей:
А) для стержней общего положения (не вертикальных) ось Х1 проходит от начала к концу; ось Y1 параллельна горизонтальной плоскости XOY глобальной системы координат; ось Z1 направлена в верхнее полупространство глобальной системы координат.
Матрица направляющих косинусов вычисляется по этому правилу через координаты начала и конца стержня и имеет вид:
| глобальные \ местные | X | Y | Z | |||||
| X1 | l | m | n | |||||
| Y1(A) |  - - |  | ||||||
| Z1 |  |   |  | |||||
Здесь l, m, n – направляющие косинусы оси Х1.
При этом ширина сечения (В) по умолчанию параллельна плоскости XOY.
Угол чистого вращения F для стержня общего положения определяется следующим образом:
- начальное сечение стержня совмещается с центром глобальной системы координат;
- определяется линия пересечения плоскости начального сечения с плоскостью XOY; эту линию назовем ось А;
- направление оси А выбирается так, чтобы при взгляде с ее конца нужно было бы ось Z повернуть до совмещения с осью Х1 против часовой стрелки на угол, меньший p;
-положительный угол Fсоответствует повороту оси А до совмещения с требуемым положением оси Y1 против часовой стрелки, если смотреть с конца
оси Х1.
Если оси Y1 и А совпадают, то угол чистого вращения отсутствует.
Б) Для вертикальных стержней:
-если ось Х1 направлена снизу вверх (вдоль оси Z глобальной системы координат), то ось Y1 направлена против оси Y, а ось Z1 – вдоль оси Х. Матрица направляющих косинусов имеет следующий вид:
| Местные\ глобальные | X | Y | Z |
| X1 | |||
| Y1(A) | -1 | ||
| Z1 |
-если ось Х1 направлена вниз (против оси Z глобальной системы координат), то ось Y1 направлена против оси Y, а ось Z1 – против оси Х. Матрица направляющих косинусов имеет следующий вид:
| Местные\ глобальные | X | Y | Z |
| X1 | -1 | ||
| Y1(A) | -1 | ||
| Z1 | -1 |
Для вертикального стержня ось Апараллельна оси Y и направлена в противоположную сторону. Положительное направление угла F соответствует вращению оси А до совмещения с требуемым направлением оси Y1 против часовой стрелки, если смотреть с конца оси Х1.
Для вертикальных стержней в любом случае ширина сечения В (размер, параллельный оси Y1) параллельна оси Y глобальной системы координат, а высота сечения Н –параллельна оси Х глоба
