Справочный теоретический материал

Комплексные числа.

На множестве действительных чисел невозможно решить уравнение 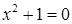. Введем условный символ 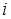, который называется «мнимая единица», основное свойство которой 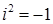, или .

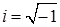Тогда числа вида 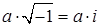назовем мнимыми числами, а числа вида 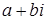– комплексными.

Комплексные числа изображают точкой на координатной плоскости.

Два комплексных числа 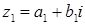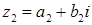равны, если равны их действительные и мнимые части: 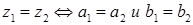. Нулем называют число 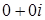, а единицей .

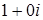Комплексные числа можно складывать по правилу:

.

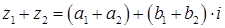Умножают комплексные числа по правилу:

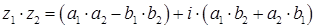
Существует обратный элемент 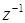, имеющий вид .

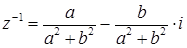Обозначим: 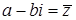– число сопряженное с z.

Тогда правило деления таково: .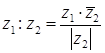

Тригонометрическая форма комплексного числа ,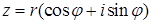

Где 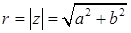– модуль комплексного числа, угол 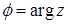– его аргумент. В тригонометрической форме комплексные числа можно умножать, возводить в натуральную степень и извлекать корень из комплексного числа по формулам:

Если 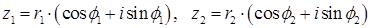, тогда

;

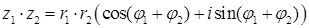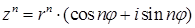- формула Муавра;

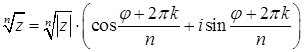, где 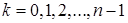к = 0,1,2,…,n-1 – формула Муавра.

На множестве комплексных чисел квадратное уравнение 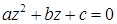имеет всегда два корня 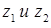. А любое уравнение 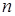-ой степени 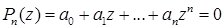имеет 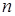корней действительных или комплексных.

Матрицы, определители и их свойства.

Прямоугольной матрицей размерности 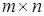называется таблица, состоящая из m строк и n столбцов.

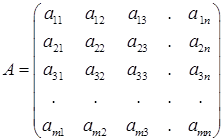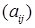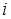= ( – номер строки, 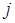– номер столбца)

Если 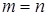, то матрица называется квадратной порядка n.

При 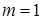– матрица строка; при 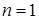– матрица столбец.

Две матрицы называются равными, если имеют одинаковую размерность и равны элементы, стоящие на одинаковых местах.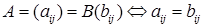

Суммой двух матриц одинаковой размерности называется матрица, составленная из сумм соответствующих элементов матриц 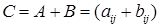. Существует нулевая матрица .

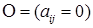Произведением матрицы 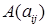на число 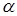называется матрица .

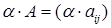Произведением матриц 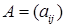размерност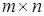и и 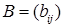размерности 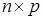называется матрица 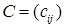, коэффициенты которой вычисляются по правилу: 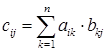. Элемент, стоящий на пересечении 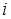-ой строки и 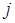-того столбца равен сумме произведений элементов 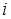-ой строки матрицы 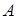на соответствующие элементы 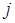-того столбца матрицы В.

Произведение матриц не коммутативно, т.е. .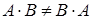

Существует 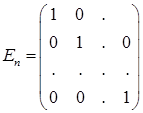– единичная матрица 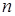- го порядка

Для матрицы 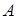размерности 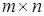выполняются свойства

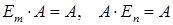. Есл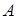и и 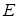квадратные матрицы одного порядка, то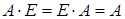

Если для данной матрицы 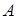существует матрица 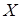: 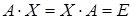, то X называется обратной A и обозначается .

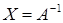Каждой квадратной матрице 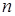-го порядка можно сопоставить число, которое называется определителем матрицы и вычисляется по определенному правилу.

Определителем второго порядка называется таблица 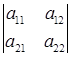, значение которого находится по правилу .

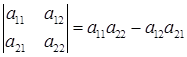Определитель третьего порядка вычисляется следующим образом: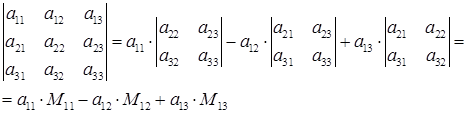

Здесь 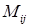– минор элемента 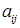т.е. определитель второго порядка, полученный из данного вычеркиванием 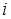- ой строки и 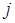- того столбца, на пересечении которых стоит данный элемент.

Определитель 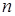- го порядка вычисляется так:

,

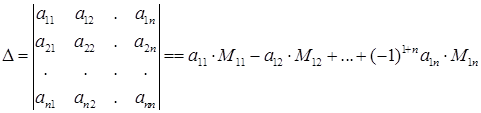где 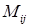- минор элемента 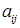т.е. определитель 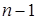- го порядка, полученный вычеркиванием 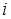- ой строки и 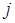- того столбца, на пересечении которых стоит данный элемент. Алгебраическим дополнением элемента 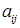назовем минор со знаком, выбранным по правилу: .

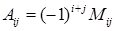Тогда 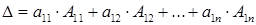. Говорят, что определитель вычислен разложением по элементам первой строки.

Перечислим некоторые свойства определителей.

1) При транспонировании матриц определители не меняются.

Под транспонированием матриц понимают преобразование матрицы (и определителя) при котором строки и столбцы меняются местами.

Следствия: а) одинаковые свойства для строк и столбцов.

б) 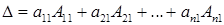– разложение по элементам первого столбца.

2) Если в квадратной матрице какие-нибудь две строки (или столбца) поменять местами, то определитель поменяет знак.

3) Определитель может быть разложен по элементам любой строки или столбца.

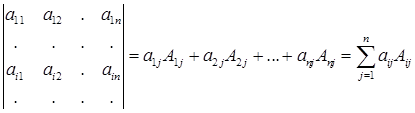
разложение по элементам 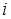– ой строки.

Следствия: а) если одна из строк (столбцов) состоит из нулей, то

определитель равен нулю.

б) если элементы строки (столбца) умножить на одно и тоже

число, то определитель умножится на это число.

4) Если определитель имеет две одинаковые строки (столбца), то он равен нулю.

5) Если матрица имеет две пропорциональные строки (столбца), то он равен нулю.

6) Определитель не изменится, если к элементам одной строки прибавить соответствующие элементы другой строки, умноженные на одно и тоже постоянное число.

Вернемся к задаче вычисления матрицы обратной данной. Сформулируем правило: всякая невырожденная матрица 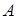(определитель 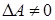) имеет обратную матрицу, которая вычисляется по формул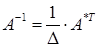е , где

матрица 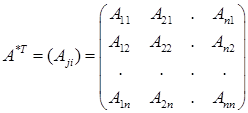составленная из алгебраических дополнений элементов данной матрицы.