Разрешенные системы линейных уравнений

Переменная 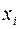называется разрешенной, если какое-нибудь уравнение системы содержит 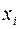с коэффициентом, равным единице, а во все остальные уравнения системы переменная 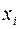не входит, т.е. входит с коэффициентом, равным нулю.

Например, система уравнений:

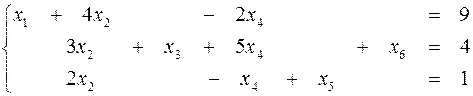
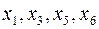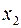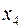содержит разрешенные переменные . Переменные и разрешенными не являются.

Если каждое уравнение содержит разрешенную переменную, то такую систему называют разрешенной. Очевидно, что приведенная в качестве примера система уравнений является разрешенной.

Выбрав из каждого уравнения разрешенной системы по одной разрешенной переменной, можно сформировать набор попарно различных переменных, который называется набором разрешенных переменных данной системы. В общем случае набор разрешенных переменных определен неоднозначно. Например, у рассмотренной выше системы можно выбрать два набора разрешенных переменных: 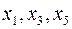и .

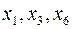Переменные системы, которые не входят в данный набор разрешенных неизвестных, называются свободными. Если в системе фиксирован набор разрешенных переменных 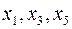, то переменные 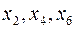являются свободными; если в набор разрешенных переменных системы входят 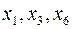, то свободными переменными являются .

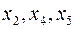Допустим, что разрешенная система уравнений содержит переменные 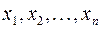,и что набор 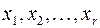является набором разрешенных переменных данной системы. Возможны два случая: 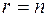и .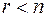

В первом случае, когда 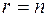, все переменные системы образуют набор разрешенных переменных системы 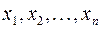. Из определения набора разрешенных переменных вытекает, что данная система содержит уравнений. Из определения разрешенных переменных следует, что переменная 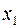содержится только в первом уравнении, переменная 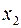– только во втором и т.д., переменная 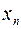– только в –м уравнении. Таким образом, разрешенная система имеет вид:

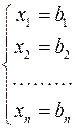
Очевидно, что такая система уравнений имеет только одно решение .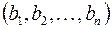

Во втором случае, когда 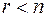разрешенная система состоит из 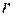уравнений вида:

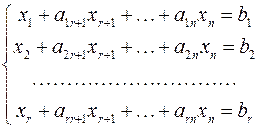
Переменные 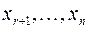являются свободными переменными системы. Если выразить разрешенные переменные системы 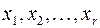через ее свободные переменные 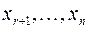, то система примет вид:

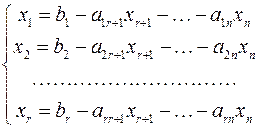
Теорема (свойство свободных переменных). Если свободным переменным системы придать 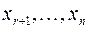произвольные значения 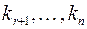, тогда:

1. можно построить решение 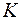системы уравнений, у которого значения свободных переменных будут равны соответственно ;

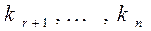2. если у решени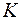й и 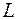системы уравнений значения свободных переменных совпадают, то и сами решения совпадают.

Доказательство: Если значения свободных переменных 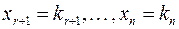подставить в систему, то получится:

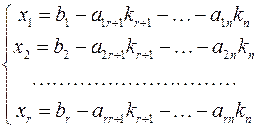
То есть:

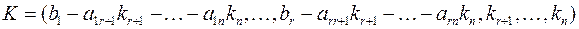является решением системы уравнений, так как после подстановки координат 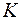в эту систему получаются верные равенства. Поскольку у 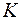значения свободных переменных равны, соответственн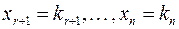о, то 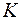– и есть искомое решение системы.

Следствие. Все решения системы получаются так же, как и решение .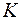

Значения для свободных переменных можно выбирать бесконечным числом различных способов, поэтому система уравнений является неопределенной.

Разрешенная система уравнений совместна всегда. Она будет определенной, если число уравнений равно числу неизвестных, и неопределенной, если число уравнений меньше числа неизвестных.

Контрольные вопросы к лекции №13

1. Критерий Кронекера-Капелли.

2. Совместные и определенные системы линейных уравнений.

3. Методы решения систем линейных уравнений и условия их применимости.

4. Однородные системы линейных уравнений.

5. Свободные и разрешенные переменные.