Тема 1. элементарная математика
Лекция 2. Элементы теории множеств
Основные понятия:
множество; элемент множества; числовые множества; конечные множества; бесконечные множества; подмножества; пустое множество; объединение множеств; пересечение множеств; разность множеств; симметрическая разность множеств; декартово произведение множеств; отображение; образ; прообраз; сюръективное отображение; инъективное отображение; биективное отображение; мощность множества.
Основные понятия
Множество – одно из важнейших понятий математики. Вводится аксиоматически и не может быть определено через какие-либо элементарные понятия.
Кантор описывает множество следующим образом:
Множество 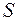 есть любое собрание определенных и различимых между собой объектов нашей интуиции и интеллекта, мыслимое как единое целое. Эти объекты называются элементами множества
есть любое собрание определенных и различимых между собой объектов нашей интуиции и интеллекта, мыслимое как единое целое. Эти объекты называются элементами множества 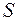 .
.
Термин «множество» характеризует совокупность, объединение некоторых объектов произвольной природы – элементов множества, которые обладают каким-либо общим для них свойством (признаком). Этот общий признак содержится в самом названии (задании) множества. Множество состоит из элементов и считается заданным, если о каждом из рассматриваемых объектов известно, входит он во множество или нет. Множество может быть задано либо перечислением его элементов, либо описанием свойств его элементов. Символическая запись 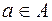 означает принадлежность элемента
означает принадлежность элемента 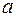 множеству
множеству  . Запись
. Запись 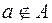 означает, что элемент
означает, что элемент 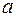 не принадлежит множеству
не принадлежит множеству  .
.
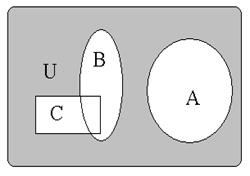 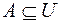 ; ; 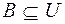 ; ; 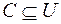 . Рис. 2.1. . Рис. 2.1. | Множество  называют подмножеством другого множества называют подмножеством другого множества 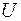 или множество или множество  включено во множество включено во множество 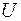 , если каждый элемент множества , если каждый элемент множества  является одновременно элементом множества является одновременно элементом множества 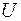 . Это обозначается . Это обозначается 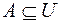 . Выделение подмножеств из множеств можно провести по различным признакам. В результате могут получиться как непересекающиеся подмножества (например, . Выделение подмножеств из множеств можно провести по различным признакам. В результате могут получиться как непересекающиеся подмножества (например,  и и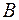 ), так и подмножества, имеющие общие элементы ( ), так и подмножества, имеющие общие элементы (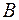 и и 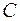 ). ). |
Если множество состоит из конечного числа элементов, оно называется конечным. При этом число элементов множества может быть очень велико или вообще неизвестно. Множество может состоять также из бесконечного количества элементов, тогда оно называется бесконечным.
Свойства включения:
1. Каждое множество есть подмножество самого себя 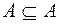 ;
;
2. Если 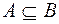 , а
, а 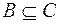 , то
, то 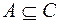 ;
;
3. 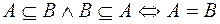 , т.е. множества
, т.е. множества  и
и  равны тогда и только тогда, когда эти множества состоят из одних и тех же элементов;
равны тогда и только тогда, когда эти множества состоят из одних и тех же элементов;
4. Каждый элемент множества  определяет некоторое подмножество множества
определяет некоторое подмножество множества  :
: 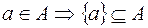 .
.
Множество, не содержащее ни одного элемента, называется пустым и обозначается 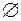 .
.
1. Любое множество содержит 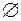 в качестве подмножества.
в качестве подмножества.
2. Каждое множество 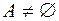 имеет, по крайней мере, два различных подмножества:
имеет, по крайней мере, два различных подмножества:  и
и 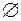 .
.
Множество  и
и 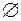 называют несобственными подмножествами множества
называют несобственными подмножествами множества  . Все остальные подмножества множества
. Все остальные подмножества множества  называются собственными или истинными. В этом случае, когда
называются собственными или истинными. В этом случае, когда 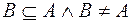 говорят, что
говорят, что 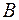 строго включено в
строго включено в  (обозначается
(обозначается 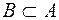 ):
):
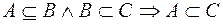
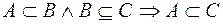
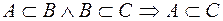
Множество всех подмножеств множества  называется множеством-степенью P
называется множеством-степенью P  множества
множества  .
.
Если  не содержит элементов, т.е.
не содержит элементов, т.е. 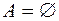 , то его единственным подмножеством является
, то его единственным подмножеством является 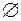 .
.
Если  – одноэлементное множество, т.е.
– одноэлементное множество, т.е. 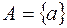 , то его подмножествами являются
, то его подмножествами являются  и
и 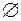 . Число этих подмножеств равно 2.
. Число этих подмножеств равно 2.
Если  – двухэлементное множество, т.е.
– двухэлементное множество, т.е. 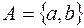 , то его подмножествами являются
, то его подмножествами являются 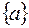 ,
, 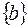 ,
,  и
и 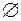 . Число этих подмножеств равно 4.
. Число этих подмножеств равно 4.
Несложно убедиться в том, что множество-степень P 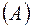 конечного
конечного  –элементного множества
–элементного множества 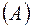 состоит из
состоит из 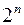 подмножеств.
подмножеств.
