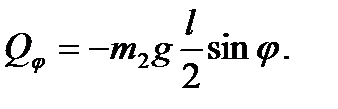Обобщенные координаты. Число степеней свободы

Пусть механическая система состоит из n точек, положение которых можно определить их 3n декартовыми координатами

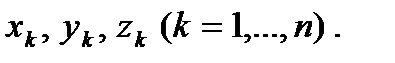
Допустим, что на систему наложено l связей, выражающихся уравнениями

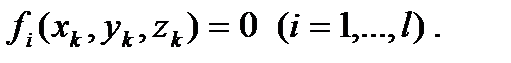
Тогда из этих уравнений l декартовых координат можно выразить через остальные s=3n-l . В результате получилось, что s декартовых координат являются независимыми и определяют положение всех точек системы. На практике удобно положение механической системы определять не декартовыми координатами точек, а некоторыми другими независимыми геометрическими параметрами, число которых будет равно s.

Независимые скалярные параметры, однозначно определяющие положение всех точек механической системы, называют обобщенными координатами Их количество s=3n-l называется числом степеней свободы механической системы.

В качестве обобщенных координат обычно выбирают некоторые углы или расстояния. При обозначении на рисунках следует указывать их геометрический смысл и положительное направление отсчета.

В дальнейшем обобщенные координаты будем обозначать 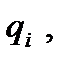где i=1,…,s.

Отметим, что независимость обобщенных координат означает, что, не нарушая наложенных связей, каждую из них можно изменять, сохраняя остальные неизменными.

Приведем несколько примеров нахождения числа степеней свободы.

Рассмотрим изображенный на рис. 31 плоский механизм, состоящий из неподвижной шестерни 1, кривошипа ОА и подвижной шестерни 2.

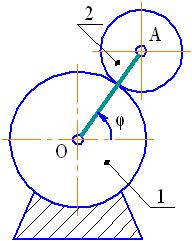
Рис. 31

В этом механизме можно двигать кривошип ОА, поворачивая его вокруг оси, проходящей через точку О. Положение кривошипа однозначно определяется углом φ ( 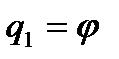), который будем отсчитывать против часовой стрелки от горизонтали до кривошипа (см. рис. 31). Если теперь величину угла φ зафиксировать (сделать кривошип неподвижным), то ни одно из тел механизма нельзя двигать, не нарушая

наложенных связей. Следовательно, одна обобщенная координата полностью определяет положение всех тел механизма и число свободы s=1.

Рассмотрим далее изображенный на рис. 32 плоский механизм, состоящий из трех грузов 1,2,3, подвижного блока 4 и двух неподвижных блоков 5,6. Тела механизма соединены нерастяжимыми нитями. Нити при движении механизма остаются натянутыми и не могут скользить по блокам, вертикальные участки нитей не раскачиваются. Здесь в качестве первой обобщенной координаты можно выбрать расстояние x от точки схода нити с блока 6 до груза 1 ( ).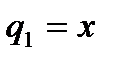

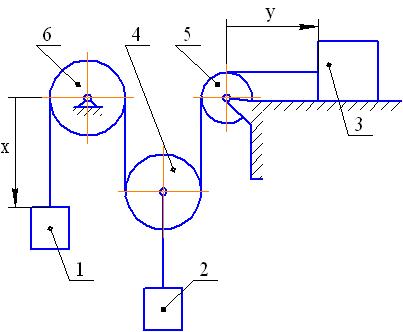
Рис. 32

Если величину x зафиксировать (сделать груз 1 неподвижным), то, не нарушая наложенных связей, можно перемещать груз 3 по опорной поверхности. При этом будут двигаться груз 2, а также блоки 4 и 5. В качестве второй обобщенной координаты можно, например, выбрать расстояние y от точки схода нити с блока 5 до груза 3 ( 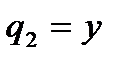). Если теперь зафиксировать две выбранные обобщенные координаты x и y, то ни одно из тел механизма нельзя будет двигать, не нарушая наложенных связей. Следовательно, в данном случае число степеней свободы s=2.

В качестве третьего примера рассмотрим стержень АВ, который может как угодно двигаться в плоскости рисунка (см. рис. 33).

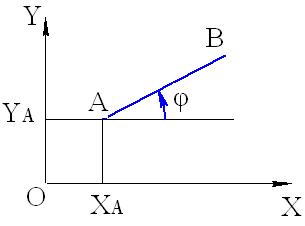
Рис. 33

Выберем в плоскости движения оси декартовой системы координат xOy. В качестве первой обобщенной координаты выберем координату x точки А 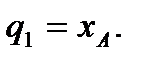Сделав координату 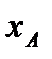неизменной, можно перемещать стержень так, чтобы точка А перемещалась по вертикали. В качестве второй обобщенной координаты выберем координату y точки А 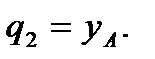Зафиксировав теперь две первых обобщенных координаты, то есть сделав точку А неподвижной, можно стержень поворачивать вокруг точки. Такое перемещение можно характеризовать углом поворота φ, который будем откладывать против часовой стрелки от положительного направления оси x до стержня АВ (см. рис. 33). Этот угол выберем в качестве третьей обобщенной координаты 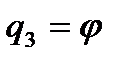. Если теперь зафиксировать все три выбранные обобщенные координаты, то положение стержня в плоскости рисунка будет однозначно определено. Следовательно, в данном случае число степеней свободы s=3.

Возможные перемещения

В аналитической механике широко используется понятие возможного перемещения. Дадим сначала определение, а затем поясним это понятие на примерах.

Возможным (виртуальным) перемещением материальной точки называется

- бесконечно малое,

- воображаемое перемещение точки,

- не нарушающее наложенных связей.

Возможным перемещением механической системы называется совокупность возможных перемещений всех ее точек.

При записи данного определения сделан акцент на трех важных признаках возможных перемещений.

Рассмотрим вначале пример, поясняющий возможное перемещение точки. Пусть на точку наложена связь, выражающаяся в том, что точка может двигаться в плоскости xOy, которую совместим с плоскостью рисунка. Возможное перемещение может быть придано точке из любого текущего положения. Изобразим траекторию движения точки под действием приложенных сил (см. рис. 34) и рассмотрим положение точки на траектории в некоторый момент времени. Из этого положения в плоскости движения точке можно придать бесчисленное множество возможных перемещений, которые представим как малое приращение радиуса-вектора точки. Обозначим возможное перемещение 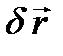. Отметим, что действительное перемещение 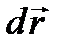, направленное по касательной к траектории в сторону движения, является одним из возможных.

Рис. 34

Возможное перемещение механической системы из какого-либо ее положения полностью определяется возможными приращениями обобщенных координат 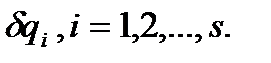Отметим, что из большого количества мыслимых возможных перемещений можно выделить независимые возможные перемещения, и любое другое возможное перемещение может быть представлено как их комбинация. Количество независимых возможных перемещений совпадает с числом степеней свободы механической системы. В качестве независимых возможных перемещений удобно выбирать такие, при которых только одна обобщенная координата 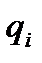получает приращение 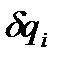, а приращения остальных обобщенных координат равны нулю:

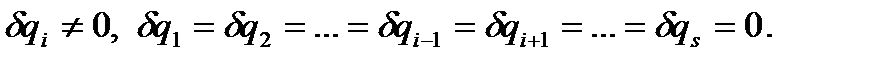
Приведем теперь пример возможного перемещения механической системы. Предварительно отметим, как следует схематически изображать возможное перемещение твердого тела, если оно входит в состав механической системы.

Если тело совершает поступательное движение, то все точки тела перемещаются на одинаковое расстояние δs в одном направлении.

При вращательном движении тела его возможное перемещение изображается как бесконечно малый поворот на угол δφ вокруг оси вращения.

Если тело совершает плоское движение, то его возможное перемещение следует изобразить как бесконечно малый поворот на угол δφ вокруг мгновенного центра скоростей (МЦС).

В каждом из этих случаев стрелкой надо указывать направление перемещения или поворота.

Рассмотрим в качестве механической системы механизм, изображенный на рис. 35. Будем считать, что при движении механизма нерастяжимые нити остаются натянутыми и прямолинейные участки нитей остаются вертикальными. В этом случае тела 1 и 4 будут совершать поступательное движение, тело 2 будет вращаться вокруг неподвижной оси и движение тела 3 будет плоским. Механизм имеет одну степень свободы. В качестве обобщенной координаты выберем расстояние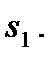

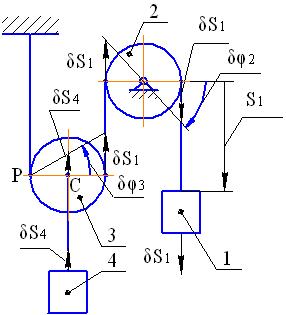
Рис. 35

Придавая механизму возможное перемещение (см. рис. 35), мысленно сместим груз 1 вниз на расстояние 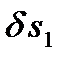. На такое же расстояние переместится точка схода нити с блока 2. Сам блок 2 повернется вокруг оси вращения на угол 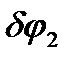по часовой стрелке. Сходящий с левой стороны блока прямолинейный участок нити переместится вверх на расстояние 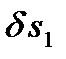. Тело 3, совершающее плоское движение, повернется вокруг МЦС, расположенного в точке схода неподвижной ветви нити, на угол 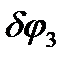против часовой стрелки. Закрепленная в точке С тела нить вместе с телом 4 поднимется вверх на расстояние 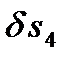. Отметим, что 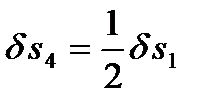исходя из подобия изображенных треугольников.

Возможная работа силы

Рассмотрим элементарную работу силы, приложенной к материальной точке, на ее возможном перемещении 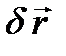. Такая работа называется возможной работой силы и обозначается 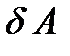. По аналогии с элементарной работой силы на действительном перемещении 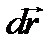возможная работа силы вычисляется по формуле (см. рис. 36)

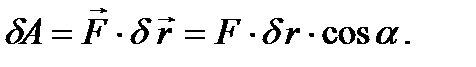(73)

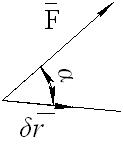
Рис. 36

Если сила приложена к телу, возможным перемещением которого является поворот на бесконечно малый угол 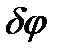вокруг неподвижной оси, то ее работу удобно вычислять по формуле

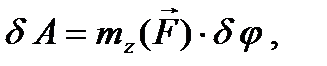(74)

где 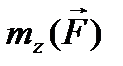- момент силы относительно оси z, направленной вдоль оси вращения в сторону вектора возможной угловой скорости 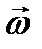(см. рис. 37). При этом вектор 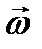следует направить в ту сторону, откуда поворот тела на угол 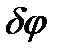виден против часовой стрелки.

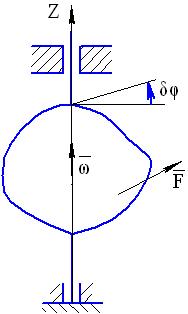
Рис. 37

Если тело может совершать плоское движение и в качестве возможного перемещения выступает поворот тела на угол 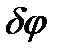вокруг мгновенного центра скоростей, то возможную работу силы, приложенной к такому телу, также удобно вычислять по формуле (74). При этом в качестве оси z следует понимать ось, проведенную через мгновенный центр скоростей перпендикулярно плоскости движения в направлении вектора возможной угловой скорости.

Отметим, что возможная работа пары сил, приложенной к некоторому телу, отлична от нуля, если возможным перемещением тела является поворот на угол 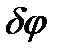вокруг какой-либо оси. Для вычисления возможной работы пары сил справедлива аналогичная формула

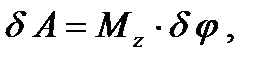(75)

где 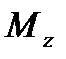- момент пары сил относительно оси z , направленной вдоль вектора возможной угловой скорости.

Обобщенные силы

Понятие обобщенной силы имеет важное значение в аналитической механике. Начнем рассмотрение этого понятия со способа вычисления обобщенной силы.

Рассмотрим механическую систему, имеющую s степеней свободы. Выберем обобщенные координаты 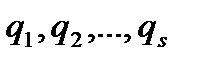, однозначно определяющие положение системы. Придадим системе возможное перемещение, при котором только одна обобщенная координата 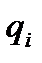получает бесконечно малое положительное приращение 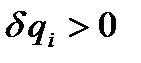(соответствующее перемещение происходит в сторону увеличения координаты 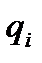), а остальные обобщенные координаты остаются неизменными. Вычислим на этом перемещении сумму работ всех сил, приложенных к точкам механической системы

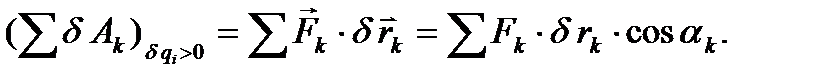
В данном случае возможные перемещения всех точек системы 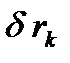могут быть выражены через 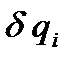и последнюю формулу можно переписать в виде

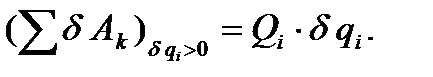(76)

Сомножитель 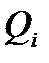перед 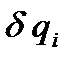в выражении (76) для суммы работ сил, приложенных к точкам механической системы, на возможном перемещении, при котором только одна обобщенная координата 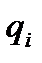получает бесконечно малое положительное приращение 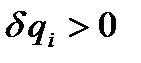, называется обобщенной силой, соответствующей обобщенной координате .

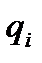Аналогичным образом можно найти обобщенную силу для каждой обобщенной координаты.

Поясним физический смысл введенного понятия.

Обобщенная сила, соответствующая обобщенной координате 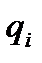, выражает суммарный эффект от действия всех сил, влияющих на изменение данной обобщенной координаты. При этом силы, входящие в выражение для обобщенной силы 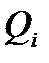со знаком плюс, способствуют увеличению обобщенной координаты 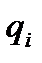, а силы, входящие в это выражение со знаком минус, препятствуют увеличению координаты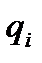

Отметим, что при нахождении обобщенных сил по формуле (76) нужно вычислять работу как внешних, так и внутренних сил, действующих на точки механической системы. Как отмечалось ранее, в реальных механических системах внутренние силы многочисленны и, как правило, неизвестны. Поэтому на практике вычисление обобщенных сил не вызывает затруднений, если сумма работ внутренних сил механической системы равна нулю на любом ее возможном перемещении. Это условие выполняется, если тела, входящие в состав механической системы, абсолютно твердые и внутренние связи идеальные. В дальнейшем при рассмотрении практических примеров будем считать, что эти условия выполняются.

Так как произведение обобщенной силы 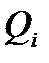на приращение обобщенной координаты 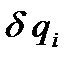является работой, то размерность обобщенной силы зависит от размерности обобщенной координаты. Если обобщенная координата имеет размерность длины, то обобщенная сила имеет размерность физической силы (в системе СИ измеряется в ньютонах). Если обобщенная координата имеет размерность угла (измеряется в радианах), то обобщенная сила имеет размерность момента силы.

Проиллюстрируем вычисление обобщенных сил на конкретных примерах.

Пример 9.

Рассмотрим механическую систему из трех тел, изображенную на рис. 38. Пусть заданы массы тел 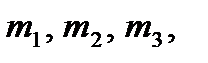радиусы 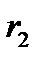и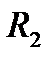

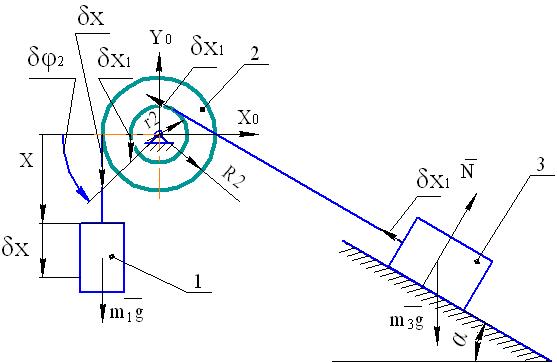
Рис. 38

ступенчатого шкива 2 и угол α. Трение отсутствует. При движении гибкие нерастяжимые нити остаются натянутыми и вертикальная нить не раскачивается. В этом случае система имеет одну степень свободы. В качестве обобщенной координаты выберем 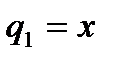(см. рис. 38). Требуется найти обобщенную силу 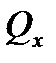, соответствующую данной обобщенной координате.

Решение

Придадим механической системе возможное перемещение, при котором обобщенная координата x получает положительное приращение 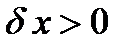. Изобразим на рис. 38 схему этого перемещения. Обозначим внешние силы, действующие на тела системы: силы тяжести тел 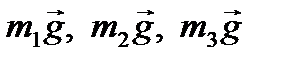, реакции шарнира О 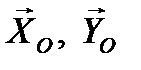и реакцию опорной поверхности 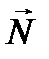. Вычислим сумму работ этих сил на изображенном перемещении

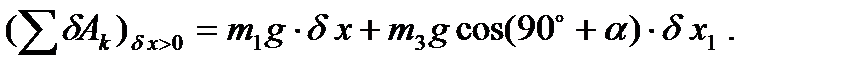(77)

Выразим перемещение 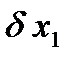через 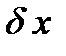исходя из подобия изображенных на рис. 38 треугольников:

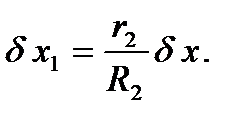
После этого выражение (77) можно переписать в виде

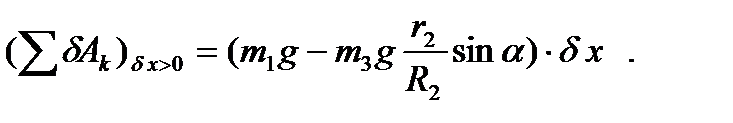
Отсюда найдем искомую обобщенную силу

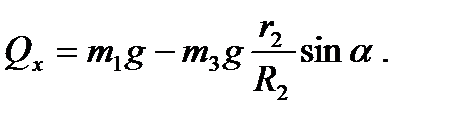
Пример 10

Рассмотрим механическую систему, состоящую из тележки массой 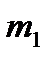и прикрепленного к ней с помощью шарнира однородного стержня ОА длиной l и массой 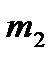(см. рис. 39). Тележка с помощью пружины,

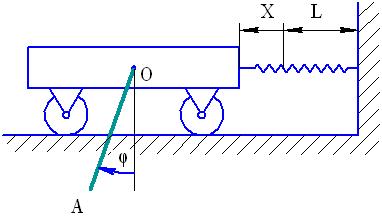
Рис. 39

коэффициент жесткости которой равен с, прикреплена к вертикальной стенке и может двигаться по горизонтальной опорной поверхности. Длина пружины в ненапряженном состоянии равна L.

Данная механическая система имеет две степени свободы. В качестве обобщенных координат выберем деформацию пружины 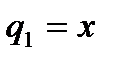и угол отклонения стержня от вертикали 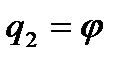(см. рис. 39).

Требуется найти обобщенные силы, соответствующие этим обобщенным координатам.

Решение

Обозначим силы, действующие на тела системы: силы тяжести 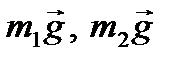, силу упругости пружины 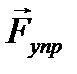и силы, действующие на колеса тележки со стороны опорной поверхности 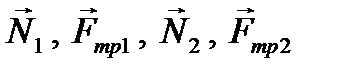(см. рис. 40).

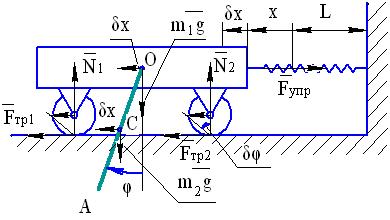
Рис. 40

Придадим механической системе возможное перемещение, при котором обобщенная координата x получает положительное приращение 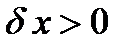, а обобщенная координата φ останется неизменной. При этом кузов тележки и стержень ОА переместятся поступательно влево на расстояние δx, а каждое из колес повернется на бесконечно малый угол δα вокруг мгновенного центра скоростей, совпадающего с точкой контакта колеса с опорной поверхностью. Вычислим сумму работ всех обозначенных на рис. 40 сил на этом перемещении:

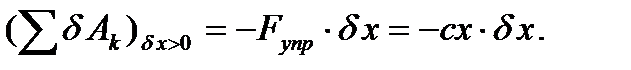
Отсюда найдем обобщенную силу, соответствующую обобщенной координате x

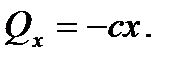
Придадим механической системе возможное перемещение, при котором обобщенная координата φ получает положительное приращение 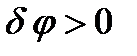, а обобщенная координата x останется неизменной (cм. рис. 41). При этом тележка останется неподвижной, а стержень ОА

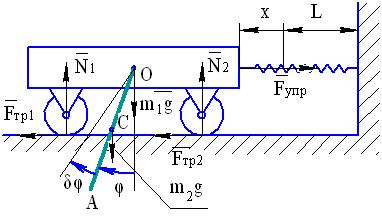
Рис. 41

повернется на угол δφ. Вычислим сумму работ всех сил на этом перемещении:

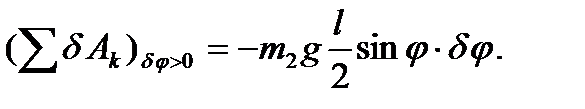
Отсюда найдем обобщенную силу, соответствующую обобщенной координате φ