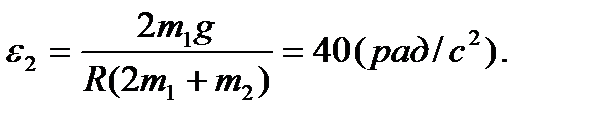Теорема об изменении кинетического момента

Кинетическим моментом (моментом количества движения) материальной точки относительно центра О называется векторный момент вектора 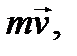вычисленный относительно центра О (см. рис. 20):

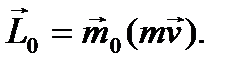
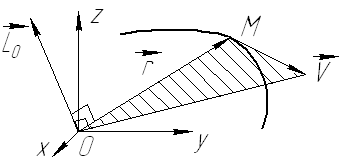
Рис. 20.

В соответствии с формулой для векторного момента кинетический момент точки можно представить в виде векторного произведения:

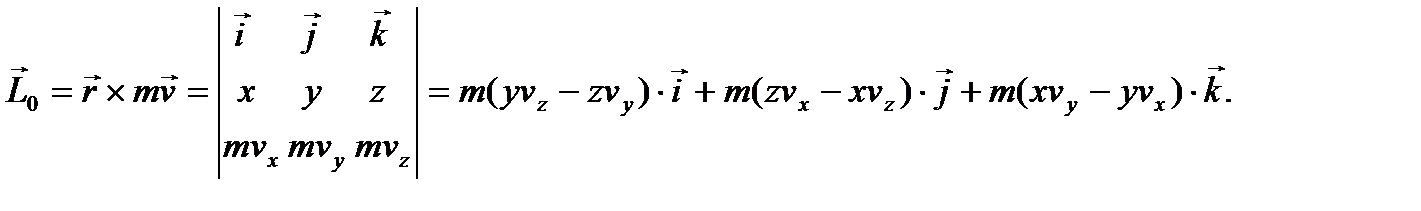(39)

Сомножители при ортах координатных осей в правой части формулы (39) являются проекциями кинетического момента точки на оси координат или кинетическими моментами точки относительно координатных осей.

Кинетическим моментом механической системы относительно центра О называется геометрическая сумма соответствующих кинетических моментов всех ее точек:

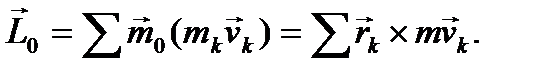(40)

Учитывая (39) для проекций вектора кинетического момента механической системы на оси координат можно записать

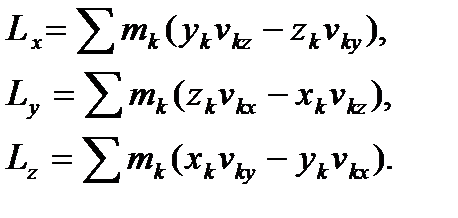(41)

Вычислим кинетический момент твердого тела, совершающего вращательное движение, относительно точки О, лежащей на оси вращения. Выберем оси координат с началом в точке О так, чтобы ось z была направлена вдоль оси вращения в сторону вектора угловой скорости 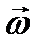(см. рис. 21).

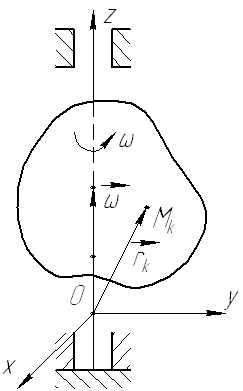
Рис. 21.

В этом случае, как известно из кинематики, вектор скорости k-й точки тела можно представить в виде векторного произведения

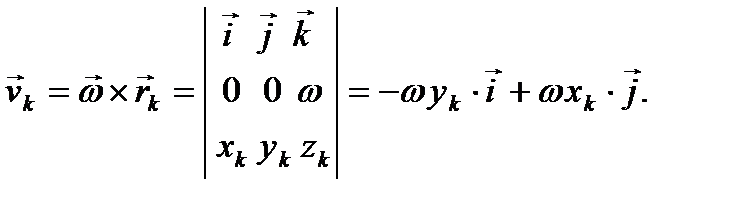
Отсюда следует, что проекции этого вектора на оси координат равны

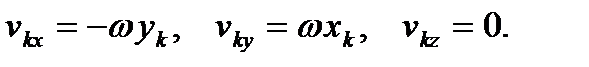
Подставляя эти значения в (41), получим следующие формулы для проекций вектора кинетического момента вращающегося тела:

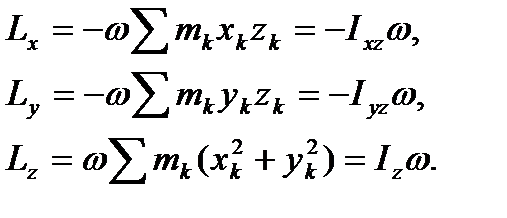(42)

Выведем теперь формулу, выражающую теорему об изменении кинетического момента. Запишем уравнения движения точек механической системы в виде:

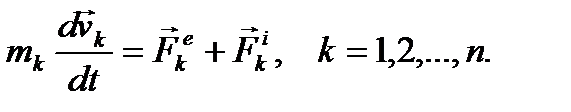
Умножим обе части каждого из этих равенств слева векторно на радиус-вектор 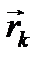соответствующей точки и почленно сложим получившиеся равенства:

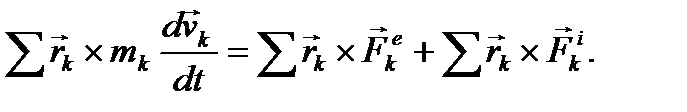(43)

Векторные произведения в правой части (43) выражают векторные моменты сил относительно точки О:

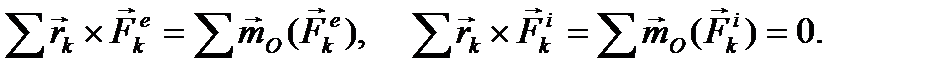
Вычислим теперь производную по времени от вектора кинетического момента механической системы:

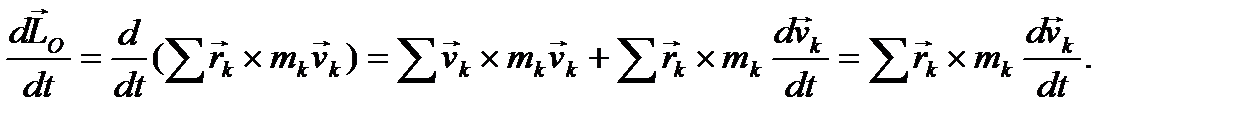
Здесь учтено, что 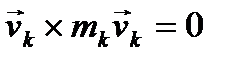как векторное произведение параллельных векторов. Получили, что левая часть (43) равна производной по времени от вектора кинетического момента. Окончательно из (43) получим

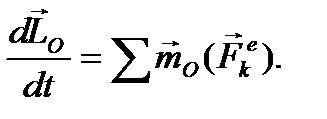(44)

Формула (44) выражает теорему об изменении кинетического момента механической системы:

Первая производная по времени от кинетического момента механической системы, вычисленного относительно центра О, равна геометрической сумме векторных моментов внешних сил, вычисленных относительно того же центра.

Замечания

1. Внутренние силы механической системы не могут изменить ее кинетического момента.

2. Эту теорему удобно использовать для изучения вращательного движения или для случая, когда главная часть движения является вращением. При этом векторное равенство (44) достаточно записать в проекциях на ось вращения:

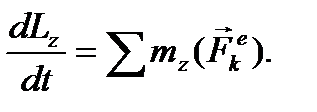(45)

Ось Oz удобно направлять вдоль оси вращения в сторону вектора угловой скорости. Тогда внешние силы, ускоряющие вращение, будут иметь положительные моменты относительно этой оси, а внешние силы, замедляющие вращение, будут иметь отрицательные моменты.

Следствия

1. Если сумма моментов внешних сил относительно некоторой оси равна нулю, 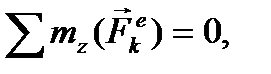то кинетический момент механической системы относительно этой оси при движении системы не изменяется:

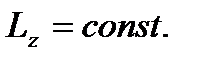
2. Если формулу (44) применить для изучения вращательного движения твердого тела, то согласно (42) 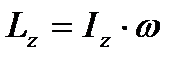и равенство (45) примет вид:

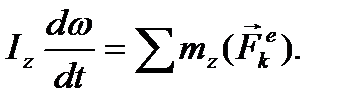(46)

Уравнение (46) называют дифференциальным уравнением вращательного движения твердого тела.

Пример 6

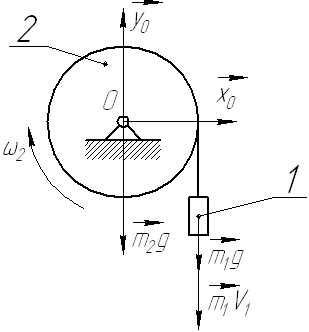
Рис. 22.

Груз 1 массой 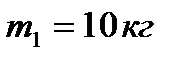подвешен на тросе, намотанном на барабан 2 радиуса R=0.2 м и массой 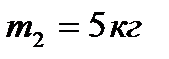(см. рис. 22). Движение начинается из состояния покоя под действием сил тяжести. Определить угловое ускорение барабана, считая его однородным цилиндром. Массой троса пренебречь.

Решение

Применим для решения задачи теорему об изменении кинетического момента рассматриваемой механической системы в проекциях на ось Oz, направленную вдоль оси вращения в сторону вектора угловой скорости:

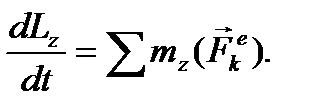
Обозначим на рисунке действующие на систему внешние силы: силы тяжести 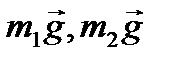и две составляющие реакции опорного шарнира 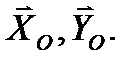Вычислим сумму моментов этих сил относительно оси Oz :

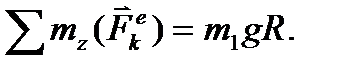(47)

Найдем далее кинетический момент механической системы относительно оси Oz :

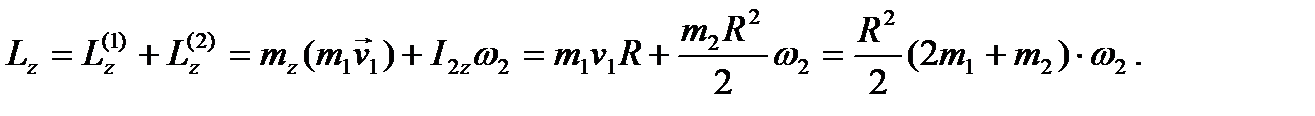
Здесь учтено, что 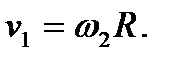Вычислим производную от 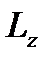по времени:

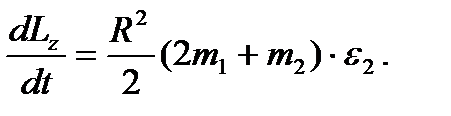(48)

Подставим теперь найденные выражения (47), (48) в формулу, выражающую теорему

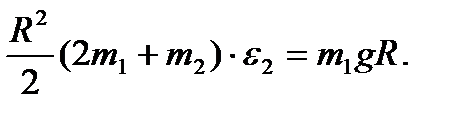
Отсюда найдем искомое угловое ускорение: