Инерционные характеристики механической системы

В данном параграфе рассмотрим инерционные характеристики механической системы. Заметим, что для изучения движения точки достаточно было ввести одну инерционную характеристику – массу точки. При рассмотрении движения механической системы потребуется большее количество инерционных характеристик. Дадим далее их определение.

Массоймеханической системы называется скалярная величина

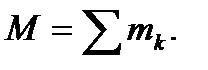(20)

Условимся в дальнейшем не указывать в формулах границы изменения индекса суммирования k, если суммирование производится по всем точкам механической системы.

Центром масс механической системы называется геометрическая точка C, радиус-вектор которой вычисляется по формуле

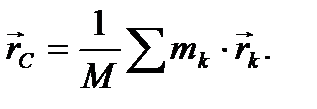(21)

Записав векторное равенство (21) в проекциях на оси декартовой системы координат получим формулы для координат центра масс

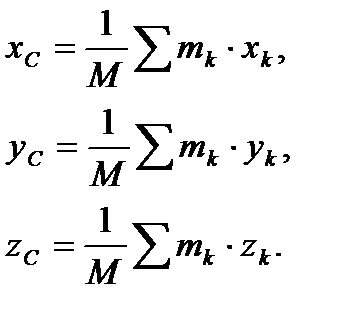
Осевым моментом инерции материальной точки называется скалярная величина, равная произведению массы точки на квадрат ее расстояния до оси.

Осевые моменты инерции точки относительно координатных осей могут быть вычислены по формулам (см. рис. 9):

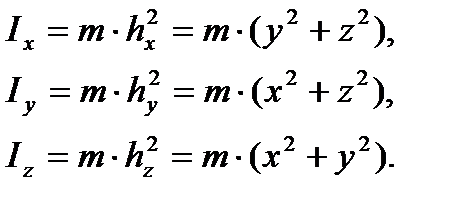
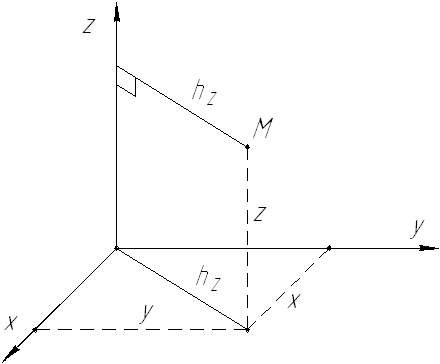
Рис. 9

Центробежным моментом инерции материальной точки относительно пары осей называется скалярная величина, равная произведению массы точки на две соответствующие осям координаты.

Формулы для вычисления центробежных моментов инерции имеют вид:

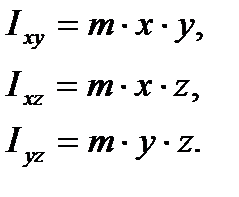
Моменты инерции для механической системы вычисляются путем суммирования соответствующих моментов инерции всех ее точек:

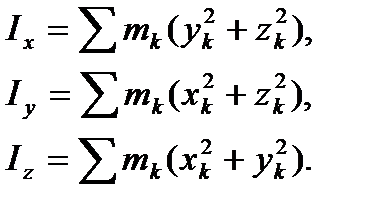(22)

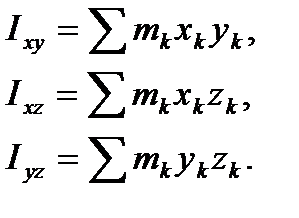(23)

Если масса в механической системе распределена непрерывно , то суммы в формулах (20)-(23) следует заменить на соответствующие интегралы. Например, пусть в качестве механической системы рассматривается твердое тело (см. рис. 10). Выберем элементарный объем тела dV массой dm=ρdV, где ρ – плотность. Тогда, например, формула (20) для массы тела запишется в виде

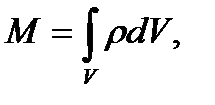
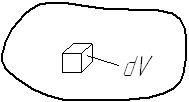
Рис. 10

а одна из формул (22) для осевого момента инерции относительно оси x примет вид

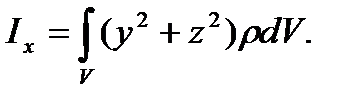
Радиусом инерции тела относительно оси называется величина, связанная с осевым моментом инерции по формулам

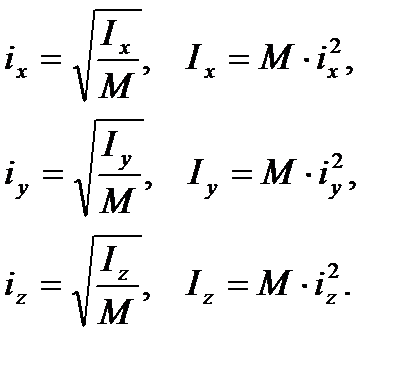(24)

Радиус инерции находится экспериментально для неоднородных тел или тел неправильной формы и используется для нахождения осевого момента инерции по формулам (24). Для однородных тел правильной формы осевые моменты инерции обычно находятся по аналитическим формулам, получающимся в результате вычисления соответствующих интегралов.

Далее кратко поясним физический смысл введенных моментов инерции.

Осевой момент инерции является мерой инертности механической системы при ее вращательном движении вокруг соответствующей оси.

Центробежные моменты инерции характеризуют асимметрию в распределении массы механической системы по отношению к координатным осям. Например, если ось x является осью материальной симметрии механической системы, то

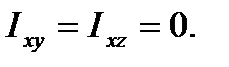
Если плоскость xoy является плоскостью материальной симметрии механической системы, то

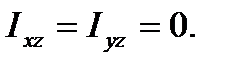
Теорема Штейнера

Момент инерции механической системы относительно какой-либо оси равен моменту инерции относительно параллельной оси, проходящей через центр масс, плюс произведение массы системы на квадрат расстояния между этими осями.

Доказательство

Выберем две системы координат с взаимно параллельными осями Oxyz и 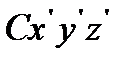, одна из которых имеет начало в центре масс С механической системы (см. рис. 11).

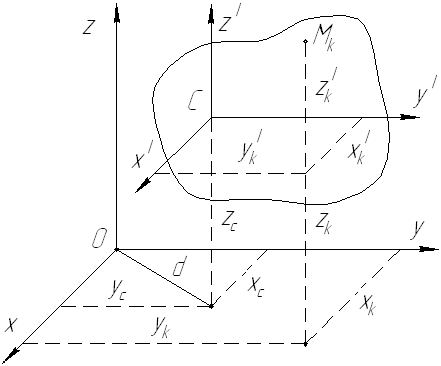
Рис. 11

В соответствии с (22) для осевых моментов инерции относительно осей z и 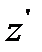имеем:

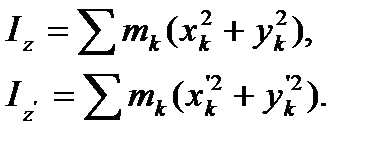
Очевидно (см. рис. 11), что координаты k-й точки в выбранных координатных осях связаны соотношениями:

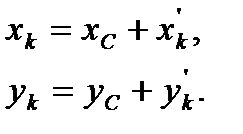
Подставим эти значения координат в выражение для момента инерции :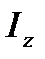

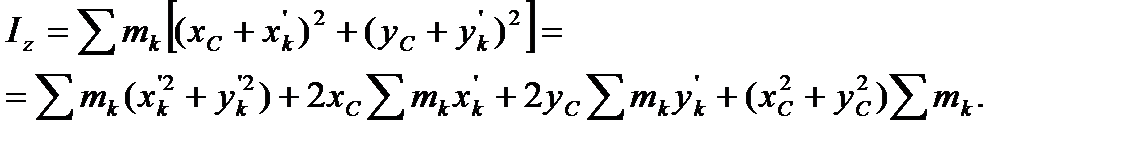
В этом выражении 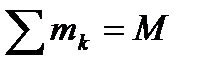- масса системы, 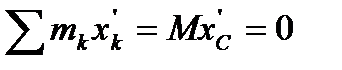и 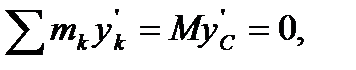так как 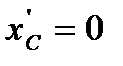и 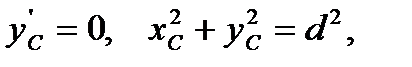где d – расстояние между осями Oz и 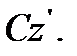Окончательно для момента инерции 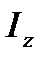получим формулу, выражающую доказываемую теорему:

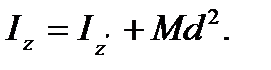(25)

Из (25) следует, что для совокупности параллельных осей момент инерции является наименьшим относительно оси, проходящей через центр масс.