Алгоритм локального улучшения

1. Выбрать начальный цикл и вычислить его длину

2. Найти наилучшего соседа для цикла

3. Если то положить и вернуться на 2, иначе STOP, – локальный минимум.

Теорема 5.3. Пусть 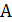– алгоритм локального улучшения и окрестность 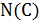имеет полиномиальную мощность. Если существует такая положительная константа что для любого примера 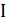задачи коммивояжера справедливо неравенство 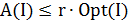, то классы P и NP совпадают.

Доказательство. (Аналогично предыдущему) Предположим, что такая константа существует. Рассмотрим задачу о гамильтоновом цикле и получим точный полиномиальный алгоритм ее решения. Снова по графу 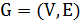построим матрицу:

Выбираем произвольный начальный цикл Его длина в худшем случае равна . На каждом шаге локального улучшения часть тяжелых ребер заменяется легкими ребрами. Значит, число итераций не превышает 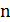. Каждая итерация имеет полиномиальную трудоемкость, так как число соседних решений полиномиально. Следовательно, алгоритм 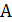является полиномиальным для заданного класса примеров и, как следует из доказательства предыдущей теоремы, 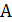– точный алгоритм. Значит, P = NP. ∎

Конструктивные алгоритмы

Конструктивными алгоритмами принято называть такие алгоритмы, которые постепенно, шаг за шагом, строят допустимое решение задачи, например, добавляя одно ребро за другим. Рассмотрим один из конструктивных алгоритмов для задачи коммивояжера, известный под названием «Иди в ближайший из непройденных городов». Далее будем предполагать, что матрица 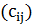удовлетворяет неравенству треугольника.

Алгоритм

1. Выбираем произвольный город, скажем, , и помечаем его.

2. Цикл

Находим ближайший город к из непомеченных городов, обозначаем его и помечаем город .

Теорема 5.4. Для любого найдется такой пример 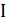задачи коммивояжера, что даже при выполнении неравенства треугольника справедливо неравенство .

C1

C2

C3

C4

C5

C6

C7

C8

C9

C10

C11

C12

C13

C14

C15

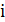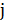Рассмотрим пример задачи коммивояжера, в котором города расположены на окружности на одинаковом расстоянии друг от друга. Длина окружности здесь является оптимальным значением, но алгоритм может сильно ошибаться. На рис. 5.2 показан пример для . Величина определяется как длина кратчайшего пути между и , получаемого с использованием ребер, изображенных на рисунке. Эти расстояния удовлетворяют неравенству треугольника. Длина окружности дает оптимальный маршрут 15, алгоритм дает маршрут длины 27.

Рисунок-5.2. Результат работы алгоритма

Рассмотрим теперь алгоритм, который имеет гарантированную точность . Он основан на следующей идее [17]. Для полного взвешенного графа задачи коммивояжера построим, например, алгоритмом Краскала остовное дерево минимального веса. Заметим, что для любого примера 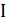, т. к. удаление ребра из оптимального решения задачи коммивояжера дает остовное дерево. Заменим каждое ребро на два ребра. Получим эйлеров граф, каждая вершина которого имеет четную степень. Построим эйлеров цикл (рис. 5.3).

Рисунок-5.3. Двойной обход остовного дерева

Перестроим его так, чтобы получился гамильтонов цикл. Начиная с произвольной вершины, двигаемся вдоль эйлерова цикла и помечаем вершины. Если очередная вершина уже помечена, то пропускаем ее и двигаемся дальше, пока не найдем непомеченную вершину или не вернемся в первую вершину. Цепочку дуг для помеченных вершин заменяем прямой дугой в непомеченную или первую вершину (рис. 5.4). Обозначим этот алгоритм .

Рисунок-5.4. Перестройка остовного дерева

Теорема 5.5. Для любого примера 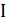задачи коммивояжера с симметричной матрицей 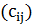, удовлетворяющей неравенству треугольника, алгоритм A_ST получает гамильтонов цикл не более чем в два раза длиннее оптимального, то есть

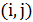Доказательство. Для двойного обхода остовного дерева имеем Пусть новое ребро , не содержащееся в двойном обходе, заменяет цепочку ребер . Из неравенства треугольника следует, что . Следовательно,

Теорема 5.6. Оценка точности является неулучшаемой для алгоритма .

Доказательство. Приведем семейство исходных данных задачи коммивояжера, на котором оценка 2 достигается асимптотически. Рассмотрим следующий пример на евклидовой плоскости с вершинами (рис. 5.5).

Рисунок-5.5. Пример на евклидовой плоскости

Для этого примера минимальное остовное дерево имеет вид (рис. 5.6.):

Рисунок-5.6. Минимальное остовное дерево

Длина остовного дерева . Алгоритм перестройки двойного обхода получит решение (рис. 4.7):

Рисунок-5.7. Результат алгоритма

Длина этого гамильтонова цикла (рис. 4.8). Оптимальное решение задачи .

Рисунок-5.8. Оптимальное решение

Таким образом, при и получаем . ∎

Теоремы 4.5 и 4.6 говорят не только о точности алгоритма в худшем случае. Они утверждают также, что оценка справедлива для любого эйлерова цикла, который будет перестраиваться в гамильтонов цикл. Но эйлеровых циклов может быть экспоненциально много. Выбирая из всех вариантов наилучший, можно существенно понизить ошибку. В. Дейнеко и А. Тискин [18] нашли точный полиномиальный алгоритм для выбора наилучшего эйлерова цикла. Оценка точности в худшем случае не изменилась, но поведение алгоритма в среднем показывает, что отклонение от нижней оценки оптимума не превышает 10 %. На сегодняшний день это один из лучших полиномиальных алгоритмов с точки зрения средней погрешности.

В заключение этого раздела приведем еще один полиномиальный алгоритм, предложенный независимо Н. Кристофидесом и А. Сердюковым. Эта улучшенная версия предыдущего алгоритма имеет оценку точности 3/2. Как и раньше, сначала строится остовное дерево минимального веса, затем к нему добавляются ребра так, чтобы получился эйлеров граф, а потом строится эйлеров цикл, который перестраивается в гамильтонов цикл. Новшество состоит в добавлении ребер для получения эйлерова графа. Вместо дублирования ребер остова в дереве выделяется множество вершин нечетной степени (рис. 5.9).

Рисунок-5.9. Построение множества

Их число четно, , так как сумма всех степеней вершин графа должна быть четной. На множестве находится совершенное паросочетание минимального веса: 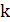ребер, имеющие минимальный суммарный вес и покрывающие все вершины. Эта задача полиномиально разрешима [20]. Более того, вес такого паросочетания не превосходит половины длины любого гамильтонова цикла. Действительно, гамильтонов цикл в исходном графе легко переделать в гамильтонов цикл для подграфа на вершинах из . Этого можно добиться, исключив вершины, не принадлежащие . В силу неравенства треугольника получим гамильтонов цикл не большей длины, чем исходный цикл. Он задает на множестве два паросочетания. Они получаются, если брать ребра через одно. Наименьший из весов этих паросочетаний не превосходит половины длины гамильтонова цикла. Добавим это паросочетание к остовному дереву (рис. 5.10).

Рисунок-5.10. Остовное дерево вместе с паросочетанием

Получим эйлеров граф. Его вес не превосходит 3/2 длины минимального гамильтонова цикла. Строим эйлеров цикл (рис. 5.11).

Рисунок-5.11. Эйлеров цикл

Перестраиваем эйлеров цикл в гамильтонов цикл описанным выше способом (рис. 5.12). Можно показать, что эту оценку нельзя улучшить, т. е. существуют примеры, на которых этот алгоритм действительно ошибается в 3/2 раза.

Рисунок-5.12. Гамильтонов цикл

Заметим, что новый подход снова порождает эйлеров граф, в котором может оказаться экспоненциально много эйлеровых циклов. Выбирая наилучший из них, можно существенно понизить погрешность получаемых приближенных решений. К сожалению, выбор наилучшего эйлерова цикла в данном случае оказывается NP-трудной задачей. Тем не менее, реализация этой идеи, пусть даже в виде приближенного решения, приводит, как и в предшествующем случае, к решениям с малой погрешностью.

Нижние оценки

Получение нижних оценок оптимума является важной задачей. Во-первых, они позволяют оценить погрешность конструктивных алгоритмов и вообще любых приближенных алгоритмов. Во-вторых, эти оценки используются в точных методах, например, методе ветвей и границ [16, 20]. Их качество часто оказывается критическим фактором при получении глобального оптимума. Ниже будут представлены четыре способа построения нижних оценок, каждый из которых имеет свои сильные и слабые стороны.

Примитивная нижняя оценка

Пусть величины задают минимальную плату за выезд из города. Так как коммивояжер должен выехать из каждого города, то является, очевидно, нижней оценкой оптимума. Рассмотрим теперь матрицу и для каждого города посчитаем минимальную плату за въезд: Тогда величина будет также нижней оценкой.

Теорема 5.7. Величина является нижней оценкой оптимума.

Доказательство. Оптимальные решения для матриц 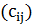и связаны соотношением .

Положим Тогда

∎

Основным достоинством этой нижней оценки является ее простота и наглядность. Ее вычисление требует 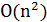операций, то есть линейной трудоемкости от числа элементов матрицы расстояний.