Некоторые задачи синтеза сетей, использующие деревья Штейнера

Задачи построения деревьев Штейнера, обладающих теми или иными свойствами, возникают при синтезе сетей передачи данных, при проектировании коммуникаций, дорог, трубопроводов, при трассировке сверхбольших интегральных схем (СБИС) и т. п.

Рассмотрим для примера следующую задачу построения МДШ с ограничениями на длины путей из заданной вершины (корень или источник сигнала), которая возникает в связи с трассировкой СБИС. В [10] задача поставлена следующим образом.

Задан взвешенный граф 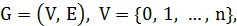где выделенную вершину 0 назовем корнем. Для каждого терминала 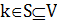задана максимально допустимая длина пути из корня 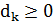. Каждому ребру графа (i, j) Î E приписаны целочисленные «вес» 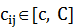и «длина»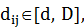 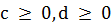. Требуется решить задачу

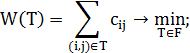	(4.1)
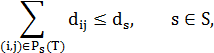	(4.2)

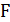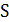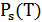где – множество деревьев Штейнера, связывающих вершины множества , а – путь из корня в вершину 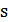в дереве .

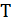Задача (4.1) – (4.2) остается NP-трудной даже в случае .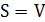

В [10] предложен следующий эвристический алгоритм для решения задачи (4.1) – (4.2).

Сначала строящееся дерево состоит из одного корня 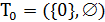. На каждой итерации алгоритма 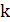к дереву, построенному на предыдущих шагах 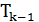, добавляются одна вершина 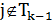и одно ребро :

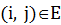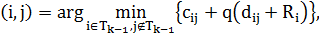
где 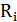– длина пути 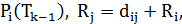параметр 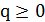, в результате чего получаем дерево .

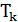Варьирование значений параметра 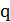позволяет контролировать «качество» решения. В частности, доказано, что в случае целочисленных весов и длин ребер приведенный алгоритм строит дерево кратчайших путей 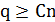при . При 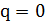алгоритм, очевидно, строит некое дерево Штейнера без учета ограничений на длины путей. Меняя значения параметра, можно получать разные деревья и запомнить в качестве приближенного решения лучшее допустимое дерево. Показано, что для построения разных деревьев достаточно запустить алгоритм с конечным числом значений 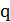, что приводит к полиномиальной трудоемкости всего алгоритма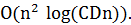

Приведенный алгоритм не имеет гарантированной оценки точности, и для его анализа проведен численный эксперимент, показавший высокую эффективность.

Обратимся к следующему примеру. Одним из этапов проектирования сверхбольших интегральных схем (после размещения элементов на СБИС) является трассировка соединений или маршрутизация. Этот этап разбивается на глобальную и детальную маршрутизацию.

Глобальная трассировка является одним из важнейших этапов проектирования СБИС, на котором для каждой цепи определяется множество используемых областей маршрутизации в условиях ограничений на трассировочные ресурсы и время прохождения сигнала. В литературе встречается несколько формулировок задачи глобальной трассировки (ЗГТ) с различными критериями и ограничениями. Основной целью глобальной трассировки является маршрутизация всех цепей СБИС без нарушения ограничений. При этом даже простейшая постановка, в которой требуется осуществить маршрутизацию двухтерминальных цепей в условиях ограниченности трассировочных ресурсов (без учета временных задержек), является NP-трудной задачей.

Для решения ЗГТ исследователями предложены различные подходы, в которых трассировка, как правило, осуществляется лишь на двух слоях. В основе этих подходов лежат алгоритмы последовательной маршрутизации, алгоритмы трассировки с разрывом связей и поиском новых соединений, алгоритмы, основанные на решении задач о многопродуктовом потоке, иерархические методы, а также различные метаэвристики.

При проектировании современных СБИС на этапе глобальной маршрутизации, наряду с учетом трассировочных ресурсов, все большее внимание уделяется времени распространения сигнала. При этом плотность соединений и временнáя задержка являются, как правило, конкурирующими критериями, и в литературе практически отсутствуют публикации, в которых эти критерии рассматриваются совместно.

Логическая схема СБИС может быть представлена ациклическим графом с несколькими основными входами и основными выходами. Она включает в себя разнотипные элементы, связанные частично упорядоченными цепями. Каждый элемент схемы реализует определенную булеву функцию и имеет несколько входов и один выход, которые наряду с основными входами и выходами называются терминалами. Цепь задается одним терминалом-источником и несколькими терминалами – получателями сигнала. Например, на рис. 4.4 цепь, выделенная жирными линиями, имеет один источник – выход элемента 5 – и четыре терминала, которые являются входами элементов 7, 8, 9 и 11.

Рисунок- 4.4. Пример логической сети

Для каждого основного входа схемы задано время поступления сигнала извне (AT – arrival time), а для каждого основного выхода – наиболее позднее допустимое время получения сигнала, которое назовем директивным (RT – required time).

Область размещения элементов и трассировки состоит из одинаковых прямоугольников, расположенных друг над другом, которые называются слоями. Размещение элементов интегральной схемы осуществляется до трассировки, поэтому координаты всех терминалов предполагаются известными.

Терминалы соседних слоев связываются межслойными соединениями (за межслойным соединением в англоязычной литературе закрепился термин «via»), которые будем считать параллельными оси 0z. Трассировка на каждом слое осуществляется либо параллельно оси 0x, либо параллельно оси 0y. При этом некоторые слои могут использоваться только для размещения элементов схемы.

На этапе глобальной маршрутизации все слои СБИС разбиваются на одинаковые глобальные ячейки, имеющие форму прямоугольников.

Рисунок-4.5. Пример построения глобального графа

В результате каждый терминал попадает в одну из таких ячеек. Затем строится следующий глобальный граф. Каждой глобальной ячейке ставится в соответствие глобальная вершина. Пара глобальных вершин соединяется глобальным ребром в следующих случаях (рис. 4.5):

– если они расположены на одном слое, и соответствующие им глобальные ячейки имеют общую сторону, которая перпендикулярна направлению маршрутизации на данном слое;

– если эти вершины расположены на соседних слоях, и их (x, y)-координаты совпадают.

Для соединения терминалов произвольной цепи используется дерево Штейнера в глобальном графе. Каждому глобальному ребру приписан трассировочный ресурс или пропускная способность – максимальное число вхождений этого ребра в совокупность деревьев Штейнера.

Итак, пусть задан глобальный граф 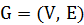с множеством вершин 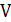и множеством ребер 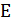. Каждому ребру 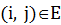приписана длина 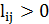, емкостное сопротивление (емкость) 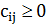, электрическое сопротивление (сопротивление) 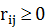и пропускная способность .

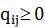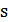Цепь (будем обозначать ее просто номером 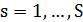) задана множеством терминалов 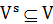. Для терминалов, являющихся основными входами СБИС, заданы времена поступления сигналов извне (ATs). Для каждого из основных выходов задано наиболее позднее допустимое время получения сигнала (RT). Терминал 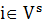обладает емкостью 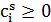, которая определяется типом элемента.У каждой цепи s имеется один источник 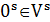, имеющий сопротивление .

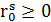Для аналитического вычисления времен прохождения сигнала в современных СБИС обычно используется модель Эльмора. Пусть задано дерево 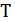с корнем в вершине 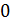. Обозначим через:

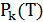– - путь из корня в вершину 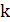в этом дереве ;

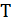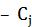– емкость поддерева 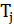с корнем в вершине 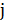, то есть

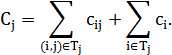
Тогда время прохождения сигнала по дуге 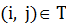вычисляется по формуле:

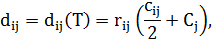	(4.3)

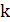а время прохождения сигнала из корня в произвольную вершину дерева 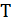вычисляется по формуле:

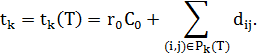(4.4)

Пусть временные задержки вычисляются по формулам Эльмора (4.3)–(4.4). В заданном n-вершинном дереве трудоемкость этих вычислений ограничена величиной .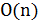

В ЗГТ требуется связать вершины каждого множества 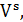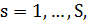деревом Штейнера таким образом, чтобы каждое ребро глобального графа 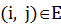вошло не более чем в 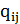различных деревьев, и время прихода сигнала в каждый основной выход СБИС не превышало директивное (RT).

На практике допустимая трассировка может не существовать, либо ее сложно найти из-за большой размерности задачи и ее NP-трудности. Поэтому рассматривается проблема построения трассировки, близкой к допустимой, и в дальнейшем именно такую задачу мы будем называть задачей глобальной трассировки. Другими словами, ЗГТ состоит в отыскании трассировки, являющейся компромиссом между превышением трассировочных ресурсов и временем прохождения сигнала.

Для решения ЗГТ предлагается следующая итеративная процедура. Сначала осуществляется сортировка цепей, основанная на одном из эмпирических критериев, в качестве которых могут использоваться количество терминалов цепи, периметр минимального прямоугольника, содержащего все терминалы цепи, и другие. Затем для каждой цепи 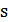из упорядоченного списка, с учетом временных задержек и остаточных пропускных способностей ребер глобального графа, строится множество 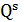деревьев-кандидатов. Далее выбирается по одному дереву из каждого множества 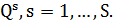Для этого рассматривается проблема минимизации суммы штрафов за превышение трассировочных ресурсов, которая сформулирована в форме задачи квадратичного целочисленного программирования. Адаптированный градиентный алгоритм находит решение непрерывной релаксации последней задачи, и затем с помощью различных эвристик строятся целочисленные решения, лучшее из которых выбирается в качестве приближенного решения ЗГТ.

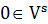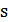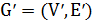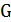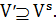Для построения деревьев с учетом времени прохождения сигнала предложен алгоритм МАД. Рассмотрим произвольную цепь s с источником сигнала в вершине . Алгоритм МАД строит дерево Штейнера для цепи в некотором связном подграфе графа , где Из 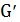удаляются ребра, пропускная способность которых меньше некоторого целого 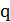, являющегося параметром алгоритма. Для каждого оставшегося ребра 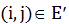по формуле (4.3) вычисляется задержка 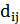, для чего может использоваться дерево, построенное на предыдущей итерации (вначале это дерево не содержит ребер). Различные способы подсчета 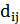обсуждаются ниже.

Описанный алгоритм является модификацией алгоритма Дейкстры, но не гарантирует построение дерева с минимальными задержками в силу специфики модели Эльмора. Заметим, что построение дерева с минимальными временами прохождения сигнала из корня в терминалы является NP-трудной проблемой, т. к. 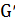частный случай, когда сопротивления всех ребер нулевые, есть задача Штейнера на графах.Топология построенного дерева зависит от подграфа , параметра 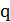и величин 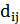. В качестве 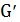можно использовать весь граф 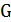, граф Ханана, минимальную решетку, содержащую множество терминалов цепи, либо другие подграфы глобального графа. Для построения различных деревьев с учетом задержек Эльмора предлагается применять алгоритм МАД итеративно, используя ранее построенные деревья для вычисления 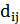. Как видно из формулы (4.3), величина 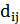зависит от емкости 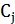поддерева 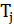. Поскольку емкость поддерева 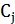в процессе построения дерева неизвестна, то для вычисления 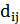можно использовать значения этой величины в построенных ранее деревьях. Например, 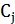может быть емкостью поддерева 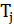, построенного на предыдущей итерации, или средним арифметическим емкостей поддеревьев 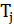во всех ранее построенных деревьях.Разнообразия деревьев, строящихся алгоритмом МАД, можно добиться изменением значений параметра 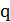. Кроме этого, можно использовать деревья, построенные другими алгоритмами. Например, если сопротивление и емкость соединения пропорциональны длине соединения, можно строить в качестве деревьев-кандидатов минимальные деревья Штейнера, а также деревья, содержащие кратчайшие пути из корня в терминалы. Так как задача построения минимального дерева Штейнера принадлежит классу NP-трудных проблем, то следует применять различные приближенные алгоритмы, которые будут строить разные деревья. Это расширит множества деревьев-кандидатов, что может позволить найти лучшее решение с учетом трассировочных ресурсов глобального графа.Пусть для каждой цепи 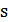найдено множество деревьев-кандидатов 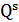. Если для некоторого 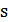множество 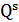состоит из единственного дерева, то оно включается в решение, после чего пересчитываются пропускные способности глобальных ребер, а цепь 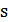исключается из списка. Рассмотрим задачу оптимального распределения трассировочных ресурсов, то есть задачу выбора деревьев из множеств 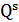, таких, что 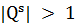. Для краткости записи в дальнейшем индекс 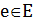используется для ребер графа 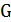, а индекс 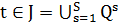- для деревьев. 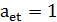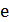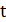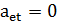Положим , если ребро принадлежит дереву , и в противном случае. Переменная 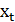принимает значение 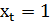, если дерево 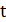выбрано, и 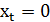в противном случае.

В принятых обозначениях рассмотрим задачу:

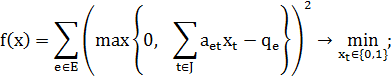	(4.5)
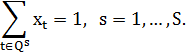	(4.6)

Целевая функция (3.5) равна сумме штрафов за превышение трассировочных ресурсов 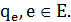Трассировке без превышения пропускных способностей глобальных ребер соответствует нулевое значение целевой функции.

Заменяя условие целочисленности переменных условием их неотрицательности, получаем непрерывную релаксацию задачи (4.5)–(4.6). Гладкость и выпуклость целевой функции позволяет применить для решения последней задачи градиентный алгоритм. Предложен градиентный алгоритм, в котором трудоемкость каждой итерации равна 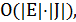а общее число итераций не превосходит 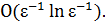В описанном методе на каждой итерации мы не стремимся найти направление наискорейшего спуска, что увеличило бы трудоемкость алгоритма, а выбираем направление спуска из текущей точки в целую точку.

Выбор одного дерева 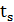из каждого множества 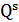дает множество деревьев Штейнера, которое является приближенным решением задачи (4.5)–(4.6). Это множество деревьев зависит от текущей точки и поэтому может меняться от итерации к итерации. В процессе спуска будем хранить лучшее (например, в смысле критерия (4.5), или плотности соединений) из найденных решений.

Приведем еще один пример построения сигнального дерева в вычислительной системе. Сигнальная сеть отвечает за синхронизацию работы вычислительной системы. Сигналы-команды генерируются вне системы и подаются в нее через вход (корень). Каждый функциональный элемент связан с корнем посредством сигнальной сети. Элемент выполняет серии логических операций (функций) и ждет сигнала для передачи результатов другим элементам, пока не начнется следующий цикл вычислений. Таким образом, происходит контроль информационных потоков внутри вычислительной системы. Временнóй перекос (или clock skew в англоязычной литературе) – это максимальная разница между моментами получения сигналов различными компонентами системы. Увеличение временного перекоса в вычислительных системах ведет к уменьшению скорости вычислений. В современных системах, когда размеры элементов существенно меньше микрона, временной перекос является одним из основных факторов, определяющих функционирование системы. Временной перекос уменьшает тактовую частоту, так как период между двумя последовательными сигналами должен быть увеличен, чтобы все компоненты схемы успели получить сигнал. Считается, что для высокоскоростных схем временной перекос не должен превышать 5 % от максимального времени передачи сигнала.

Рассматриваемую проблему синхронизации получения сигналов-команд элементами вычислительной системы можно сформулировать следующим образом. Каждый терминал (элемент схемы) выполняет определенные операции. Все терминалы выполняют часть общей программы и должны работать согласованно. Требование получения сигналов всеми терминалами одновременно можно удовлетворить, если построить дерево, в котором все пути из источника в терминалы имеют одинаковые задержки. Такое дерево назовем допустимым. Кроме того, среди допустимых деревьев следует выбрать дерево минимального веса, что позволит минимизировать занятое деревом пространство.

При этом маршрутизация ребер дерева производится на равномерной прямоугольной плоской решетке (в частности, имеем, что степень каждой вершины в таком графе не превосходит четырех). Следовательно, не всегда возможно построение допустимого дерева.

С математической точки зрения проблема заключается в построении минимального прямоугольного дерева Штейнера, в котором расстояния (по дереву) из корня до каждого терминала равны радиусу графа-решетки. Известно, что такая задача является NP-трудной. Приближенный алгоритм решения задачи предложен, например, в [14].

Примеры и упражнения

Пример 4.1.Пусть требуется связать МДШ четыре точки расположенные на плоскости попарно симметрично относительно горизонтальной прямой (рис. 4.6).

120°

120°

Рисунок-4.6. Вершины степени 3 – точки Штейнера

Решение. Из свойств геометрического МДШ следует, что число точек Штейнера не превосходит 2, и инцидентные им ребра образуют угол в 120°. Проведем горизонтальную прямую на одинаковом расстоянии между левыми и правыми точками. Из каждой точки проведем прямую, пересекающуюся с горизонтальной прямой под углом 120°. Точки пересечения – точки Штейнера. МДШ построено, в него вошли 2 точки Штейнера (см. рис. 4.6).

Пример 4.2. Пусть вершины графа расположены в узлах единичной решетки на рис. 4.7. Требуется связать терминалы
2-приближенным деревом Штейнера с использованием прямоугольной метрики L₁.

Решение. Построим сначала решетку Ханана, проведя горизонтальные и вертикальные линии, проходящие через терминалы (рис. 4.7a). Найдем длины кратчайших путей между каждой парой терминалов и построим МОД (рис. 3.7b). На решетке представление построенного дерева не однозначно, но любое представление будет 2-приближенным решением задачи Штейнера. На рис. 3.7a представлено дерево, которое является МДШ.

Рисунок-4.7.Решетка Ханана (a) и минимальное остовное дерево (b)

Пример 4.3. Для иллюстрации работы метода

решения ЗГТ приведем пример. Пусть имеется 11 сетей, 3 слоя и решетка 5´2. Все элементы СБИС расположены на первом (нижнем) слое, межслойные соединения имеют высокую пропускную способность, нулевую емкость и сопротивление 0.00937. Второй слой используется для осуществления «вертикальных» соединений (то есть параллельных оси 0y), линия связи (соответствующее ребро глобального графа) имеет пропускную способность 16, удельную емкость 0.470431, удельное сопротивление 0.016209. Межслойные соединения между слоями 2 и 3 имеют высокую пропускную способность, нулевую емкость и сопротивление 0.00781. Третий уровень используется для соединений, параллельных оси 0x, имеет пропускную способность – 12, удельную емкость 0.456122 и удельное сопротивление 0.010763.

На рис. 4.8 приведен результат работы метода, который построил трассировку с плотностью (максимальным количеством соединений на одном ребре графа) 5. Время прихода сигнала (AT) в основной выход 12 – это 34 ps (пикосекунды), и AT в основной выход 13 - 36 ps. На рис. 3.9 приведена проекция деревьев на плоскость (x, y).

Рисунок-4.8. Пример маршрутизации в 3-слойном глобальном графе

Рисунок-4.9. Проекции деревьев

Рисунок-4.10. 5-слойная маршрутизация (плотность равна 3)

Этот же пример был решен после добавления двух слоев (удельное сопротивление слоев 4 и 5 мы уменьшили в 10 раз по сравнению со слоями 2 и 3, удельная емкость и характеристики via оставили без изменения, как на слоях 2 и 3 соответственно). Алгоритм построил решение, показанное на рис. 4.10, с плотностью маршрутизации 3. Здесь мы не учитывали плотность via-соединений, т. к. пропускные способности таких ребер в примере не ограничены. Времена прихода сигнала в основные выходы схемы 12 и 13 соизмеримы с аналогичными временами для 3-слойной маршрутизации.

Упражнение 4.1. Построить МДШ в графе, изображенном на рис. 4.7a, для случая евклидовой метрики.

Упражнение 4.2. Построить МДШ в графе, изображенном на рис. 4.7a, в котором длины путей из левого нижнего терминала минимальны (для случая евклидовой метрики).

Упражнение 4.3. Построить МДШ в графе, изображенном на рис. 4.7a, в котором длины путей из левого нижнего терминала минимальны (для случая прямоугольной метрики).

ЗАДАЧА КОММИВОЯЖЕРА

В задаче коммивояжера задана матрица попарных расстояний между 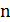городами. Требуется найти такой порядок посещения городов, чтобы пройденное расстояние было минимальным, каждый город посещался ровно один раз, и коммивояжер вернулся в тот город, с которого начал свой маршрут. Другими словами, во взвешенном полном неориентированном графе требуется найти гамильтонов цикл минимального веса. Если граф ориентированный и вес прямой дуги может не совпадать с весом обратной дуги, то требуется найти гамильтонов контур минимального веса.

Задача коммивояжера занимает особое место в комбинаторной оптимизации и исследовании операций. Исторически она была одной из тех задач, которые послужили толчком для развития этих направлений. Простота формулировки, конечность множества допустимых решений, наглядность и в тоже время колоссальные затраты на полный перебор до сих пор подталкивают математиков к разработке все новых и новых численных методов. Фактически, все свежие идеи сначала тестируются на этой задаче. С точки зрения приложений она не представляет интерес. Куда важнее ее обобщения для задач транспортировки грузов и логистики, когда несколько транспортных средств ограниченной грузоподъемности должны обслуживать клиентов, посещая их в заданные временные окна. В классической задаче коммивояжера все детали реальных приложений отсутствуют. Оставлена только комбинаторная суть, чисто математическая проблема, с которой не удается справиться уже полвека. Именно этой широко известной задаче посвящена данная глава.

Вычислительная сложность

Известно, что задача о гамильтоновости графа является NP-полной. В задаче коммивояжера требуется найти гамильтонов цикл минимальной длины. Это не задача распознавания. Она не лежит в классе NP, но она не проще проверки гамильтоновости графа. Действительно, если существует точный полиномиальный алгоритм для задачи коммивояжера, то можно легко построить точный полиномиальный алгоритм и для проверки гамильтоновости графа. Для этого достаточно по графу 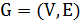, чью гамильтоновость мы исследуем, построить матрицу расстояний 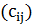задачи коммивояжера по следующему правилу: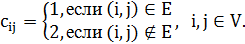

Если на решении задачи коммивояжера функционал равен 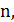то граф 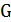является гамильтоновым. Обратное тоже верно. Задачи вне класса NP, которые не проще NP-полных задач, называют NP-трудными. Задача коммивояжера принадлежит этому классу. Фактически мы получили доказательство даже более сильного утверждения.

Теорема 5.1. Задача коммивояжера является NP-трудной, даже когда матрица 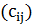является симметричной и состоит из 1 и 2.

Легко проверить, что неравенство треугольника 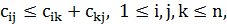в этом случае также выполняется. Говорят, что задача является NP-трудной в сильном смысле, если она остается NP-трудной даже при унарной кодировке исходных данных. При двоичной кодировке целое число 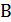требует 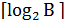ячеек памяти. При унарной кодировке требуется 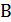ячеек памяти. Переход к унарной кодировке влечет рост требуемой памяти и, как следствие, рост длины записи исходных данных. Грубо говоря, задача является NP-трудной в сильном смысле, если она остается NP-трудной, когда все числа в исходных данных ограничены некоторой константой.
Из приведенного выше доказательства следует, что задача коммивояжера является NP-трудной в сильном смысле.

Полученное утверждение говорит о том, что точный полиномиальный алгоритм для задачи коммивояжера построить, скорее всего, не удастся. По-видимому, таких просто не существует. Следовательно, надо либо выйти за рамки полиномиальных алгоритмов, либо искать приближенные решения задачи. Следующая теорема говорит о том, что второй подход может оказаться не проще точного решения задачи. Пусть для примера 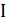задачи коммивояжера величина 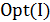задает длину кратчайшего гамильтонова цикла, а некоторый алгоритм 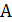на этом примере дает ответ .

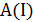Теорема 5.2. Если существует приближенный полиномиальный алгоритм 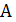и такая положительная константа 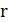, что для любого примера 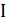задачи коммивояжера справедливо неравенство

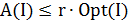, то классы P и NP совпадают.

Доказательство. Рассмотрим снова задачу о гамильтоновом цикле и построим матрицу 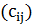по следующему правилу: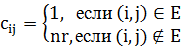

Применим приближенный алгоритм 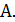Если 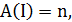то граф содержит гамильтонов цикл.

Предположим, что 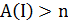. Тогда 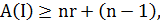так как путь коммивояжера проходит как минимум через одно «тяжелое» ребро. Но в этом случае граф не может иметь гамильтонов цикл, так как алгоритм ошибается не более чем в 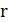раз. Следовательно, полиномиальный алгоритм 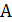дает правильный ответ для NP-полной задачи и P = NP. ∎

Из доказательства теоремы следует, что константу 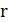можно заменить на любую, например, экспоненциально растущую функцию от 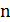. Повторяя рассуждения, получаем, что относительная точность полиномиальных алгоритмов в худшем случае не может быть ограничена, в частности, величиной 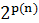, где 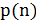– произвольный полином от размерности задачи, если P ≠ NP.

Заметим, что, в отличие от доказательства теоремы 5.1, новая конструкция уже не гарантирует выполнение неравенства треугольника. Это наводит на мысль, что при дополнительных ограничениях на матрицу 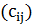можно получить полиномиальные алгоритмы с гарантированной точностью. Это действительно так, и ниже будут представлены такие алгоритмы для матриц, удовлетворяющих неравенству треугольника. Подробный обзор таких алгоритмов можно найти, например, в [14].

Рассмотрим теперь другой класс алгоритмов – итерационные алгоритмы локального улучшения. Каждая итерация будет иметь полиномиальную трудоемкость, но число итераций может оказаться в худшем случае экспоненциальной величиной. Пусть 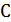– гамильтонов цикл, а 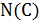– окрестность цикла 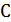, то есть все циклы, которые можно получить из цикла 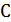некоторой локальной перестройкой. Например, 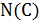– окрестность 2-замена: выбираем в 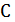два несмежных ребра и меняем их на два других, чтобы снова получить гамильтонов цикл (рис. 5.1).

a

b

c

d

a

b

c

d

Рис. 5.1. Окрестность 2-замена

Мощность такой окрестности – 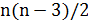. Аналогично можно получить окрестность 3-замена, 4-замена и т. д.