Постановки задачи Штейнера и ее сложность
Пусть задан неориентированный простой взвешенный граф 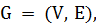 в котором множество вершин является объединением двух множеств
в котором множество вершин является объединением двух множеств 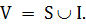 Вершины множества
Вершины множества 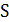 будем называть терминалами, а вершины из множества
будем называть терминалами, а вершины из множества 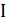 – промежуточными вершинами. Каждому ребру
– промежуточными вершинами. Каждому ребру 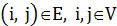 , приписана «длина»
, приписана «длина» 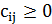 . Требуется связать все вершины множества
. Требуется связать все вершины множества 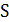 деревом минимальной длины, которое называется минимальным деревом Штейнера (МДШ). При этом в искомое дерево могут войти промежуточные вершины из множества
деревом минимальной длины, которое называется минимальным деревом Штейнера (МДШ). При этом в искомое дерево могут войти промежуточные вершины из множества 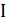 .
.
Рисунок-4.2. Пример дерева Штейнера на графе
На рис. 4.2 пунктирными линиями изображены ребра графа 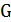 , которые соединяют терминалы – закрашенные вершины и промежуточные (не закрашенные) вершины. Сплошными линиями показано дерево Штейнера, в которое вошли три промежуточные вершины.
, которые соединяют терминалы – закрашенные вершины и промежуточные (не закрашенные) вершины. Сплошными линиями показано дерево Штейнера, в которое вошли три промежуточные вершины.
Для МДШ на плоскости с евклидовой метрикой справедливы следующие свойства.
Свойство 4.1. Точка Штейнера имеет степень 3.
Свойство 4.2. Если вершина 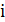 имеет степень 3 в МДШ, то угол между любыми двумя ребрами, инцидентными
имеет степень 3 в МДШ, то угол между любыми двумя ребрами, инцидентными 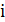 , равен 120°.
, равен 120°.
Свойство 4.3. Число точек Штейнера в МДШ равно 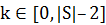 .
.
Известно, что задача Штейнера на графах (а также геометрическая задача Штейнера) NP-трудна в сильном смысле [4], поэтому на практике используются различные приближенные алгоритмы для построения МДШ.
Приближенные алгоритмы
Очевидно, МОД является приближенным решением задачи Штейнера. При этом для метрического случая, когда точки (вершины) расположены на плоскости, отношение 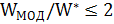 ,
,
где 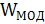 – вес минимального остовного дерева, а
– вес минимального остовного дерева, а 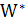 – минимальная длина дерева Штейнера. Алгоритм Прима (Краскала) строит 2-приближенное решение задачи Штейнера с полиномиальной трудоемкостью.
– минимальная длина дерева Штейнера. Алгоритм Прима (Краскала) строит 2-приближенное решение задачи Штейнера с полиномиальной трудоемкостью.
Известен более сильный результат: 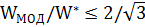 , для метрической задачи с евклидовой метрикой. Предложено также несколько алгоритмов, которые строят 2-приближенное решение задачи Штейнера на произвольных графах. Например, достаточно найти кратчайшие пути между каждой парой вершин графа, перейти к вспомогательному графу без промежуточных вершин с длинами ребер, равными длинам кратчайших путей, и построить МОД. Это и будет 2-приближенное решение для исходной задачи Штейнера.
, для метрической задачи с евклидовой метрикой. Предложено также несколько алгоритмов, которые строят 2-приближенное решение задачи Штейнера на произвольных графах. Например, достаточно найти кратчайшие пути между каждой парой вершин графа, перейти к вспомогательному графу без промежуточных вершин с длинами ребер, равными длинам кратчайших путей, и построить МОД. Это и будет 2-приближенное решение для исходной задачи Штейнера.
Опубликован ряд работ, в которых предложены алгоритмы с меньшей оценкой точности, например, алгоритм строящий 1.55-приближенное решение для точек, расположенных на плоскости, расстояния между которыми задаются прямоугольной (манхэттеновской) метрикой 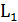 [9]. В этом случае дерево Штейнера состоит из множества вертикальных и горизонтальных отрезков, соединяющих терминалы и промежуточные точки. Однозначно определяется минимальный прямоугольник, в котором находятся все терминалы, и его стороны параллельны осям (прямоугольник ABCD на рис. 3.3). Очевидно, все ребра МДШ не выходят за пределы этого прямоугольника. В 1966 г. Ханан показал [10], что существует МДШ, в которое входят только узлы решетки, полученной от пересечения горизонтальных и вертикальных прямых, проходящих через терминалы, – решетка Ханана (рис. 3.3).
[9]. В этом случае дерево Штейнера состоит из множества вертикальных и горизонтальных отрезков, соединяющих терминалы и промежуточные точки. Однозначно определяется минимальный прямоугольник, в котором находятся все терминалы, и его стороны параллельны осям (прямоугольник ABCD на рис. 3.3). Очевидно, все ребра МДШ не выходят за пределы этого прямоугольника. В 1966 г. Ханан показал [10], что существует МДШ, в которое входят только узлы решетки, полученной от пересечения горизонтальных и вертикальных прямых, проходящих через терминалы, – решетка Ханана (рис. 3.3).
Рисунок-4.3. Минимальное дерево Штейнера (жирные линии) на решетке Ханана
В 1976 г. Хванг [11] показал, что МОД является 3/2-приближен-ным решением. В 1992 г. Зеликовский [12] разработал алгоритм построения прямоугольного дерева Штейнера с оценкой точности 11/8, первый эвристический алгоритм, который строит решение лучше МОД.
