Двойственность в ЛП. Понятие двойственности
С каждой задачей ЛП связана двойственная (т.е. обратная) задача. Первоначальная задача является исходной (или прямой). Связь исходной и двойственной задач состоит в том, что коэффициенты сj линейной формы L(х) исходной задач и является свободными членами системы ограничений двойственной задачи. Свободные члены bi системы ограничений исходной задачи служат коэффициентами функции цели двойственной задачи. Матрицами коэффициентов системы ограничений двойственной задачи является транспонированной матрицей системы коэффициентов исходной задачи. Решение двойственной задачи может быть получено из исходной задачи и наоборот.
Несимметричные и симметричные двойственные задачи.
Пара двойственных задач называется несимметричной (I), если система ограничений исходной задачи задается в виде равенств, а двойственной задачи – в виде неравенств, причем во второй условие не отрицательности не налагается. Пара двойственных задач ЛП называется симметричной (II), если ограничения в обеих задачах записывается в виде неравенств, и накладывается условие не отрицательности.
Симметричную пару двойственных задач ЛП всегда можно свести к несимметричной паре путем введения дополнительных не отрицательных переменных. Теорема двойственности. Если одна из задач двойственной пары имеет оптимальный план, то и другая также имеет оптимальное решение, причем Lmax =Fmin(Lmin=Fmax). Если множество допустимых решений одной из задач не ограничено, то другая задач не ограничено, то другая задач не имеет решения.
Таблица 1.3.
Виды математических моделей двойственных задач.
| Тип | Исходная задача | Двойсвенная задача |
| I. | L(X)=CX-min AX=b X 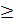 0 0 | F(Y)=BY-max ATY 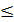 C C |
| II. | L(X)=CX-max AX=B X 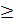 0 0 | F(Y)=BY-min ATY 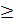 C C |
| I. | L(X)=CX-min AX 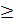 B X B X 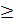 0 0 | F(Y)=BY-max ATY 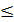 C Y C Y 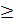 0 0 |
| II. | L(X)=CX-max AX=B X 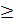 0 0 | F(Y)=BY-min ATY 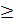 C Y C Y 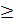 0 0 |
Правила построения пар двойственных задач.
– Число переменных двойственной задачи равно числу ограничений исходной задачи и наоборот.
– Свободные члены исходной задачи становятся коэффициентами линейной формы двойственной задачи и наоборот.
– Неравенства в системах ограничений прямой и двойственный задачах имеют противоположный друг друга смысл.
– Матрица коэффициентов двойственной задачи получается путем транспонирования матрицы коэффициентов исходной задачи.
– Если исходная задача решается на min, то двойственная – на max (и наоборот).
– На каждую переменную двойственной задачи налагается условие не отрицательности, если соответствующее ограничение исходной задачи является неравенством.
Идея двойственного симплекс- метода.
Двойственным симплекс – методом можно решать задачи ЛП, системы ограничений которых при положительном базисе пространства решений содержит свободные члены любого знака. Двойственных симплекс-метод позволяет уменьшить количество преобразований в системе ограничений, а следовательно и размеры расчетной симплекс-таблицы.
План Х, среди базисных компонент которого есть отрицательные, называется условно-оптимальным или псевдопланом, если условие оптимальности выполняется по индексной строке.
Решение задач линейного программирования двойственным симплекс-методом.
Двойственный симплекс-метод основан на теории двойственности задач ЛП и решает задачи, система ограничений которых при положительном базисе содержит свободные члены любых знаков. Этот метод позволяет уменьшить количество преобразований системы ограничений, а также размеры симплексной таблицы.
Рассмотрим следующую задачу ЛП: найти экстремум линейной формы
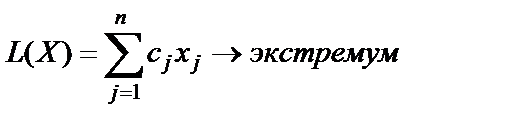 | (1.29) |
при следующих ограничениях:
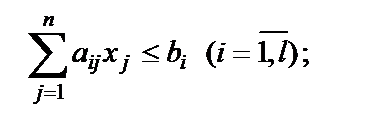 | (1.30) |
 | (1.31) |
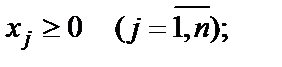 | (1.32) |
План X(x1,x2,…,xn), среди базисных компонент которого есть отрицательные, называется условно-оптимальным или псевдопланом, если по индексной строке выполнено условие оптимальности.
Если все компоненты базисного плана неотрицательны (при выполнении условия оптимальности по индексной строке), то полученный план является оптимальным.
Алгоритм двойственного симплекс-метода.
1. Систему ограничений (1.31) умножением на (-1) приводим к виду “£”:
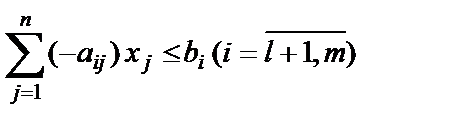 | (1.33) |
2. Строим первоначальный опорный план задачи (1.29-1.32). Для этого от системы неравенств переходим к системе уравнений, вводя дополнительные переменные, которые будут являться базисными. Заполняем первую симплекс-таблицу и анализируем коэффициенты индексной строки: а) если все коэффициенты индексной строки неотрицательны при решении задачи на максимум, или не положительны при решении задачи на минимум, то переходим к следующему шагу; б) если условие а) не выполнено, то симплекс- методом обеспечиваем выполнение этого условия. При этом элементы столбца q заполняются по правилу: неположительные элементы столбца свободных членов делятся на отрицательные коэффициенты ключевого столбца, а неотрицательные – на положительные.
3. Просматриваем элементы столбца свободных членов:
а) если все коэффициенты неотрицательны, то план оптимальный и задача решена;
б) если среди коэффициентов имеется хотя бы один отрицательный, то получен псевдоплан.
4. Из отрицательных коэффициентов столбца свободных членов берем наибольший по абсолютной величине. Этот элемент определяет ключевую строку, которая показывает, какая переменная должна выйти из базиса.
5. Коэффициенты индексной строки делим только на отрицательные элементы ключевой строки и заполняем строку q. Если задача ЛП на максимум, то элементы строки q берутся с обратным знаком.
6. Среди всех значений строки q выбираем наименьшее, которое определяет ключевой столбец. Ключевой столбец показывает, какая из переменных должна войти в базис. На пересечении ключевой строки и столбца находим генеральный элемент.
7. Выполняем обычную симплекс-процедуру по переходу к следующей таблице и возвращаемся к шагу 3.
Решение контрольного примера.
Найти 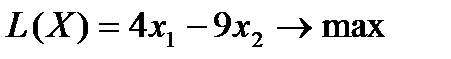 при следующих ограничениях:
при следующих ограничениях:
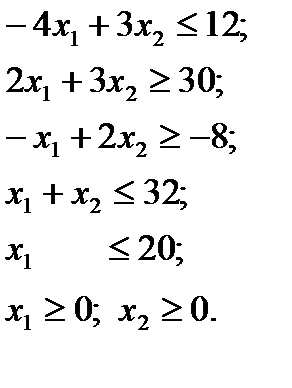
Систему ограничений приводим у виду " 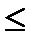 ":
":
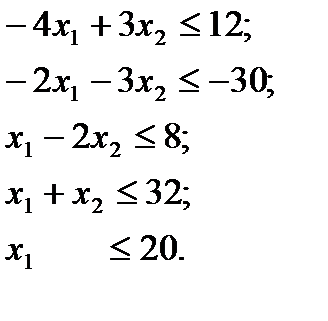
От системы неравенств переходим к системе уравнений:
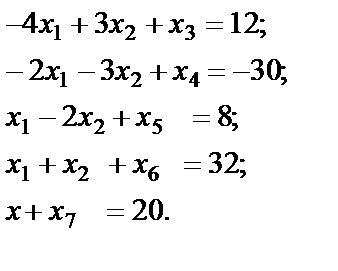
Заполняем первую симплекс-таблицу (таблица 1.4.) и анализируем индексную строку.
Так как в индексной строке в столбце X1, имеется отрицательный коэффициент (-4), то условие а) не выполняется и столбец Х1 выбираем за ключевой. Заполняем столбец q:
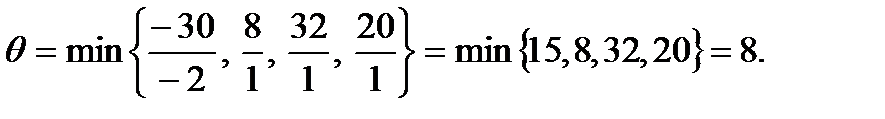
Строка Х5 – ключевая. Генеральный элемент равен 1. По обычной симплекс-процедуре переходим к таблице 2.
1. Во второй симплекс-таблице (таблица 1.4) в индексной строке все коэффициенты неотрицательны, т.е. условие а) выполнено, но среди свободных членов есть отрицательный (-14), т.е. получили псевдоплан.
2. Строку Х4 выбираем за ключевую.
3. Заполняем строку q.
4. В данном случае имеем единственное отношение, равное 1/7. Столбец, содержащий Х2, принимаем за ключевой. На пересечении находим генеральный элемент (-7).
5. По обычному правилу переходим к заполнению следующей таблицы и к шагу 3. В третьей симплекс-таблице (таблица 1.4) все коэффициенты столбца свободных членов неотрицательны, следовательно, задача решена и получен оптимальный план Х(12,2,5,4,0,0,18,8), Lmax=30.
Таблица 1.4.
| № таб-лицы | Базис. Пере-мен. | Сво-бод. члены | X1 | X1 | X1 | X1 | X1 | X1 | X1 | å | q |
| X3 | -4 | - | |||||||||
| X4 | -30 | -2 | -3 | -34 | |||||||
| X5 | -2 | ||||||||||
| X6 | |||||||||||
| X7 | |||||||||||
| L(X) | -4 | Max | |||||||||
| X3 | -5 | - | |||||||||
| X4 | -14 | -7 | -18 | - | |||||||
| X1 | -2 | - | |||||||||
| X6 | -1 | - | |||||||||
| X7 | -1 | - | |||||||||
| L(X) | - | ||||||||||
| q | Max | 1/7 | - | - | - | - | - | - | Max | ||
| X3 | -5/7 | 18/7 | 396/7 | - | |||||||
| X2 | -1/7 | -2/7 | 18/7 | - | |||||||
| X1 | -2/7 | 3/7 | 92/7 | - | |||||||
| X6 | 3/7 | -1/7 | 135/7 | - | |||||||
| X7 | 2/7 | -3/7 | 62/7 | - | |||||||
| L(X) | 1/7 | 30/7 | 241/7 | Max |
