Решение задач линейного программирования симплекс-методом.
Рассмотрим задачу ЛП, в которой система ограничений задана в виде неравенств смысла "≤".
Требуется найти экстремум функции
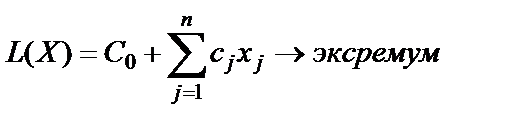 | (1.23) |
при следующих ограничениях:
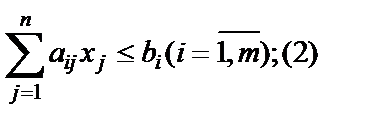 | (1.24) |
 |
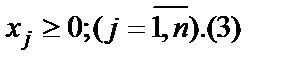При использовании симплекс-метода процесс решения проще выполняется в симплексных таблицах.
Алгоритм симплекс-метода.
Построим первоначальный опорный (или базисный) план. От системы неравенств переходим к системе уравнений, вводя дополнительные неотрицательные переменные:
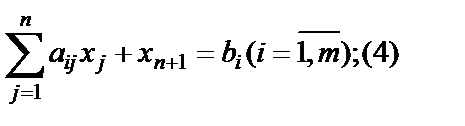 | (1.25) |
Дополнительные неотрицательные переменные
 |
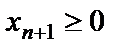будут являться базисными, т.к. последние m столбцов матрицы коэффициентов системы уравнений (1.25) представляют столбцы единичной матрицы, которые являются линейно-независимыми. Следовательно, неотрицательные переменные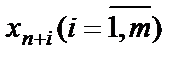 
соответствующие этим столбцам, по определению будут базисными переменными.
Составляем симплексную таблицу, которая состоит из столбцов базисных переменных, свободных членов, контрольных сумм и θ. Последняя строка симплекс-таблицы, называемая индексной, заполняется коэффициентами линейной формы (1.23), взятыми с противоположными знаками (кроме С0).
Проверяем выполнение признака оптимальности для построенного плана. Для того, чтобы план X=(x1, x2, …, xn) был оптимальным, достаточно, чтобы все коэффициенты индексной строки (кроме C0) были неотрицательны при решении задачи ЛП на максимум и не положительны на минимум.
Если признак оптимальности выполняется, то выписываем решение. В столбцах базисных переменных и свободных членов расположены соответственно компоненты и значения построенного оптимального плана, на пересечении индексной строки и столбца свободных членов – экстремальное значение линейной формы L(X).
Если признак оптимальности не выполняется, то при решении задачи на максимум из отрицательных коэффициентов индексной строки выбираем наибольший по абсолютной величине, а при задаче на минимум из положительных коэффициентов индексной строки выбираем наибольший. Столбец, соответствующий выбранному наибольшему коэффициенту, называется ключевым. Ключевой столбец показывает, какая переменная войдет в базис.
Вычисляем отношения столбца свободных членов только к положительным элементам ключевого столбца (если таковых не имеется, то задача ЛП решения не имеет) и записываем их в столбец θ. Из всех элементов столбца θ выбираем наименьший. Строку симплексной таблицы, содержащую наименьшее значение θ, назовем ключевой. Ключевая строка показывает, какая переменная выйдет из базиса.
На пересечении ключевого столбца и ключевой строки находится генеральный элемент.
Переходим к составлению следующей симплекс-таблицы. Для этого выполняем следующие действия:
a) свободную переменную, соответствующую ключевому столбцу, вводим в базисные переменные, а базисную переменную, соответствующую ключевой строке, переводим в свободные;
b) заполняем направляющую строку новой таблицы, которая составляется из элементов ключевой строки предыдущей таблицы путем деления на генеральный элемент;
c) для перевода переменной, соответствующей ключевому столбцу, из свободной в базисные нужно исключить ее из всех строк, кроме направляющей. Для этого методом Жордана – Гаусса накапливаем нули во всех остальных клетках столбца, соответствующего ключевому столбцу предыдущей таблицы.
Процесс вычислений продолжаем в симплексных таблицах до выполнения признака оптимальности.
Замечание.
Если при оптимальном плане в индексной строке имеется нуль, а столбец, соответствующий ему, содержит не менее двух ненулевых элементов, из которых хотя бы один положительный, то задача ЛП имеет множество оптимальных планов. Действительно, столбец, соответствующий нулю в индексной строке, выбирается за ключевой и строится новый оптимальный план с другим набором базисных переменных, но с тем же самым значением L(X). Тогда по основной теореме ЛП любая выпуклая комбинация этих планов будет тоже оптимальной, следовательно, задача ЛП имеет множество оптимальных планов.
Решение контрольного примера.
Найти максимум функции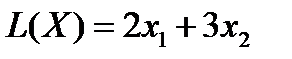 
при следующих ограничениях:
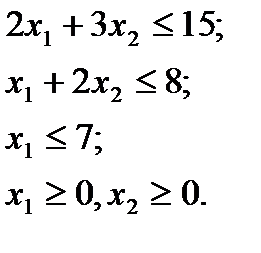
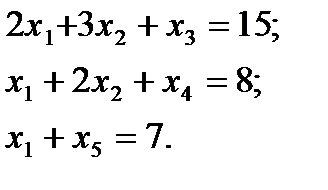
1. Вводя дополнительные неотрицательные переменные x3, x4, x5, переходим к системе уравнений
Составим первую симплекс-таблицу с базисными переменными x3, x4, x5. Получаем первоначальный опорный план
X1(0, 0, 15, 8, 7) и L(X1)=0.
2. Проверим полученный план на оптимальность. Так как задача на максимум, то при оптимальном плане в индексной строке не должно быть отрицательных чисел. В индексной строке первой симплекс-таблицы (таблицы 1.1.) имеются два отрицательных коэффициентов.
3. Выбираем среди отрицательных коэффициентов индексной строки наибольший по абсолютной величине: max{/-2/, /-3/}=/-3/. Следовательно, столбец, содержащий переменную x2, будет являться ключевым. Отметим его стрелкой, которая указывает, что переменная x2 из свободных должна перейти в базисные.
4. Для нахождения ключевой строки вычисляем значения θ: элементы столбца свободных членов делим только на положительные элементы ключевого столбца x2. Получаем столбец θ(5,4,-). Находим min{5,4}=4. Следовательно, ключевой строкой будет строка, соответствующая базисной переменной x4. Обозначим эту строку стрелкой, показывающей, что x4 должна из базисных переменных перейти в свободную.
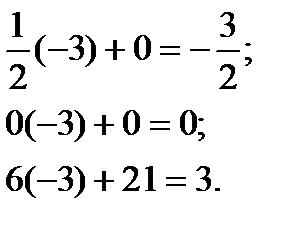
На пересечении ключевой строки и столбца стоит генеральный элемент 2. Выделяем его кружком.
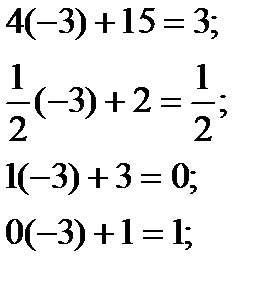
5. После этого переходим к составлению следующей симплекс-таблицы. Заполняем направляющую строку x2, которая получается из ключевой строки x4 предыдущей таблицы путем деления на генеральный элемент 2. В остальных клетках столбца второй симплекс-таблицы (таблица 1.1.) должны накопиться нули, оперируя с элементами направляющей строки.
Так, например, для получения нуля в этом столбце в строке x3, умножим все элементы направляющей строки второй симплекс-таблицы (таблица 1.1.) на соответствующий элемент ключевого столбца первой симплекс-таблицы (таблица 1.1.), взятый с противоположным знаком, т.е. на (-3), и сложим с соответствующими элементами строки x3 первой симплекс-таблицы (таблица 1.1.):
Сумма всех элементов этой строки равна 3, следовательно, все элементы строки x3 вычислены правильно.
Строку x5 переписываем во вторую симплекс-таблицу (таблица 1.1.) без изменения, т.к. в ключевом столбце она имеет нуль. Для получения нуля в оставшейся клетке столбца x2 умножим направляющую строку на 3 и сложим с соответствующими элементами строки L(X) первой симплекс-таблицы (таблица 1.1.). В результате заполнения второй симплекс-таблицы (таблица 1.1.) получим второе базисное решение, которое имеет улучшенное значение линейной формы, но не является оптимальным, так как в индексной строке второй симплекс-таблицы (таблица 1.1.) имеется отрицательное число. Решение необходимо продолжить, возвращаясь к шагу 2.
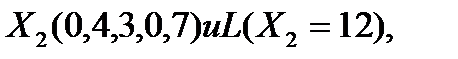
В третьей симплекс-таблице (таблица 1.1.) в индексной строке все коэффициенты неотрицательны, следовательно, X3(6, 1, 0, 0, 1) являются оптимальным решением и L(X3)-Lmax=15.
Но анализ индексной строки показывает, что полученный оптимальный план не является единственным.
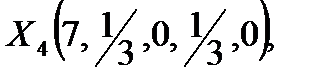
Если за ключевой столбец третьей симплекс-таблицы (таблица 1.1.) принять столбец x4 и проделать всю необходимую симплекс-процедуру, то получим другой оптимальный план, но с тем же самым значением Lmax=14 (таблица 1.1.).
Зная два оптимальных решения, можно построить их множество:
где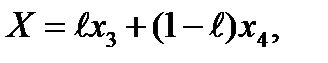 
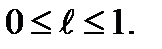
Полное решение этого примера приводится в симплексной таблице 1.1.
Таблица 1.1.
| № | Базисные переменные | Свободные члены | X1 | X2 | X3 | X4 | X5 | Σ | θ |
| 1. | X3 | ||||||||
| ← X4 | |||||||||
| X5 | - | ||||||||
| L(X) | -2 | -3↑ | -5 | max | |||||
| 2. | ← X3 | 1/2 | 3/2 | ||||||
| X2 | 1/2 | ||||||||
| X5 | |||||||||
| L(X) | -1/2 ↑ | 3/2 | max | ||||||
| 3. | X1 | -3 | - | ||||||
| X2 | -1 | ½ | |||||||
| X5 | -2 | 1/3 | |||||||
| L(X) | 0↑ | max | |||||||
| 4. | X1 | ||||||||
| X2 | 1/3 | 1/3 | -2/3 | ||||||
| X4 | 1/3 | -2/3 | 1/3 | ||||||
| L(X) | max |