Графический метод решения задач линейного программирования.

Графический метод используется для решения задач ЛП, когда n=2 или n=3, и также для задач, система ограничений которых содержит n неизвестных и m линейно-независимых уравнений, если n и m связаны соотношением n-m=2. Наиболее наглядным является решение задач ЛП в двумерном пространстве. Сформулируем задачу для этого случая:

Найти экстремум функции цели:

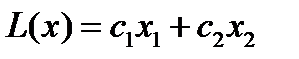(1.8)

при следующих ограничениях:

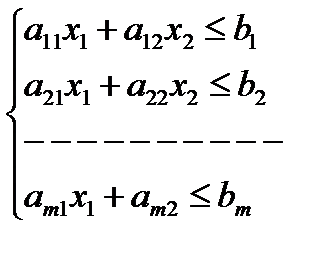	(1.9)
xj 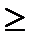0,j=1,2	(1.10)

Алгоритм графического метода.

Строим многоугольник допустимых решений (быть может и неограниченную область), все точки которого удовлетворяют исходной системе ограничений (1.9) - (1.10). Для этого для систем неравенств (1.9) и (1.10) записываем соответствующие граничные прямые и проводим их на плоскости.

Каждая из граничных прямых делит плоскость на две полуплоскости. Для определения полуплоскости решения необходимо координаты любой точки плоскости подставить в соответствующее неравенство. Если эта точка удовлетворяет неравенству, то необходимо за полуплоскость решения взять ту часть плоскости, где лежит эта точка. Полуплоскость решения обозначаем стрелками. Аналогично строится область решений всех неравенств и определяется их общая часть.

Проводим начальную прямую L₀ из семейства параллельных прямых (1.8) и градиент Ñ(c₁, c₂), указывающий направление возрастания линейной формы (1.8).

Перемещаем начальную прямую L₀ параллельно самой себе до тех пор, пока она не займет опорного положения, т.е. положения, когда многоугольник решений будет лежать по одну сторону от нее и будет иметь с этой прямой хотя бы одну общую точку.

Тогда первое опорное положение, которое принимает начальная прямая L₀ по направлению Ñ(c₁, c₂), является L_min, а второе L_max.

Определяем координаты точек экстремума, для чего решаем совместно уравнения тех граничных прямых, при пересечении которых образовались эти точки, и вычисляем значения функции цели (1.8) в этих точках.

Замечание: В тех случаях, когда опорная прямая совпадает с одной из сторон многоугольника решений, функция цели (1.8) принимает экстремальное значение одновременно в двух угловых точках X₁⁰ и X₂⁰.

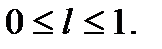
Тогда на основании теоремы о множестве оптимальных планов линейная форма (1.8) принимает одинаковые экстремальные значения во всех точках, являющихся выпуклой линейной комбинацией точек X₁⁰ и X₂⁰, т.е. во всех точках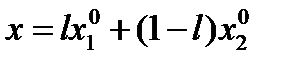

Решение контрольного примера.

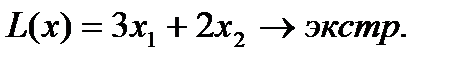
Найти максимум и минимум функции цели

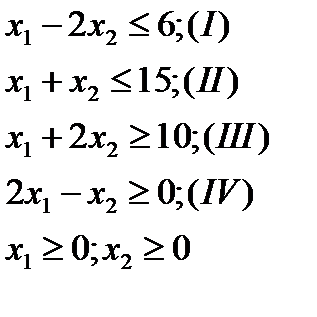
при следующих ограничениях:

1. Построим многоугольник решений. Запишем уравнения граничных прямых (для удобства построения уравнения этих прямых, где это возможно, представим в виде уравнений в отрезках, т.е. x₁/a +x₂/b=1):

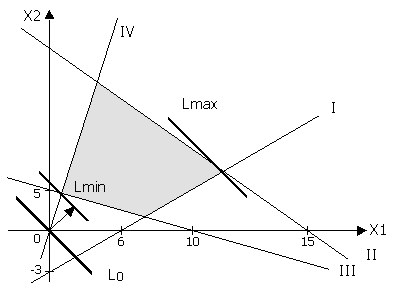
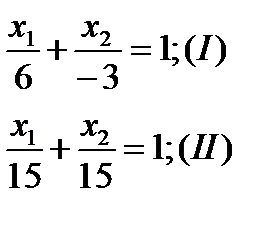
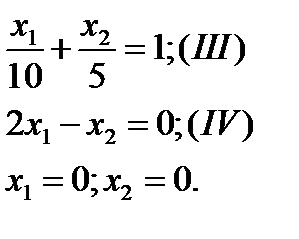
Проведем 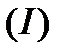граничную прямую, которая на оси Ox₁, отсекает отрезок, равный 6, а на оси Ox₂ – (-3). Определим полуплоскость решений. Для этого возьмем т.О(0,0) и подставим ее координаты в соответствующее неравенство

1. Это неравенство справедливо, поэтому берем ту плоскость, где лежит т.о (0,0), отмечаем ее стрелками. Аналогично определяем полуплоскости решений для остальных неравенств. В результате многоугольник решений получим в виде четырехугольника АВСД.

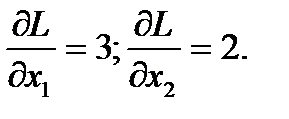
Проводим начальную прямую L₀, т.е. 3x₁+2x₂=0. Это уравнение прямой, проходящей через начало координат. Для построения градиента функции цели вычисляем ее частные производные.

Откуда направление наискорейшего возрастания функции цели определяется вектором Ñ(3,2).

2. Перемещаем начальную прямую параллельно самой себе в направлении градиента Ñ(3,2). Опорные прямые из семейства L(X) проходят через вершины А и С: в точке С функция цели достигает максимума, а точка А функция цели достигает минимума.

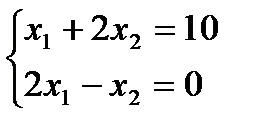
3. Определяем координаты экстремальных точек. Для определения координат вершины А необходимо решить систему двух уравнений граничных прямых (III) и (IV):

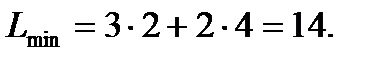
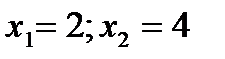
Следовательно, точка А имеет координаты (2,4), а значение 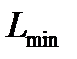=14. Аналогично определяем координаты точки С (12,3) и значение целевой функции .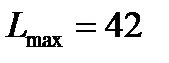