А.У. Калижанова, Н.И. Аманжолова, А.И. Ерзин, Ю.А. Кочетов

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РЕСПУБЛИКИ КАЗАХСТАН

Казахский национальный исследовательский технический университет

имени К.И. Сатпаева

А.У. Калижанова, Н.И. Аманжолова, А.И. Ерзин, Ю.А. Кочетов

МЕТОДЫ ОПТИМИЗАЦИИ И ИССЛЕДОВАНИЕ ОПЕРАЦИЙ

Учебное пособие

Алматы 2016

УДК 519.85(075)

ББК В173

К 519

K 519

А.У. Калижанова, Н.И. Аманжолова, А. И. Ерзин, Ю. А. Кочетов,

Методы оптимизации и исследование операций: учеб. пособие / КазНИТУ. – Алматы: КазНИТУ, 2016. – 103 с.

ISBN

Учебное пособие состоит из основного курса «Методы оптимизации и исследование операций». Пособие содержит необходимые определения, утверждения, алгоритмы, примеры и упражнения, посвящено методам поддержки принятия оптимальных решений. Пособие включает в себя разделы по синтезу остовных деревьев и деревьев Штейнера, а также по построению оптимальных путей и контуров.

Предназначено для студентов и магистрантов, обучающихся по специальности 5B060200 – Информатика, 6М060200 – Информатика КазНИТУ имени К.И. Сатпаева, студентов механико-математического факультета НГУ, а также для всех, кто желает освоить курс самостоятельно.

УДК

ББК

Рецензенты:

Амиргалиев Е.Н., доктор техн. наук, профессор, зав.кафедрой «Компьютерная инженерия» Университета имени С. Демиреля.

Имангалиев Ш.Н., канд. техн. наук., доцент, зав.кафедрой «Информационные системы» Алматинский университет энергетики и связи.

Балгабаева Л.Ш., канд. техн. наук., доцент, зав.кафедрой «Информационные технологии» КазНИТУ им. К.И.Сатпаева.

ISBN	© А. У. Калижанова, Н.И.Аманжолова, А. И. Ерзин, Ю. А. Кочетов, 2016
	© КазНИТУ, 2016

ОГЛАВЛЕНИЕ

Введение
1. МЕТОДЫ ОПТИМИЗАЦИИ
1.1.	Общая задача линейного программирования
1.2.	Графический метод решения задач линейного программирования
1.3.	Симплексный метод решения задачи линейного программирования
1.4.	Отыскание оптимального плана
1.5.	Решение задач линейного программирования симплекс-методом
1.6.	Решение задач линейного программирования методом искусственного базиса
1.7.	Двойственность в ЛП
1.8.	Транспортная задача линейного программирования
2. ПОСТРОЕНИЕ ОСТОВНЫХ ДЕРЕВЬЕВ
2.1.	Минимальное остовное дерево. Алгоритмы Прима, Краскала, Борувки
2.2.	Остовные деревья и их приложения
2.3.	Примеры и упражнения
3. ЗАДАЧИ ПОСТРОЕНИЯ КРАТЧАЙШИХ ПУТЕЙ
3.1.	Алгоритм Дейкстры
3.2.	Алгоритм Беллмана–Форда
3.3.	Алгоритм Флойда–Уоршелла
3.4.	Примеры и упражнения
4. ЗАДАЧА ШТЕЙНЕРА
4.1.	Постановки задачи Штейнера и ее сложность
4.2.	Приближенные алгоритмы
4.3.	Некоторые задачи синтеза сетей, использующие деревья Штейнера
4.4.	Примеры и упражнения
5. ЗАДАЧА КОММИВОЯЖЕРА
5.1.	Вычислительная сложность
5.2.	Конструктивные алгоритмы
5.3.	Нижние оценки
5.4.	Локальный поиск
5.5.	Метаэвристики
5.6.	Упражнения
Библиографический список

ВВЕДЕНИЕ

Данное пособие посвящено изучению курса «Методы оптимизации и исследование операций». Рассматриваются алгоритмы, которые позволяют эффективно строить оптимальные маршруты – подграфы заданных графов, обладающие заданными экстремальными свойствами. Остовные деревья, кратчайшие пути в графах, коммуникационные сети и гамильтоновы циклы будут в этом пособии в центре внимания. Наряду с классическими алгоритмами дискретной оптимизации, мы познакомимся и с новыми подходами к построению алгоритмов, заимствованными у природы: генетические алгоритмы, имитация отжига и др.

Если не оговорено дополнительно, то далее будут использоваться следующие обозначения:

– множество целых неотрицательных чисел;

– множество n-мерных неотрицательных целочисленных векторов;

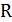– множество вещественных чисел;

– множество n-мерных вещественных векторов

– множество n-мерных булевых векторов

– мощность множества ;

– целая часть числа ;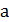

– минимальное целое число, которое не меньше ;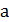

– оптимальное решение;

∎ – конец доказательства.

Для удобства читателя напомним определения некоторых базовых понятий, которые понадобятся в дальнейшем.

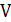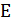Определение 1. Графом называется пара множеств и , где – множество вершин, а – множество ребер графа. Для изображения вершины, как правило, используется точка, а для изображения ребра – отрезок линии между двумя точками. Упорядоченная пара вершин определяет дугу и изображается стрелкой, которая заканчивается в конечной вершине дуги.

Определение 2. Две вершины, связанные ребром, являются смежными. Если вершина является одним из концов ребра, то эти вершина и ребро инцидентны друг другу. Степень вершины равна числу инцидентных ей ребер. Степень графа совпадает с максимальной степенью вершин.

Определение 3. Простой цепью называется ациклический связный подграф степени 2. Ориентированная цепь, в которой все дуги ориентированы от начала к концу пути, называется путем.

Определение 4. Связный подграф, все вершины которого имеют степень 2, называется циклом. Цикл, включающий все вершины графа, называется гамильтоновым.

Определение 5. Граф, каждому ребру которого приписано число – «вес», называется взвешенным. Сумма весов ребер, входящих в подграф, называется весом подграфа.

Определение 6. Количество символов в стандартном (двоичном) представлении данных индивидуальной задачи назовем длиной входа и обозначим

Определение 7. Пусть алгоритм 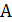решает проблему и –количество элементарных операций (арифметические операции и операции сравнения), выполняемых алгоритмом 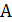при решении индивидуальной задачи . Тогда функция называется трудоемкостью алгоритма .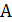

Алгоритм 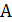называется полиномиальным, если его трудоемкость где 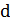– целое положительное число.

Алгоритмы, трудоемкость которых не ограничена полиномом от длины входа, называются экспоненциальными.

В теории вычислительной сложности принято рассматривать задачи распознавания (свойств), то есть задачи, в которых возможным ответом является«Да» или «Нет». Например, правда ли, что заданный граф является деревом? Среди задач распознавания принято выделять классы P и NP. Напомним, что класс P состоит из задач распознавания, разрешимых за полиномиальное время. Класс NP является более широким. Он включает в себя все задачи распознавания, в которых ответ «Да» может быть проверен за полиномиальное время. Задача принадлежит этому классу, если, даже не умея ее решать, можно «легко» проверить ответ, подглядев его или найдя в Интернете. При этом достаточно уметь проверять только ответ «Да». Иногда проверка ответа «Да» может быть легче или сложнее проверки ответа «Нет». Рассмотрим задачу о гамильтоновости графа: задан простой неориентированный граф, требуется узнать, содержит ли он гамильтонов цикл? Покажем, что эта задача принадлежит классу NP. Предположим, что граф действительно гамильтонов, и кто-то подсказал нам ответ, указав один из таких циклов. Можно ли проверить эту подсказку за полиномиальное время? Для этого нужно проверить, что указанный набор ребер образует простой цикл, и он покрывает все вершины. Очевидно, что это «легко» сделать и, следовательно, задача принадлежит классу NP. Заметим, что ответ «Нет» проверить здесь куда труднее. Говорят, что задача распознавания принадлежит классу co-NP, если ответ «Нет» можно проверить за полиномиальное время. Легко показать, что следующая задача принадлежит классу co-NP. Задан простой неориентированный граф, правда ли, что он не является гамильтоновым? Ответ «Нет» означает гамильтоновость графа, а это можно легко проверить.

В классе P можно проверить с полиномиальной трудоемкостью любой ответ, и, значит, P Í NP. Доказать или опровергнуть обратное включение пока никому не удается. На сегодняшний день это одна из центральных проблем математики – «задача тысячелетия» (http://www.claymath.org/millennium/). За ее решение Американское математическое общество обещает приз – миллион долларов.

Многолетние интенсивные исследования подсказывают, что P ≠ NP. Косвенным доказательством этой гипотезы служит тот факт, что в классе NP обнаружены так называемые NP-полные задачи.

Определение 8. Задачу из класса NP называют NP-полной, если существование полиномиального алгоритма для ее решения влечет существование полиномиальных алгоритмов для всех задач из класса NP.

К настоящему времени известно огромное количество NP-полных задач [7, 17]. Однако ни для одной из них не удалось разработать точный полиномиальный алгоритм.

Определение 9. Приближенным алгоритмом решения задачи является алгоритм, строящий допустимое решение. Оценкой точности приближенного алгоритма 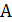назовем такое число , что отношение не превосходит для любой индивидуальной задачи на минимум и не менее для любой индивидуальной задачи на максимум. Здесь – значение целевой функции на оптимальном решении задачи , а – значение функционала на решении, построенном алгоритмом 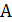. При этом алгоритм 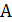называется – приближенным.

Задача из класса NP может быть решена экспоненциальным алгоритмом, который просто перебирает всех потенциальных кандидатов. Мы предполагаем, что их размер ограничен полиномом от размера входа. Оказывается, что бывают задачи, которые не решаются вообще никаким алгоритмом (ни полиномиальным, ни экспоненциальным, ни ещё более долго работающим); их называют неразрешимыми (unsolvable) [38].

МЕТОДЫ ОПТИМИЗАЦИИ

Выпуклые множества

Пусть на плоскости х₁Ох₂ заданы две точки: А₁ (х₁⁽¹⁾; х₂⁽¹⁾) и А₂ (х₁⁽²⁾; х₂⁽²⁾), определяющие прямолинейный направленный отрезок _. Найдем координаты произвольной внутренней точки А (х₁; х₂) данного отрезка через координаты его концов.

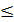Векторы = (х₁- х₁⁽¹⁾; х₂- х₂⁽¹⁾) и = (х₁⁽²⁾- х₁⁽¹⁾; х₂⁽²⁾- х₂⁽¹⁾) параллельны и одинаково направлены, поэтому = t ( ), где 0 t 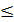1, или х₁- х₁⁽¹⁾=t(х₁⁽²⁾- х₁⁽¹⁾), х₂- х₂⁽¹⁾= t(х₂⁽²⁾- х₂⁽¹⁾). Отсюда х₁=(1-t) х₁⁽¹⁾+ tх₁⁽²⁾, х₂ =(1-t) х₂⁽¹⁾ + t х₂⁽²⁾. Полагая 1- t₁= , t= получим

(1.5)

Учитывая, что в (1,5) координаты точки А являются суммами одноименных координат точек А₁ и А₂, умноженными соответственно на числа , окончательно получаем:

	(1.6)
	(1.7)

Точка А, для которой выполняются условия (1.6) и (1.7), называется выпуклой линейной комбинацией точек А₁ и А₂. При и точка А совпадает с концом отрезка А₁, при и с концом отрезка А₂. Таким образом, если t пробегает все значения от 0 до 1, то точка А описывает отрезок _. Точки А₁ и А₂ называются угловыми и крайними точками отрезка _.

Из определения линейной выпуклой комбинации точек очевидно, что угловая точка не может быть представлена как выпуклая линейная комбинация двух других точек отрезка. Соотношения (1.6) и (1.7) верны независимо от размерности пространства.

Пусть имеется n точек А₁, А₂,…,А_n. Точка А является их выпуклой линейной комбинацией, если выполняются условия

Множество точек называется выпуклым, если оно вместе с любыми двумя точками содержит и их произвольную выпуклую линейную комбинацию.

Геометрическая интерпретация задач ЛП.

Рассмотрим задачу ЛП, система ограничений которой задана в виде неравенств.

Такой подход удобен, когда число неизвестных равно 2.

Пример: экстремум (1.5)

(1.6)

xj 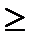0,j=1,2

(1.7)

Если система (1.6) совместна, то она должна иметь хотя бы один план. При этом каждое соотношение из (1.6) геометрически представляет собой полуплоскость. Общая часть всех полуплоскостей решений задачи (1.6)-(1.7), может оказаться точкой, отрезком, многоугольником ограниченным или неограниченной многоугольной плоскостью.

Геометрически задача ЛП представляет собой отыскание такой точки многогранника решений, координаты которой доставляют экстремум целевой функций, причем все точки многоугольника решений являются допустимыми решениями.

Свойства решений задач ЛП.

Теорема 1. Множество всех планов задачи ЛП выпукло.

Теорема 2.Линейная функция задачи ЛП достигает своего экстремального значения в угловой точке многогранника решений. Если целевая функция достигает экстремального значения более чем в 1 угловой точке, то она достигает того же значения в любой точке, являющейся выпуклой линейной комбинацией этих точек.

Теорема 3.Пусть имеем задачу (1.1)-(1.3). Если система векторов линейно независима и удовлетворяет соотношению (1.2) при выполнении (1.3), то вектор Х является угловой точкой многогранника решений.

Теорема 4.Если угловая точка многогранника решений, то векторы в разложении (1.4) являются линейно независимыми при x 0 с положительными компонентами [1].

Примеры и упражнения

Пример 2.1. Построить МОД в графе, изображенном на рис. 2.1a (рядом с ребрами указаны их веса), с помощью алгоритма Прима.

Решение. Положим 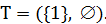Тогда метки вершин 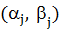, , 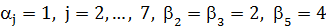остальные 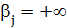. Вершины 2 и 3, ближайшие к T, добавим, например, вершину 2, получив 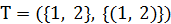, и пересчитаем метки для вершин 3, …, 7. Получим 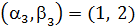, , 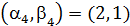, 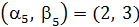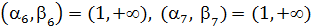Теперь ближайшая к T вершина 4, добавим ее: 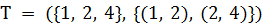. Продолжая процесс, добавим последовательно вершины 5, 3, 7 и 6 вместе с ребрами (4 ,5), (1, 3), (5, 7) и (3, 6). МОД изображено на рис. 1.1b, и его вес равен 14.

Рисунок-2.1.a) граф; b) МОД

Пример 2.2. Найти количество остовных деревьев графа, изображенного на рис. 2.1a, степени которых не превосходят 2.

Решение. Перенумеруем ребра. Очевидно, ребро 1 = (5, 7) войдет во все остовные деревья. Можно построить двоичное дерево решений, начиная с ребра 1, включая (если это не приводит к циклу или превышению допустимой степени вершин) или не включая очередное ребро. В результате получим три гамильтоновых пути. Один из них изображен на рис. 2.1b, два других – на рис. 2.2.

Рисунок-2.2. Два остовных дерева степени 2

Упражнение 2.1. Доказать, что алгоритмы Прима, Краскала и Борувки строят МОД.

Упражнение 2.2. Показать, что в дереве, имеющем две и более вершины, существует как минимум две вершины степени 1.

Упражнение 2.3. Найти такое остовное дерево графа, показанного на рис. 2.1a, в котором максимальный вес ребра минимален.

Упражнение 2.4. Найти МОД графа, показанного на рис. 2.1a, используя алгоритмы Краскала и Борувки.

Упражнение 2.5. Найти все МОД графа, показанного на рис. 2.3.

Рисунок-2.3. Взвешенный граф
(рядом с каждым ребром указан его вес)

ЗАДАЧА ШТЕЙНЕРА

Пусть на плоскости расположены три точки, расстояния между которыми определяются евклидовой метрикой, и требуется связать эти точки с помощью МОД. Построенное дерево показано на рис. 4.1a, и его длина (сумма длин ребер) равна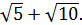

b)

a)

Рисунок-4.1.Минимальное остовное дерево(a)и дерево Штейнера(b)

Введем дополнительную (промежуточную) точку и соединим исходные точки с промежуточной точкой. В результате получим связывающее дерево меньшей длины 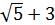(по сравнению с МОД) (рис. 4.1b). Это дерево является геометрическим (или метрическим) деревом Штейнера, и в него вошла одна дополнительная точка (2, 2) – вершина Штейнера. При построении метрического дерева Штейнера для уменьшения длины дерева можно использовать любые дополнительные точки на плоскости.

Далее будем рассматривать задачу Штейнера на графах, формулировка которой приводится в следующем разделе. В последней задаче точки Штейнера выбираются из заданного множества вершин графа.

Приближенные алгоритмы

Очевидно, МОД является приближенным решением задачи Штейнера. При этом для метрического случая, когда точки (вершины) расположены на плоскости, отношение ,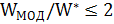
где 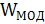– вес минимального остовного дерева, а 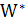– минимальная длина дерева Штейнера. Алгоритм Прима (Краскала) строит 2-приближенное решение задачи Штейнера с полиномиальной трудоемкостью.

Известен более сильный результат: 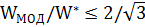, для метрической задачи с евклидовой метрикой. Предложено также несколько алгоритмов, которые строят 2-приближенное решение задачи Штейнера на произвольных графах. Например, достаточно найти кратчайшие пути между каждой парой вершин графа, перейти к вспомогательному графу без промежуточных вершин с длинами ребер, равными длинам кратчайших путей, и построить МОД. Это и будет 2-приближенное решение для исходной задачи Штейнера.

Опубликован ряд работ, в которых предложены алгоритмы с меньшей оценкой точности, например, алгоритм строящий 1.55-приближенное решение для точек, расположенных на плоскости, расстояния между которыми задаются прямоугольной (манхэттеновской) метрикой [9]. В этом случае дерево Штейнера состоит из множества вертикальных и горизонтальных отрезков, соединяющих терминалы и промежуточные точки. Однозначно определяется минимальный прямоугольник, в котором находятся все терминалы, и его стороны параллельны осям (прямоугольник ABCD на рис. 3.3). Очевидно, все ребра МДШ не выходят за пределы этого прямоугольника. В 1966 г. Ханан показал [10], что существует МДШ, в которое входят только узлы решетки, полученной от пересечения горизонтальных и вертикальных прямых, проходящих через терминалы, – решетка Ханана (рис. 3.3).

Рисунок-4.3. Минимальное дерево Штейнера (жирные линии) на решетке Ханана

В 1976 г. Хванг [11] показал, что МОД является 3/2-приближен-ным решением. В 1992 г. Зеликовский [12] разработал алгоритм построения прямоугольного дерева Штейнера с оценкой точности 11/8, первый эвристический алгоритм, который строит решение лучше МОД.

Примеры и упражнения

Пример 4.1.Пусть требуется связать МДШ четыре точки расположенные на плоскости попарно симметрично относительно горизонтальной прямой (рис. 4.6).

120°

120°

Рисунок-4.6. Вершины степени 3 – точки Штейнера

Решение. Из свойств геометрического МДШ следует, что число точек Штейнера не превосходит 2, и инцидентные им ребра образуют угол в 120°. Проведем горизонтальную прямую на одинаковом расстоянии между левыми и правыми точками. Из каждой точки проведем прямую, пересекающуюся с горизонтальной прямой под углом 120°. Точки пересечения – точки Штейнера. МДШ построено, в него вошли 2 точки Штейнера (см. рис. 4.6).

Пример 4.2. Пусть вершины графа расположены в узлах единичной решетки на рис. 4.7. Требуется связать терминалы
2-приближенным деревом Штейнера с использованием прямоугольной метрики L₁.

Решение. Построим сначала решетку Ханана, проведя горизонтальные и вертикальные линии, проходящие через терминалы (рис. 4.7a). Найдем длины кратчайших путей между каждой парой терминалов и построим МОД (рис. 3.7b). На решетке представление построенного дерева не однозначно, но любое представление будет 2-приближенным решением задачи Штейнера. На рис. 3.7a представлено дерево, которое является МДШ.

Рисунок-4.7.Решетка Ханана (a) и минимальное остовное дерево (b)

Пример 4.3. Для иллюстрации работы метода

решения ЗГТ приведем пример. Пусть имеется 11 сетей, 3 слоя и решетка 5´2. Все элементы СБИС расположены на первом (нижнем) слое, межслойные соединения имеют высокую пропускную способность, нулевую емкость и сопротивление 0.00937. Второй слой используется для осуществления «вертикальных» соединений (то есть параллельных оси 0y), линия связи (соответствующее ребро глобального графа) имеет пропускную способность 16, удельную емкость 0.470431, удельное сопротивление 0.016209. Межслойные соединения между слоями 2 и 3 имеют высокую пропускную способность, нулевую емкость и сопротивление 0.00781. Третий уровень используется для соединений, параллельных оси 0x, имеет пропускную способность – 12, удельную емкость 0.456122 и удельное сопротивление 0.010763.

На рис. 4.8 приведен результат работы метода, который построил трассировку с плотностью (максимальным количеством соединений на одном ребре графа) 5. Время прихода сигнала (AT) в основной выход 12 – это 34 ps (пикосекунды), и AT в основной выход 13 - 36 ps. На рис. 3.9 приведена проекция деревьев на плоскость (x, y).

Рисунок-4.8. Пример маршрутизации в 3-слойном глобальном графе

Рисунок-4.9. Проекции деревьев

Рисунок-4.10. 5-слойная маршрутизация (плотность равна 3)

Этот же пример был решен после добавления двух слоев (удельное сопротивление слоев 4 и 5 мы уменьшили в 10 раз по сравнению со слоями 2 и 3, удельная емкость и характеристики via оставили без изменения, как на слоях 2 и 3 соответственно). Алгоритм построил решение, показанное на рис. 4.10, с плотностью маршрутизации 3. Здесь мы не учитывали плотность via-соединений, т. к. пропускные способности таких ребер в примере не ограничены. Времена прихода сигнала в основные выходы схемы 12 и 13 соизмеримы с аналогичными временами для 3-слойной маршрутизации.

Упражнение 4.1. Построить МДШ в графе, изображенном на рис. 4.7a, для случая евклидовой метрики.

Упражнение 4.2. Построить МДШ в графе, изображенном на рис. 4.7a, в котором длины путей из левого нижнего терминала минимальны (для случая евклидовой метрики).

Упражнение 4.3. Построить МДШ в графе, изображенном на рис. 4.7a, в котором длины путей из левого нижнего терминала минимальны (для случая прямоугольной метрики).

ЗАДАЧА КОММИВОЯЖЕРА

В задаче коммивояжера задана матрица попарных расстояний между городами. Требуется найти такой порядок посещения городов, чтобы пройденное расстояние было минимальным, каждый город посещался ровно один раз, и коммивояжер вернулся в тот город, с которого начал свой маршрут. Другими словами, во взвешенном полном неориентированном графе требуется найти гамильтонов цикл минимального веса. Если граф ориентированный и вес прямой дуги может не совпадать с весом обратной дуги, то требуется найти гамильтонов контур минимального веса.

Задача коммивояжера занимает особое место в комбинаторной оптимизации и исследовании операций. Исторически она была одной из тех задач, которые послужили толчком для развития этих направлений. Простота формулировки, конечность множества допустимых решений, наглядность и в тоже время колоссальные затраты на полный перебор до сих пор подталкивают математиков к разработке все новых и новых численных методов. Фактически, все свежие идеи сначала тестируются на этой задаче. С точки зрения приложений она не представляет интерес. Куда важнее ее обобщения для задач транспортировки грузов и логистики, когда несколько транспортных средств ограниченной грузоподъемности должны обслуживать клиентов, посещая их в заданные временные окна. В классической задаче коммивояжера все детали реальных приложений отсутствуют. Оставлена только комбинаторная суть, чисто математическая проблема, с которой не удается справиться уже полвека. Именно этой широко известной задаче посвящена данная глава.

Вычислительная сложность

Известно, что задача о гамильтоновости графа является NP-полной. В задаче коммивояжера требуется найти гамильтонов цикл минимальной длины. Это не задача распознавания. Она не лежит в классе NP, но она не проще проверки гамильтоновости графа. Действительно, если существует точный полиномиальный алгоритм для задачи коммивояжера, то можно легко построить точный полиномиальный алгоритм и для проверки гамильтоновости графа. Для этого достаточно по графу , чью гамильтоновость мы исследуем, построить матрицу расстояний 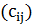задачи коммивояжера по следующему правилу: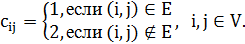

Если на решении задачи коммивояжера функционал равен 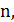то граф является гамильтоновым. Обратное тоже верно. Задачи вне класса NP, которые не проще NP-полных задач, называют NP-трудными. Задача коммивояжера принадлежит этому классу. Фактически мы получили доказательство даже более сильного утверждения.

Теорема 5.1. Задача коммивояжера является NP-трудной, даже когда матрица 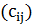является симметричной и состоит из 1 и 2.

Легко проверить, что неравенство треугольника 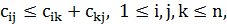в этом случае также выполняется. Говорят, что задача является NP-трудной в сильном смысле, если она остается NP-трудной даже при унарной кодировке исходных данных. При двоичной кодировке целое число требует 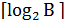ячеек памяти. При унарной кодировке требуется 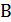ячеек памяти. Переход к унарной кодировке влечет рост требуемой памяти и, как следствие, рост длины записи исходных данных. Грубо говоря, задача является NP-трудной в сильном смысле, если она остается NP-трудной, когда все числа в исходных данных ограничены некоторой константой.
Из приведенного выше доказательства следует, что задача коммивояжера является NP-трудной в сильном смысле.

Полученное утверждение говорит о том, что точный полиномиальный алгоритм для задачи коммивояжера построить, скорее всего, не удастся. По-видимому, таких просто не существует. Следовательно, надо либо выйти за рамки полиномиальных алгоритмов, либо искать приближенные решения задачи. Следующая теорема говорит о том, что второй подход может оказаться не проще точного решения задачи. Пусть для примера 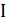задачи коммивояжера величина 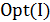задает длину кратчайшего гамильтонова цикла, а некоторый алгоритм 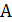на этом примере дает ответ .

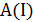Теорема 5.2. Если существует приближенный полиномиальный алгоритм 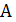и такая положительная константа 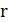, что для любого примера 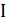задачи коммивояжера справедливо неравенство

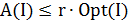, то классы P и NP совпадают.

Доказательство. Рассмотрим снова задачу о гамильтоновом цикле и построим матрицу 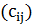по следующему правилу: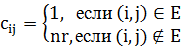

Применим приближенный алгоритм Если 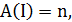то граф содержит гамильтонов цикл.

Предположим, что 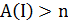. Тогда 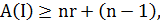так как путь коммивояжера проходит как минимум через одно «тяжелое» ребро. Но в этом случае граф не может иметь гамильтонов цикл, так как алгоритм ошибается не более чем в 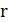раз. Следовательно, полиномиальный алгоритм 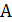дает правильный ответ для NP-полной задачи и P = NP. ∎

Из доказательства теоремы следует, что константу 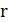можно заменить на любую, например, экспоненциально растущую функцию от 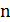. Повторяя рассуждения, получаем, что относительная точность полиномиальных алгоритмов в худшем случае не может быть ограничена, в частности, величиной 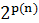, где 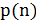– произвольный полином от размерности задачи, если P ≠ NP.

Заметим, что, в отличие от доказательства теоремы 5.1, новая конструкция уже не гарантирует выполнение неравенства треугольника. Это наводит на мысль, что при дополнительных ограничениях на матрицу 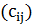можно получить полиномиальные алгоритмы с гарантированной точностью. Это действительно так, и ниже будут представлены такие алгоритмы для матриц, удовлетворяющих неравенству треугольника. Подробный обзор таких алгоритмов можно найти, например, в [14].

Рассмотрим теперь другой класс алгоритмов – итерационные алгоритмы локального улучшения. Каждая итерация будет иметь полиномиальную трудоемкость, но число итераций может оказаться в худшем случае экспоненциальной величиной. Пусть 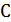– гамильтонов цикл, а 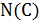– окрестность цикла 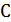, то есть все циклы, которые можно получить из цикла 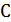некоторой локальной перестройкой. Например, 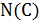– окрестность 2-замена: выбираем в 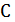два несмежных ребра и меняем их на два других, чтобы снова получить гамильтонов цикл (рис. 5.1).

a

b

c

d

a

b

c

d

Рис. 5.1. Окрестность 2-замена

Мощность такой окрестности – 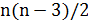. Аналогично можно получить окрестность 3-замена, 4-замена и т. д.

Конструктивные алгоритмы

Конструктивными алгоритмами принято называть такие алгорит