Проверка качества линейных регрессионных моделей

БЛОК 1

1. Проблема неэффективности регрессионных оценок может привести к ­­­­­­­­­­­­­­­­___­­ стандартных ошибок.

○ смещению,

○ занижению,

○ неидентифицируемости,

○ завышению.

2. Средняя ошибка аппроксимации служит для …

○ определения среднего значения расчетных значений зависимой переменной,

○ оценки параметров регрессии,

○ оценки качества модели,

○ расчета средних ошибок параметров регрессии.

3. В парной линейной регрессии остаточная дисперсия равна 2. Количество наблюдений равно 10. Число степеней свободы равно 8. Тогда сумма квадратов остатков равна …

○ 4,

○ 18,

○ 16,

○ 20.

4. Теорема Гаусса-Маркова имеет следующую формулировку.

○ при выполнении всех условий Гаусса-Маркова оценки коэффициентов регрессии, построенной обычным методом наименьших квадратов, будут эффективными, линейными, несмещенными оценками,

○ при выполнении 4-х условий Гаусса-Маркова оценки коэффициентов регрессии, построенной обычным методом наименьших квадратов, будут значимо отличаться от нуля,

○ при выполнении хотя бы одного из условий Гаусса-Маркова оценки коэффициентов регрессии, построенной обычным методом наименьших квадратов, будут неэффективными, линейными, смещенными оценками,

○ при выполнении 4-х условий Гаусса-Маркова оценки коэффициентов регрессии, построенной обычным методом наименьших квадратов, будут неэффективными, нелинейными, несмещенными оценками.

5. В случае нормального распределения остатков линейной регрессионной модели 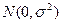оценки параметров регрессии, полученные методом наименьших квадратов, …

○ равны между собой,

○ равны нулю,

○ распределены по закону Стьюдента,

○ имеют нормальное распределение.

6. При помощи коэффициента детерминации оценивается …

○ качество подгонки регрессионной модели к наблюдаемым значениям результирующего признака,

○ существенность оценок параметров регрессии,

○ статистическая значимость результативного признака,

○ неоднородность выборочных данных.

7. При применении метода наименьших квадратов свойствами эффективности, состоятельности и несмещенности обладают оценки …

○ случайной величины,

○ зависимой переменной,

○ параметров,

○ независимой переменной.

8. Обобщенный МНК применяется в случае…

○ наличия в остатках гетероскедастичности или автокорреляции,

○ наличия в модели мультиколлинеарности,

○ наличия в модели фиктивных переменных,

○ наличия в модели незначимых оценок.

9. По уравнению регрессии 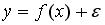рассчитано значение коэффициента корреляции, которое характеризует тесноту связи между …

○ y и e,

○ y и f(x),

○ y и х,

○ x и e.

10. Определение дисперсии на одну степень свободы приводит общую, объясненную и остаточную дисперсии к…

○ одной размерности,

○ безразмерному виду,

○ сравнимому виду,

○ табличному виду.

11. Относительные отклонения расчётных значений результирующего признака от его наблюдаемых значений используются при расчёте …

○ t-критерия Стьюдента

○ коэффициента эластичности

○ параметров регрессии

○ средней ошибки аппроксимации

12. Формула расчета коэффициента детерминации имеет вид …

○

○

○

○

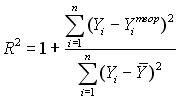
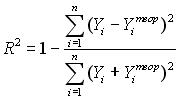
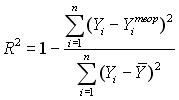
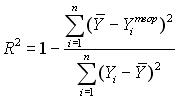
13. Пусть исследуется линейная зависимость вида 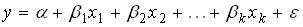. Величина, показывающая, на сколько процентов изменится 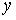при изменении 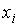на 1%, называется

○ коэффициентом регрессии

○ коэффициентом корреляции

○ коэффициентом эластичности

○ коэффициентом детерминации.

14. Коэффициент детерминации рассчитывается для оценки качества…

○ параметров уравнения регрессии

○ мультиколлинеарных факторов

○ факторов, не включенных в уравнение регрессии

○ подбора уравнения регрессии.

15. По расположению точек корреляционного поля (диаграммы рассеяния) далеко не всегда можно принять окончательное решение о виде уравнения регрессии. Если теоретические соображения или опыт предыдущих исследований не могут подсказать точного решения, то необходимо сделать расчеты по нескольким уравнениям. Предпочтение отдается уравнению, для которого минимальна величина _____ дисперсии

○ остаточной

○ объясненной

○ общей

○ факторной.

16. Тест Годлфельда-Квандта, используемый для обнаружения гетероскедастичности, основан на …

○ предположении пропорциональности между дисперсией остатков и независимой переменной с коэффициентом ,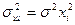

○ сравнении рангов значений независимой переменной 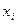и остатков модели ,

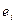○ минимизации остатков ,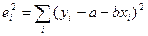

○ сравнении рангов значений зависимой переменной 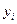и остатков модели .

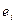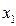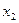17. Пусть рассматриваются две случайные величины и . Для них вычислены коэффициент парной линейной регрессии r и корреляционное отношение по уравнению связи 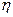. Известно, что 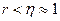. Это означает, что …

○ зависимость между 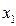и 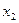строго линейная,

○ имеется функциональная нелинейная зависимость между 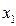и ,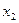

○ не существует функциональной зависимости между 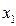и ,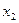

○ имеется слабая нелинейная зависимость между 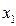и .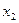

18. На рисунке отражены результаты теста Дарбина-Уотсона

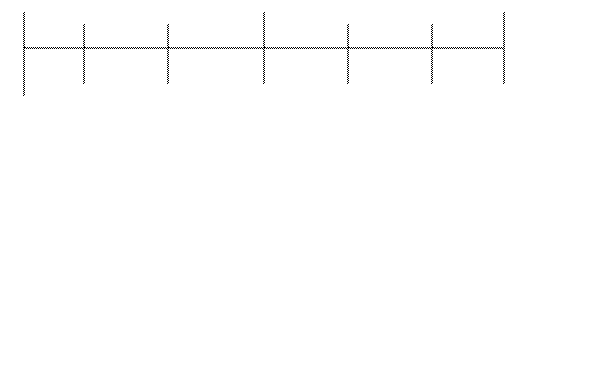
где 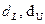– соответственно нижняя и верхняя границы для критического значения, а DW – наблюдаемое значение критерии Дарбина-Уотсона ( 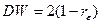, где 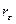– коэффициент автокорреляции остатков). Можно сделать вывод, что …

○ в остатках регрессионной модели присутствует положительная автокорреляция,

○ нельзя ни отклонить, ни принять нулевую гипотезу об отсутствии автокорреляции в остатках регрессионной модели (зона неопределенности),

○ в остатках регрессионной модели присутствует отрицательная автокорреляция,

○ нет оснований отвергнуть нулевую гипотезу об отсутствии автокорреляции в остатках регрессионной модели (автокорреляция в остатках отсутствует).

19. Коэффициент детерминации представляет собой отношение …

○ необъясненной уравнением регрессии дисперсии результирующего фактора к объясненной дисперсии этого фактора,

○ объясненной уравнением регрессии дисперсии результирующего фактора к общей дисперсии этого фактора,

○ дисперсии отклонений к общей дисперсии результирующего фактора,

○ необъясненной уравнением регрессии дисперсии результирующего фактора к общей дисперсии этого фактора.

20. Автокорреляцию в остатках модели линейной регрессии можно обнаружить с помощью …

○ критерия Дарбина-Уотсона,

○ критерия Спирмена,

○ критерия Фишера,

○ критерия Гольдфельда-Квандта.

21. Коэффициент детерминации может принимать значения в интервале …

○ от -1 до 1,

○ от 0 до 1,

○ от 0 до 100,

○ от -1 до 0.

БЛОК 2

1. Если предпосылки МНК не выполняются, то остатки могут …

□ иметь нулевую среднюю величину,

□ характеризоваться отсутствием автокорреляции,

□ быть гетероскедастичными,

□ не подчиняться закону нормального распределения.

2. Укажите условия, которые выполняются, если оценки параметров уравнения регрессии обладают свойствами состоятельности, эффективности и несмещенности.

□ равенство нулю математического ожидания остатков,

□ максимальная дисперсия остатков,

□ зависимость математического ожидания остатков от величины выборки,

□ наименьшая дисперсия остатков.

3. Пусть в модели 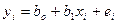случайные отклонения 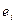гетероскедастичны. При этом обнаружено, что дисперсия 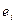пропорциональна значениям 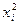. Укажите последовательность этапов одного из методов устранения гетероскедастичности.

1. □ выдвигается гипотеза, что дисперсии отклонений пропорциональны значениям 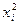. Вводится коэффициент пропорциональности ,

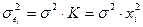4. □ оценивается общее качество преобразованной модели,

2. □ строится регрессия новой зависимой переменной 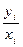на новую независимую переменную ,

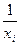3. □ оцениваются коэффициенты новой регрессии и их статистическая значимость.

4. При выполнении предпосылок метода наименьших квадратов (МНК) остатки уравнения регрессии, как правило, характеризуются …

□ случайным характером,

□ высокой степенью автокорреляции,

□ гетероскедастичностью,

□ нулевой средней величиной.

5. Для уравнения зависимости предложения на некоторый товар от цены за единицу товара получено значение коэффициента детерминации, равное 0,64. Следовательно, …

□ отношение факторной дисперсии предложения к его общей дисперсии равно 0,64,

□ отношение факторной дисперсии предложения к его общей дисперсии равно 0,8,

□ отношение остаточной дисперсии предложения к его общей дисперсии равно 0,36,

□ отношение остаточной дисперсии предложения к его общей дисперсии равно 0,6.

6. Предпосылками метода наименьших квадратов (МНК) являются …

□ отсутствие автокорреляции в остатках,

□ гомоскедастичность остатков,

□ функциональная связь между зависимой и независимой переменными,

□ присутствие в эконометрической модели более чем двух факторов.

7. Если оценки параметров уравнения регрессии обладают свойствами состоятельности, эффективности и несмещенности, то …

□ возможен переход от точечного оценивания к интервальному,

□ предпосылки метода наименьших квадратов не выполняются,

□ при большом числе выборочных оцениваний остатки не будут накапливаться,

□ точность модели снижается с увеличением объема выборки.

8. Укажите последовательность этапов обнаружения авткорреляции остатков по критерию Дарбина-Уотсона.

3. □ расчет статистики Дарбина-Уотсона,

2. □ оценка отклонений фактических значений объясняемой переменной от ее расчетных значений,

4. □ оценка значимости автокорреляции,

1. □ построение уравнения регрессии.

9. Разность 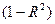, где 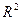– коэффициент детерминации …

□ оценивает значимость каждого из факторов, включенных в уравнение регрессии,

□ является показателем тесноты связи между двумя переменными,

□ характеризует долю дисперсии остаточной величины в общей дисперсии зависимой переменной у,

□ может рассчитываться для оценки качества подбора уравнения регрессии.

10. Практическая значимость свойств несмещенности, эффективности и состоятельности оценок параметров, полученных при помощи метода наименьших квадратов выражается в …

□ накоплении значений остатков при большом числе выборочных оцениваний,

□ отсутствии накопления остатков при большом числе выборочных оцениваний,

□ уменьшение точности с увеличением объема выборки,

□ возможности перехода от точечного оценивания к интервальному.

11. Если оценки параметров уравнения регрессии обладают свойствами состоятельности, эффективности и несмещенности, то …

□ математическое ожидание остатков равно нулю и они характеризуются минимальной дисперсией,

□ наблюдается уменьшение точности оценивания параметров с увеличением объема выборки,

□ происходит накапливание значений остатков при большом числе выборочных оцениваний,

□ возможен переход от точечного оценивания к интервальному.

12. Обобщенный МНК подразумевает …

□ введение в выражение для дисперсии остатков коэффициента пропорциональности,

□ переход от множественной регрессии к парной,

□ двухэтапное применение метода наименьших квадратов,

□ преобразование переменных.

13.Значение коэффициента детерминации составило 0,9, следовательно отношение ______ дисперсии к общей дисперсии равно _____.

□ факторной … 0,9,

□ остаточной … 0,1,

□ остаточной … 0,9,

□ факторной … 0,1.

14. Укажите верные характеристики коэффициента эластичности:

□ коэффициент эластичности показывает на сколько изменится значение результирующего фактора при изменении объясняющего фактора на одну единицу

□ по значению коэффициента эластичности можно судить о силе связи объясняющего фактора с результирующим

□ коэффициент эластичности показывает на сколько процентов изменится значение результирующего фактора при изменении на один процент объясняющего фактора

□ коэффициент эластичности является постоянной величиной для всех видов моделей.

15. Предпосылками метода наименьших квадратов (МНК) являются …

□ отсутствие автокорреляции в остатках

□ функциональная связь между зависимой и независимой переменными

□ присутствие в эконометрической модели более чем двух факторов

□ гомоскедастичность остатков.

16. Проверку выполнения предпосылки МНК (метода наименьших квадратов) о гомоскедастичности (гетероскедастичености) остатков можно провести…

□ на основании параметрических тестов

□ дифференцированием переменных

□ методом линеаризации уравнения

□ визуально по графику.

17. Если предпосылки метода наименьших квадратов не выполняются, то оценки параметров уравнения регрессии могут не обладать свойствами …

□ состоятельности

□ правильности

□ несмещенности

□ эффективности.

18. Укажите последовательность этапов проведения теста Голдфелда-Квандта для парной линейной регрессии

1. □ упорядочение наблюдений по возрастанию значений объясняющей переменной

3. □ оценка сумм квадратов отклонений для регрессий по k-первым и k-последним наблюдений

4. □ вычисление статистики Фишера

2. □ оценка регрессий для k-первых и k-последних наблюдений.

19. Величина коэффициента детерминации …

□ оценивает значимость каждого из факторов, включенных в уравнение регрессии

□ рассчитывается для оценки качества

□ характеризует долю дисперсии

□ характеризует долю дисперсии зависимой переменной y, объясненную уравнением, в ее общей дисперсии.

20. Несмещенность оценки характеризуется …

□ равенством нулю математического ожидания остатков

□ отсутствием накопления остатков при большом числе выборочных оцениваний

□ максимальной дисперсией остатков

□ зависимостью от объема выборки значения математического ожидания остатков.

21. Обобщенный метод наименьших квадратов может применяться в случае нарушения предпосылки МНК о _______ остатков.

□ отсутствии автокорреляции

□ максимизации суммы квадратов

□ гомоскедастичности

□ существовании.

22. Проявление гетероскедастичности в остатках удается устранить при помощи обобщенного метода наименьших квадратов путем …

□ расчета критерия Дарбина-Уотсона гомоскедастичных остатков,

□ введения в модель фиктивных переменных,

□ ведение в выражение для дисперсии остатков коэффициента пропорциональности,

□ преобразования переменных.

23. Если оценка параметра эффективна, то это означает …

□ уменьшение точности с увеличением объема выборки,

□ возможность перехода от точечного оценивания к интервальному,

□ наименьшую дисперсию остатков,

□ невозможность перехода от точечного оценивания к интервальному.

24. Обобщенный метод наименьших квадратов может использоваться для корректировки ……………… остатков.

□ стандартной ошибки,

□ доверительного интервала,

□ автокорреляции,

□ гетероскедастичности.