Спекание с участием жидкой фазы

Взаимное припекание твердых тел может происходить в условиях, когда в месте контакта между ними появляется жидкая фаза. Жидкая фаза может появиться при температуре равной или более высокой, чем температура плавления легкоплавкого компонента, или же вследствие так называемого «контактного» плавления, которое происходит при температуре более низкой, чем температура плавления легкоплавкого компонента.

Важнейшим для проблемы спекания является случай, когда объем легкоплавкого вещества мал по сравнению с объемом тугоплавкого вещества. В этом случае в контактной области между одноименными тугоплавкими частицами появляется прослойка расплава, в котором тугоплавкое вещество может быть частично или полностью растворимо.

Кинетика припекания, вне зависимости от механизма появления жидкой фазы, зависит от закономерностей распространения жидкости по поверхности сфер. Принципиально в отсутствие внешних сил, в частности силы тяжести, возможны два различных механизма распространения жидкости на твердой поверхности: поверхностная диффузия (миграция) и полное смачивание. В случае, когда определяющим является механизм поверхностной диффузии, атомы (ионы) из жидкой капли распространяются на твердой поверхности, подчиняясь закону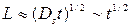. В реальных условиях спекания более существенным является механизм смачивания.

Под полным смачиванием условно следует понимать вязкое течение, обусловленное лишь уменьшением поверхностной энергии системы и не связанное с действием сил тяжести. В случае идеально гладкой поверхности твердого тела полное смачивание возможно, если:

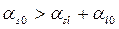, (8.1)

где α_s0, α_sl и α_l0 – соответственно поверхностные энергии твердого тела на границе с вакуумом, твердого тела на границе с жидкостью и жидкости на границе с вакуумом*).

Каждая твердая поверхность отнюдь не идеально гладкая; она обладает микрорельефом, который влияет и на условия, при которых растекание становится возможным, и на кинетику растекания.

Следует различать краевой угол θ₀, полученный в измерениях, при которых остается незаметным микрорельеф поверхности, и краевой угол θ, который обнаруживается в тонких измерениях, учитывающих микрорельеф смачиваемой поверхности. Отличие между величинами θ и θ₀ определяется величиной шероховатости поверхности**) K, являющейся отношением площади истинной поверхности к той, которая была бы при идеальной гладкости.

Установлена связь между величинами θ, θ₀ и K в виде:

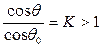. (8.2)

Из (8.2) следует, что если шероховатость настолько велика, что

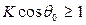, (8.3)

то жидкость будет абсолютно смачивать шероховатую поверхность и в том случае, если бы на гладкой поверхности смачивания не имело места.

Представляет интерес задача о кинетике полного смачивания. Временная зависимость радиуса растекающейся r может быть определена, если приравнять силу F₁, растягивающую каплю, к силе вязкого сопротивления F₂:

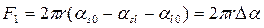. (8.4)

Величину F₂ можно приближенно оценить, считая, что растекающаяся капля массы т в любой момент времени имеет форму цилиндра высотой h(t) и радиуса r(t). В предположении, что растекание капли осуществляется в режиме ньютоновского течения с постоянным по толщине слоя градиентом скорости, сила F₂ определится уравнением

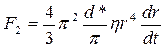, (8.5)

где d* и η – соответственно плотность и вязкость вещества капли. Приравнивая (8.4) и (8.5), после интегрирования получаем:

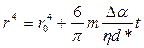. (8.6)

Таким образом, в случае, когда распространение капли на поверхности происходит вследствие полного смачивания, прирост радиуса зависит от ее массы.

Как уже указывалось, жидкая фаза в месте контакта разнородных твердых частиц может появиться вследствие «контактного» плавления. Эффект «контактного» плавления является естественным следствием стремления системы к уменьшению свободной поверхностной энергии и наблюдается, когда между поверхностной энергией на границе соприкосновения твердых тел α_AB и поверхностными энергиями на границах «твердые вещества – расплав, появившийся в месте контакта» (α_Al, α_Bl), имеет место неравенство:

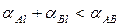. (8.7)

Выполнимость этого неравенства зависит от констант, определяющих диаграмму равновесия соответствующей системы. Оно, в частности, должно выполняться в системах, описываемых диаграммами эвтектического типа и с точкой равных концентраций в минимуме. Как это следует из расчетов, в системах, где наблюдается «контактное» плавление, одновременно с неравенством (8.7) выполняются и следующие неравенства:

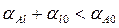, (8.8)

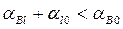, (8.9)

которые означают, что расплав, появляющийся в месте контакта твердых частиц, смачивает эти частицы или растекается по их поверхности.

Экспериментально «контактное» плавление наблюдается на большом количестве металлических и неметаллических систем.
Установлены следующие особенности процесса:

1. Появление жидкости прекращается в момент нарушения контакта между частицами пары.

2. Жидкий расплав из приконтактной области растекается по поверхности твердых частиц.

3. В приконтактной области твердые крупинки частично растворяются в жидком расплаве в соответствии с диаграммами состояния.

4. В изотермических условиях скорость увеличения толщины жидкой прослойки между образцами контактной пары, если отвод жидкости отсутствует, описывается законом

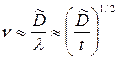, (8.10)

где 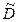— эффективный коэффициент диффузии в расплаве,

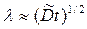— ширина жидкой прослойки.

5. Если твердые частицы содержат трещины, жидкий расплав проникает в них. Трещины при этом расширяются за счет расклинивающего действия жидкости.

Имея в виду описанные особенности «контактного» плавления, процесс взаимного припекания двух частиц можно схематически изобразить так, как это сделано на рис. 8.1. На заключительной стадии процесса припекания жидкая фаза будет отсутствовать, если соотношение между начальными массами твердых частиц таково, что, в соответствии с диаграммой состояния, при полном взаимном растворении может образоваться раствор концентрации меньшей, чем предельная при температуре опыта.

Важным для проблемы спекания является случай, когда между двумя одноименными частицами А расположена прослойка расплава В, в котором частично или полностью растворимо вещество твердых частиц.

Наличие жидкой манжеты между двумя твердыми частицами обусловливает возникновение сил, стягивающих частицы и таким образом влияющих на кинетику спекания.

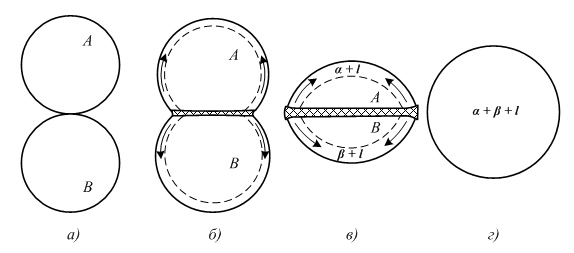
Рис. 8.1. Схематическое изображение этапов припекания крупинок из веществ А и В, в месте контакта которых возникает жидкая фаза, α и β – твердые растворы на основе A и В;
l – жидкая фаза

Рассмотрим задачу о взаимодействии двух крупинок, между которыми защемлена жидкость (рис. 8.2). Результирующая сила взаимодействия между двумя крупинками состоит из двух слагаемых. Одно из них обусловлено наличием искривленной поверхности жидкости и составляет:

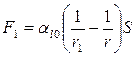, (8.11)

где S – проекция площади границы «жидкость – твердое тело» на плоскость, перпендикулярную к направлению действующей силы.

Второе слагаемое (F₂) обусловлено стремлением свободной поверхности жидкости к сокращению и не зависит от ее кривизны. Оценить эту силу можно, спроектировав силу поверхностного натяжения, действующую по периметру

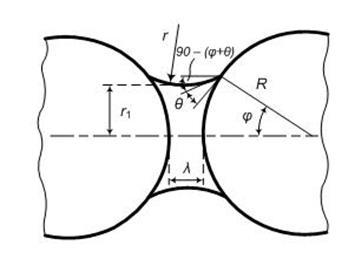
Рис. 8.2. Схема контакта двух сферических крупинок, разделенных жидкой прослойкой.
q – краевой угол смачивания

соприкосновения жидкости и твердой частицы, на прямую, соединяющую центры твердых частиц:

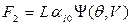, (8.12)

где L – длина периметра смачивания,

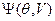– функция, зависящая от краевого угла смачивания θ, объема защемленной жидкости V и геометрии крупинок.

В частном случае двух сферических частиц с радиусом R (рис. 8.2):

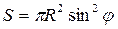, (8.13)

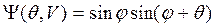(8.14)

Итак,

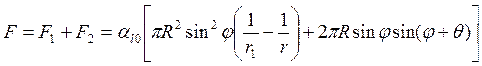, (8.15)

где

,

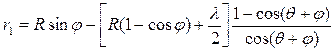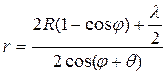. (8.16)

В (8.16) λ – величина зазора между частицами.

Формулы (8.15) и (8.16) справедливы в случае, когда искажающим влиянием силы тяжести на форму мениска жидкости можно пренебречь, т.е. либо в случае крупных частиц при малых количествах жидкости (малые значения φ на рис. 8.2), либо при любых значениях φ для частиц малого размера.

Из (8.15) следует, что при некотором критическом значении угла смачивания θ*, зависящем от количества жидкости между сферическими крупинками,

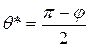, (8.17)

сила, стягивающая частицы, обращается в ноль и при дальнейшем увеличении количества жидкости появится сила, отталкивающая частицы. В последнем случае наличие жидкой фазы будет препятствовать процессам, приводящим к взаимному припеканию частиц (см. далее).

Представляет интерес зависимость силы F от величины зазора λ между частицами. В соответствии с (8.15) эта зависимость будет различной при различных значениях φ и θ.

Экспериментально величина капиллярной силы, действующей между твердыми частицами с прослойкой жидкости в области контакта, изучена с использованием устройства (рис. 8.2), с помощью которого сила F могла быть измерена с большой точностью путем определения расстояния между ползунами 3 и 4 в момент разъединения шариков 1, висящих на гибких нитях 2.

Варьировались пары «жидкость – вещество шариков», радиусы шариков и количество жидкости, защемленной между шариками. В качестве жидкой фазы использовались вазелиновое вакуумное масло, бензиловый и этиловый спирты, краевой угол которых по отношению к стали (материал шариков) близок к нулю. Результаты измерений F, выполненных с различными веществами и шариками разных размеров, показаны на рис. 8.3. Сплошной линией проведена расчетная кривая, ход которой в избранных координатах не зависит от α и R. Расчетная кривая удовлетворительно согласуется с результатами измерений.

Соотношение (8.15) вполне удовлетворительно описывает экспериментальные данные и в случае, когда θ ≠ 0. Измерена сила притягивания стальных шариков, разделенных прослойкой глицерина (θ ≈ 55°). Экспериментально найденные

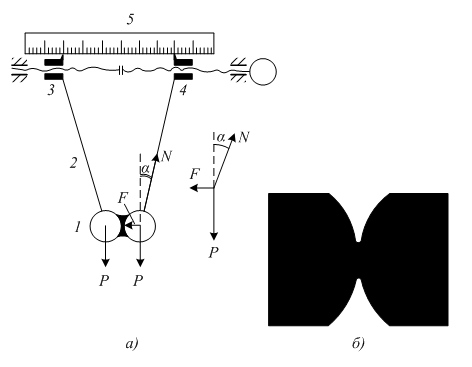
Рис. 8.3. а – схема устройства для измерения капиллярной силы, обусловленной жидкой прослойкой между твердыми крупинками; б – фотография контакта между металлическими сферами, разделенными жидкой прослойкой

значения F с погрешностью в несколько процентов совпадают с расчетом по (8.15).

Аналогичная ситуация наблюдается и для систем тугоплавких неметаллических материалов. При этом особое внимание в последние годы уделяется добавкам эвтектического состава, образующим жидкую фазу в обжиге. Такие составы в силу минимальных температур плавления, наличия структурированных элементов в жидкости, несущих «генетическую» память о кристаллических фазах эвтектики, упорядоченного мелкокристаллического строения весьма перспективны с точки зрения управления процессом формирования структуры керамического материала в ходе высокотемпературной термообработки. Следовательно, массоперенос при спекании материала можно регулировать посредством оптимизации состава, структуры и свойств жидкой фазы. В первую очередь модифицирующий компонент влияет на процесс растворения – кристаллизации, являющийся основным при жидкофазном спекании.

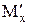Установлено, что структурированные жидкости эвтектических составов (СЭЖ), образующиеся в процессе обжига. Такие жидкости должны принадлежать к системам типа , где – катион металла оксида, являющегося в стеклообразующих системах модификатором, 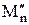– катион оксида, являющегося в стеклообразующих системах сеткообразователем.

Рассмотрим принципы, положенные в основу выбора подобных модифицирующих компонентов. С этой точки зрения наиболее важными параметрами эвтектической жидкости являются ее кислотно-основные свойства, а также температура плавления, параметры смачивания и вязкостные характеристики.

Согласно электронно-координационной теории, кислотой считается вещество, которое может принять электрону пару с образованием координационной связи. В расплавах тугоплавких неметаллических соединений носителем электронной пары является ион O^2-, а следовательно оксид, способный образовывать сложные катионно - кислородные комплексы, будет обладать кислыми свойствами. Мерой кислотности может служить отношение энергии связи элемента с кислородом к координационному числу (к.ч.) катиона. Сопоставление этих величин позволяет заключить, что кислотные свойства оксидов убывают в ряду:

B₂O₃ (к.ч.=3) > P₂O₅ > V₂O₅ > GeO₂ > SiO₂ > B₂O₃ (к.ч.=4) > ZrO₂ (к.ч.=6) > TiO₂= PbO (к.ч.=2)

Наиболее перспективно в технологии оксидной керамики использование оксидов кремния, циркония и титана.

Таким образом, для эффективного протекания процесса растворения – кристаллизации расплав должен обладать кислыми свойствами. Последнее продиктовано тем, что ион Al³⁺ изменяет свою координацию в зависимости от кислотности расплава. В основных средах он четырехкоординирован и представлен комплексами AlO 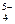, в кислых – шестикоординирован и представлен группами AlO 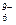. Энергетический барьер при переходе иона Al³⁺ в кислый расплав будет значительно ниже, нежели в основной.

Оценка кислотно-основных свойств расплава может быть проведена по методу А.А. Аппена. Мерой координационного состояния иона алюминия, а следовательно, и кислотности расплава в этом случае является параметр y_Al, который рассчитывается по следующему выражению:

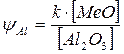, (8.18)

где [MeO] – молярная доля оксида, способного влиять на координационное состояние иона алюминия – т.н. активного оксида;

[Al₂O₃] – молярная доля оксида алюминия в расплаве.

Относительно значения величины k однозначного суждения не существует. Аппеном указывается, что наиболее активными являются ионы с низким зарядом и высоким радиусом, например Na⁺, K⁺, Ba²⁺. В этом случае k = 1; эти ионы приводят к снижению к.ч. Al³⁺ по сравнению с корундом (к.ч. = 6) до 4. Менее активны ионы Li⁺, Ca²⁺. Значение k в этом случае не приводится. Ионы малого радиуса, например Fe²⁺, Mg²⁺, не способны изменять координацию катиона алюминия в расплаве по сравнению с корундом. Отсюда следует, что соотношение (8.18) также четко не определено.

Для оценки кислотно-основных свойств расплавов поэтому удобнее пользоваться фактором B, представляющим собой соотношение мольных долей основных 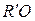и 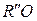оксидов в расплаве. Так, например, исходя из того, что CaO наиболее сильно повышает основность, а SiO₂ – кислотность расплавов, для ориентировочной оценки мерой основности расплава используют соотношение

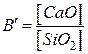, (8.19)

где [CaO] и [SiO₂] – молярные доли компонентов в расплаве.

Принято считать, что при B¢ £ 0,54 расплавы являются кислыми, а при
B¢ ³ 2,235 – основными. Нейтральные расплавы имеют промежуточное значение параметра B¢, при его увеличении от 0,54 до 1,3 кислотность постепенно сменяется нейтральностью, а от 1,3 до 2,235 – основностью.

Подбор оксида модификатора осуществляют исходя из величины энергии связи катион модификатор – кислород, оцениваемой по значению ионного потенциала катиона, равного отношению его условного заряда к радиусу. Показано, что наилучшими свойствами характеризуется керамика, содержащая СЭЖ, ионный потенциал модификаторов для которых составляет 20 – 30 нм ^{- 1} (табл. 8.1).

При низких значениях энергии связи катион-модификатор способен отдавать ионы кислорода из своего окружения иону алюминия, понижая тем самым координационное число последнего до 4. В случае высоких энергий связи, т.е. для

Таблица 8.1