Геометрические характеристики контактного перешейка

Геометрическая характеристика	Сферы	Цилиндры
Центры не сближаются	Центры сближаются	Центры не сближаются	Центры сближаются
R	x2/2R0	x2/4R0	x2/2R0	х2/4R0
S	2πx3/R0	πx3/R0	2x2/R0	х2/R0
V	πx4/2R0	πx4/4R0	x3/R0	х3/R0

В начальный момент контакт между сферами, строго говоря, не является точечным. Под влиянием собственной массы сферы упруго деформируются и приходят в контакт по площади круга радиусом x₀ и h₀. Известно, что:

, (1.2)

где F – сила, сжимающая шары, радиусы которых R₁ и R₂;

(1.3)

В случае шаров равного размера (R₁ = R₂ = R₀) из одного вещества исходя из (1.2) и (1.3) следует:

; . (1.4)

В (1.4) учтено, что . Найденные экспериментально значения x₀ и h₀ находятся за пределами точности экспериментальных работ по припеканию.

Таким образом, упругой деформацией в зоне контакта можно пренебречь, если припекание осуществляется “свободно”, т.е. в отсутствие прижимающих усилий.

Термодинамическая целесообразность переноса вещества в область контактного перешейка обусловлена тем, что происходящее при этом перемещение поверхности перешейка сопровождается уменьшением общей поверхности и, следовательно, поверхностной энергии системы. Перемещение поверхности перешейка осуществляется под влиянием лапласовского давления:

(1.5)

В рассматриваемом случае поверхностью между фазами является поверхность перешейка, геометрия которой характеризуется двумя радиусами кривизны: r и x.

Механизм вязкого течения

Конкретный механизм переноса массы вследствие течения существенно зависит от структуры вещества частиц. В случае аморфного вещества вязкое течение осуществляется путем кооперативного перемещения атомов или ионов, и коэффициент вязкости η является константой вещества, определяющей скорость течения. Для кристаллических тел вязкое течение вещества может осуществляться вследствие диффузионно-вязкого преобразования формы или вследствие диффузионного восхождения дислокаций. Как и в случае аморфных тел, этот процесс непороговый (предел текучести равен нулю), однако перемещение атомов (ионов) не является процессом кооперативным, а есть следствие независимых элементарных актов диффузионного перемещения под влиянием давления, приложенного извне, которое при «свободном» спекании обусловлено кривизной поверхности приконтактного перешейка.

Вне зависимости от конкретного механизма, вязкое течение вещества в область приконтактного перешейка сопровождается и увеличением площади контакта, и сближением центров контактирующих сфер (см. соотношение 1.4).

Задачу о кинетике припекания сферических крупинок вследствие вязкого течения вещества изложим, следуя следующей логике. Будем предполагать, что на протяжении всего процесса течения вещества в область приконтактного перешейка частицы сохраняют форму сферы R(t). При углах φ ≤ 1 (рис. 1.3) можно считать, что

R(t) ≈ R₀, x(t) ≈ R₀φ (1.6)

Свободная поверхность спекающихся сфер с изменением угла φ
изменяется по закону

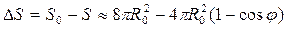(1.7)

С точностью до величин порядка φ² можно записать:

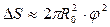, (1.8)

и соответственно работа сил поверхностного натяжения

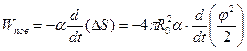. (1.9)

Для нахождения закона изменения угла φ со временем (или, что то же,
х = х(t)) работу сил поверхностного натяжения следует приравнять работе сил внутреннего трения, связанной с рассматриваемой деформацией:

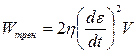, (1.10)

где – общий объем деформирующегося тела,

ε – относительная деформация тела (совокупности двух шаров).

Задача о течении вещества в область приконтактного перешейка между двумя сферическими крупинками деформация может быть охарактеризована уменьшением расстояния между центром одной из крупинок и поверхностью ее контакта с другой, так что

(1.11)

Путем математических преобразований установлено, что:

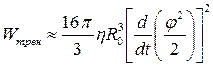(1.12)

Приравнивая (1.9) и (1.12), получим:

(1.13)

Согласно (1.6) φ ≈ x(t)/R₀, поэтому

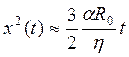(1.14)

С ростом площади контакта происходит сближение центров контактирующих сфер, расстояние между которыми l = 2(R₀ – h) определяется соотношением

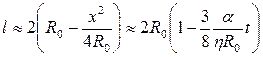(1.15)

и соответственно скорость сближения центров

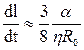. (1.16)

Характерное время t полного слияния частиц, исходный радиус которых R₀, определится соотношением *)

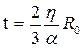, (1.17)

следующим из (1.14) в предположении x ≈ R₀.

Соотношение (1.14) экспериментально подтверждено припеканием сферических частиц стекла как к плоской стеклянной пластинке, так и между собой. Исследовано взаимное припекание сфер стекла, имевших исходный радиус 4,9∙10^{-4 см. Результаты, полученные в опытах при} T = 750 °С и 725 °С, в координатах ln (x/R₀), ln t описываются прямыми, тангенс угла наклона которых в соответствии с соотношением (1.14) равен 2.

Припекание стеклянных сфер проводили в широком интервале температур. По данным о температурной зависимости вязкости найдена энергия активации вязкого течения изучаемого сорта стекла, которая практически совпала со значением, найденным в прямых опытах.