Н. А. Макаров, Д. О. Лемешев

Н. А. Макаров, Д. О. Лемешев

ФИЗИЧЕСКАЯ ХИМИЯ

СПЕКАНИЯ

Москва

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

Российский химико-технологический университет
имени Д. И. Менделеева

Н.А. МАКАРОВ, Д.О. ЛЕМЕШЕВ

ФИЗИЧЕСКАЯ ХИМИЯ
СПЕКАНИЯ

Утверждено

Редакционным советом университета

в качестве учебного пособия

Москва

УДК 541.1(075)

ББК 24.5:35.41я7

М 152

Рецензенты:

Доктор химических наук, заведующий кафедрой

Физической химии

ФГБОУ ВПО «Российский химико-технологический университет
имени Д. И. Менделеева»
В. Ю. Конюхов

Кандидат технических наук, профессор кафедры стекла и керамики
ФГБОУ ВПО «Владимирский государственный университет
имени Александра Григорьевича и Николая Григорьевича Столетовых»

Э.П. Сысоев

Макаров Н. А.

М 152 Физическая химия спекания: учеб. пособие / Н.А. Макаров,
Д.О. Лемешев. – М.: РХТУ им. Д. И. Менделеева, 2014. –
200 с.

ISBN 978-5-7237-1202-7

Изложены современные представления о физико-химии высокотемпературного уплотнения и упрочнения (спекания) объектов различной природы, как металлических, так и тугоплавких неметаллических. Подробно рассмотрены процессы, происходящие на индивидуальном контакте взаимно припекающихся частиц, при уменьшении объема как изолированной поры, так и ансамбля пор. Проанализирована роль дефектов строения кристаллической решетки – вакансий, дислокаций, границ между зернами в процессе спекания пористых тел. Рассмотрены особенности процесса спекания смесей порошков различных веществ в связи с возможным влиянием взаимной диффузии на кинетику процесса. Изложены закономерности спекания материалов с участием жидкой фазы различной природы. Проанализированы современные экспериментальные методы исследования кинетики процесса спекания.

Предназначено для студентов вузов, обучающихся по специальности 240304 «Химическая технология тугоплавких неметаллических и силикатных
материалов»; бакалавров, магистров и аспирантов, обучающихся и по направлениям 18.03.01, 18.04.01, 18.06.01 «Химическая технология»; 22.03.01, 22.04.01 «Материаловедение и технологии материалов»; 22.06.01 «Технологии материалов» и может быть использовано в профессиональной деятельности инженерно-техническим персоналом производств тугоплавких неметаллических материалов.

УДК 541.1(075)

ББК 24.5:35.41я7

ISBN 978-5-7237-1202-7

©

Российский химико-технологический университет им. Д. И. Менделеева, 2014

ВВЕДЕНИЕ

Предлагаемое учебное пособие является последовательным изложением теоретических представлений и экспериментальных результатов, полученных в результате исследования кинетики процессов, происходящих при формировании беспористого тела из ансамбля дисперсных частиц.

Представляемая читателю книга является учебным пособием т.н. третьего поколения и является полезной для студентов вузов, обучающихся по специальности 240304 «Химическая технология тугоплавких неметаллических и силикатных
материалов»; бакалавров, магистров и аспирантов, обучающихся и по направлениям 18.03.01, 18.04.01, 18.06.01 «Химическая технология»; 22.03.01, 22.04.01 «Материаловедение и технологии материалов»; 22.06.01 «Технологии материалов» и может быть использовано в профессиональной деятельности инженерно-техническим персоналом производств тугоплавких неметаллических материалов.

Факты и идеи, заложенные в представленном учебном пособии, впервые стали известны в середине 50-х годов 20 столетия. Попытки объяснить и математически представить процессы, происходящие при уплотнении пористых твердых тел в области высоких температур, впервые объяснены теоретически в работах
Я.И. Френкеля «О вязком течении твердых тел» и Б.Я. Пинеса «О спекании
в твердой фазе».

В первой из этих работ впервые была развита идея о том, что уплотнение пористого тела обусловлено тенденцией к уменьшению свободной поверхностной энергии системы. Во второй работе представлен диффузионный механизм залечивания замкнутой поры в кристаллическом теле. Одним из важнейших открытий этой статьи стало то, что уравнение Кельвина (Томсона), определяющее избыточное давление пара над изогнутой поверхностью жидкости, не содержит массы частиц, а, следовательно, применимо к частицам с нулевой массой, т.е.вакансиям кристаллической решетки. Именно с этой точки зрения на современном этапе развития науки рассматривается физико-химия процесса спекания.

Таким образом, современная физико-химия спекания должна именоваться теорией Френкеля – Пинеса.

Важно отметить также и то, что развитие физической химии спекания происходило одновременно во взаимосвязи с исследованиями механизмов иных высокотемпературных процессов в твердом теле. Подобные исследования развивались в связи с практически важнейшей проблемой создания жаропрочных металлов и сплавов на их основе. Поэтому впервые проблемы физической химии спекания были развиты на металлических системах, а уже в настоящее время перенесены на высокотемпературные тугоплавкие неметаллические оксидные и бескислородные материалы (карбиды, нитриды, силициды, симоны, сиалоны и др.). Следовательно, движущей силой развития физико-химии спекания явились потребности технологий металлокерамического и керамического производств.

В реальных условиях спекание порошковых композиций (которые также по ходу повествования будут названы полуфабрикатом либо заготовками) является крайне сложным физико-химическим процессом. Именно потому, что при обжиге полуфабриката одновременно протекает множество процессов, находящиеся во взаимосвязи, в научно-технической литературе встречаются различные и, зачастую, несовместимые определения термина «спекание».

Последовательность процессов, происходящих при спекании, удобно по геометрическому признаку условно подразделять на три стадии, которые зачастую четко не разделены между собой.

На первой стадии происходит взаимное припекание частиц, сопровождающееся увеличением площади контактной поверхности и в ряде случаев сближением их центров. На данной стадии процесса частицы сохраняют свою индивидуальность; сохраняется и понятие “контакт”.

На второй стадии спекания пористое тело может быть представлено в виде совокупности двух непрерывных фаз: фазы вещества и фазы пустоты. При этом индивидуальные поры еще не сформировались, но контакты между частицами уже исчезли и границы между элементами структуры расположены произвольно, безотносительно к их расположению между исходными частицами.

На заключительной стадии в спекающемся теле наблюдаются лишь внутрикристаллические и межкристаллические поры.

Следует учитывать, что кинетика уплотнения на всех этапах спекания определяется также и залечиванием искажений кристаллической решетки порошков.

Последовательное строгое математическое описание всех физико-химических процессов на различных стадиях спекания связано со значительными трудностями, в частности, из-за отсутствия температурных зависимостей ряда физико-химических величин и сложной геометрии пористой заготовки, особенно на втором (промежуточном) этапе спекания. Поэтому в подавляющем большинстве случаев процессы спекания описываются математическими моделями, а отдельными явлениями, усложняющими процесс, пренебрегается. Также необходимо отметить, что подробное математическое описание приводится для начальных и заключительных стадий спекания. Также, для упрощения описания, в большинстве случаев в качестве исходной системы принимается модель, предполагающая контакт двух сферических частиц в точке. Иные случаи контакта твердых частиц неправильной формы оговорены особо.

В представленном читателю учебном пособии уделено внимание и формально-кинетическому описанию процесса спекания, а также приведены результаты экспериментальных работ авторов в области исследования спекания тугоплавких неметаллических материалов, главным образом кислородсодержащих.

Механизм вязкого течения

Конкретный механизм переноса массы вследствие течения существенно зависит от структуры вещества частиц. В случае аморфного вещества вязкое течение осуществляется путем кооперативного перемещения атомов или ионов, и коэффициент вязкости η является константой вещества, определяющей скорость течения. Для кристаллических тел вязкое течение вещества может осуществляться вследствие диффузионно-вязкого преобразования формы или вследствие диффузионного восхождения дислокаций. Как и в случае аморфных тел, этот процесс непороговый (предел текучести равен нулю), однако перемещение атомов (ионов) не является процессом кооперативным, а есть следствие независимых элементарных актов диффузионного перемещения под влиянием давления, приложенного извне, которое при «свободном» спекании обусловлено кривизной поверхности приконтактного перешейка.

Вне зависимости от конкретного механизма, вязкое течение вещества в область приконтактного перешейка сопровождается и увеличением площади контакта, и сближением центров контактирующих сфер (см. соотношение 1.4).

Задачу о кинетике припекания сферических крупинок вследствие вязкого течения вещества изложим, следуя следующей логике. Будем предполагать, что на протяжении всего процесса течения вещества в область приконтактного перешейка частицы сохраняют форму сферы R(t). При углах φ ≤ 1 (рис. 1.3) можно считать, что

R(t) ≈ R₀, x(t) ≈ R₀φ (1.6)

Свободная поверхность спекающихся сфер с изменением угла φ
изменяется по закону

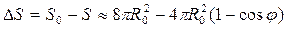(1.7)

С точностью до величин порядка φ² можно записать:

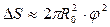, (1.8)

и соответственно работа сил поверхностного натяжения

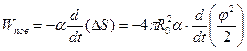. (1.9)

Для нахождения закона изменения угла φ со временем (или, что то же,
х = х(t)) работу сил поверхностного натяжения следует приравнять работе сил внутреннего трения, связанной с рассматриваемой деформацией:

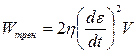, (1.10)

где – общий объем деформирующегося тела,

ε – относительная деформация тела (совокупности двух шаров).

Задача о течении вещества в область приконтактного перешейка между двумя сферическими крупинками деформация может быть охарактеризована уменьшением расстояния между центром одной из крупинок и поверхностью ее контакта с другой, так что

(1.11)

Путем математических преобразований установлено, что:

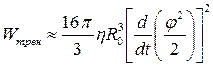(1.12)

Приравнивая (1.9) и (1.12), получим:

(1.13)

Согласно (1.6) φ ≈ x(t)/R₀, поэтому

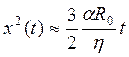(1.14)

С ростом площади контакта происходит сближение центров контактирующих сфер, расстояние между которыми l = 2(R₀ – h) определяется соотношением

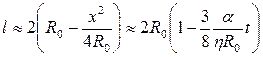(1.15)

и соответственно скорость сближения центров

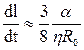. (1.16)

Характерное время t полного слияния частиц, исходный радиус которых R₀, определится соотношением *)

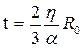, (1.17)

следующим из (1.14) в предположении x ≈ R₀.

Соотношение (1.14) экспериментально подтверждено припеканием сферических частиц стекла как к плоской стеклянной пластинке, так и между собой. Исследовано взаимное припекание сфер стекла, имевших исходный радиус 4,9∙10^{-4 см. Результаты, полученные в опытах при} T = 750 °С и 725 °С, в координатах ln (x/R₀), ln t описываются прямыми, тангенс угла наклона которых в соответствии с соотношением (1.14) равен 2.

Припекание стеклянных сфер проводили в широком интервале температур. По данным о температурной зависимости вязкости найдена энергия активации вязкого течения изучаемого сорта стекла, которая практически совпала со значением, найденным в прямых опытах.

Закон «размеров»

При обсуждении взаимосвязи между размером частиц и кинетикой процесса припекания наибольший интерес представляют два аспекта:

1. Зависимость времени, необходимого для достижения заданной степени припекания, от линейного размера частиц при данном механизме переноса вещества в область контактного перешейка;

2. Изменение относительной роли различных механизмов с изменением линейного размера частиц.

Из общих соображений следует, что время, необходимое для осуществления заданной степени припекания, должно увеличиваться с ростом линейных размеров частицы. В случае, например, сферических частиц, степень припекания количественно принято характеризовать величиной .

При условии, что исходные частицы отличаются по размеру в k раз, т.е. R₀₂ = kR₀₁, и, соответственно, x₂ = kx₁, известен закон «размеров»:

(1.52)

Величина g имеет значения, зависящие от механизма переноса массы: вязкое течение g = 1, перенос вещества через газовую фазу g = 2, объемная диффузия g = 3, поверхностная диффузия g = 4. Закон «размеров» согласуется с ранее найденными зависимостями x = f(t), и, следовательно, с экспериментальными данными.

Действительно, в случае всех рассмотренных ранее механизмов зависимость
x = f(t) может быть представлена в виде:

, (1.53)

и, таким образом,

(1.54)

Так как имеются геометрически подобные изменения формы в процессе припекания, это означает, что:

, (1.55)

(1.56)

Непосредственно закон «размеров» экспериментально изучен при взаимном припекании никелевых проволок диаметрами 1,54×10^{-4 м, 2,20}×10^{-4 м и 3,1}×10^{-4 м. Припекание исследовали при температурах 1320, 1400 и 1425} °С. Опытами, проведенными в условиях, в которых определяющим является механизм объемной диффузии, показано, что закон x⁵ ~ t выполняется в исследованном интервале температур и диаметров проволок.

Предсказанное в соответствии с законом “размеров” значение g = 3 подтверждено экспериментально (табл. 1.2).

Таблица 1.2

Параметр g в законе «размеров»

Rx/Ry	Значения g при температурах, °С:
R2/R1	3,12	2,90	3,08
R3/R1	3,08	2,92	3,18
R3/R2	3,10	2,94	3,15

Закон «размеров» может быть использован при решении вопроса о том, какой из механизмов определяет кинетику спекания в тех случаях, когда опыт проводится с прессовками, содержащими большое количество частиц. При этом важно помнить, что он получен для изотропных кристаллических тел и в реальных условиях может быть искажен зависимостью испаряемости, степени загрязненности поверхности и коэффициента поверхностной диффузии от кристаллографической ориентации различных плоскостей. Он может также нарушаться в случае, если сравниваемые частицы будут отличаться настолько существенно, что механизмы определяющие кинетику припекания, будут различными.

Относительная роль механизмов, в основном определяющих перенос массы в область контактного перешейка зависит от линейного размера частиц и при неизменном размере частицы изменяется со временем и с температурой.

Эти закономерности удобно проследить, сравнивая механизмы поверхностной и объемной диффузии, которые в наибольшей степени

вероятны при припекании частиц тугоплавких материалов.

Соотношение механизмов переноса вещества характеризуется безразмерным критерием, называемым c – фактор:

. (1.57)

В условиях изотермического опыта для достижения заданной степени припекания с, равной x/R₀, роль поверхностной диффузии будет тем большей, чем меньше линейный размер частиц, поскольку .

Роль поверхностной диффузии будет определяющей на начальной стадии процесса для частиц любого размера и сохранится до значений

(1.58)

Из (1.58) следует, что при механизм поверхностной диффузии будет определяющим до практически полного слияния частиц.

Из (1.58) также следует, что при прочих равных условиях, с ростом температуры, вследствие того, что энергия активации объемной диффузии E_v выше, нежели энергия активации диффузии поверхностной E_s, величина c будет убывать по закону и роль объемной диффузии будет возрастать. Аналогичным образом может быть проведено и сравнение других механизмов, относительная роль которых будет зависеть как от размера частиц, так и от температурной функции констант вещества.

В табл. 1.3 воедино сведены формулы, описывающие кинетику припекания при всех рассмотренных механизмах переноса вещества.

Возвращаясь к закону «размеров», следует отметить, что со значительным увеличением размера частиц наблюдается нарушение этого закона. Так, при припекании проволок, имеющих радиус от 3,8×10^{-5 м до 8,5}×10^{-4 м, показатель} n возрастает от 5 до 60. Причина указанного – в различной «активности» указанных материалов к спеканию, о чем пойдет речь в дальнейшем.

Частиц неправильной формы

Тип контакта	b	A
«Игла – игла»
«Игла – плоскость»
«Нож – нож»
«Нож – плоскость»

Третьим следствием является то, что при припекании двух игл либо иглы и плоскости имеются углы j = j*, при которых скорость роста контактного перешейка обращается в ноль. Это означает, что при j < j* энергетически целесообразным является разрыв контакта и требующееся уменьшение свободной поверхности будет происходить за счет притупления конических концов игл.

Расчеты, аналогичные приведенным, могут быть выполнены и для других механизмов переноса массы; получающиеся при этом зависимости скорости роста контактного перешейка обнаруживают закономерности, аналогичные обсужденным.

ПРИПЕКАНИЕ РАЗНОРОДНЫХ ТЕЛ

Коалесценция пор в ансамбле

В данном разделе обсуждается коалесценция ансамбля пор, удаленных от внешних и внутренних источников и стоков вакансий, т.е. процесс, который назван «внутренним спеканием».

Последовательное теоретическое описание поведения пористого тела при высокой температуре задается диффузионной теорией коалесценции дисперсных выделений новой фазы из пересыщенного раствора. Общее рассмотрение процесса диффузионной коалесценции в равной мере применимо и к случаю коалесценции выделений в двухкомпонентных твердых растворах, и к случаю, когда растворенной фазой являются вакансии. В последнем случае рассмотрение несколько упрощается, так как практически отпадает необходимость в учете влияния упругих напряжении, возникающих при росте частиц пересыщающего компонента. Обратимся к рассмотрению этой теории, имея в виду кристаллическую решетку, в которой есть избыточные вакансии и макроскопические поры. В дальнейшем будем рассматривать собственно процесс коалесценции, когда избыточные вакансии в основном выпали из раствора и пересыщение решетки вакансиями мало:

. (4.12)

Предполагая, что расстояние между порами велико по сравнению с линейным размером пор (случай «невзаимодействующих» пор), изменение радиуса поры со временем можно записать в виде

, (4.13)

где Δ = ξ – ξ₀, .

Записанное выражение справедливо в случае стационарного значения градиента dξ/dr на границе поры, что практически имеет место при условно малости начального пересыщения Δ₀. В (4.13) учтено, что концентрация вакансий у поверхности поры (ξ_R) и радиус кривизны связаны соотношением:

(4.14)

Из (4.13) следует, что при каждом пересыщении Δ есть поры, которые находятся в равновесия с раствором вакансий в решетке и имеют критический размер

. (4.15)

При R > R_k пора растет, а при R <R_k растворяется или, что то же, «поедается» более крупными. Величина пересыщения Δ, а, следовательно, и R_k ~ 1/Δ, со временем монотонно изменяется вследствие приближения системы к равновесию, когда Δ = 0 и R_k = ∞.

Первая стадия процесса, когда пересыщение еще велико ( ), заключается в выпадении вакансий из раствора. На этой стадии рост пор происходит в основном за счет коагуляции вакансий, выпадающих из раствора. Характерное время этой стадии может быть оценено следующим образом. Пусть n₀ – число растущих пор (зарождение новых пор исключается), – средний размер, до которого будут расти поры за счет вакансий «из раствора».

Тогда

, (4.16)

где Δ₀ – исходное пересыщение.

Кинетика роста пор описывается соотношением

, (4.17)

и, таким образом, продолжительность первой стадии

. (4.18)

Численная оценка t₁, при значениях величин м,
D_B = 10^-8 – 10^-9 м²/с, Δ = 10^-4 приводит к величине t₁ = 1 – 10 с.

Вторая стадия начинается тогда, когда средние размеры пор станут порядка критических ( ),что произойдет вследствие уменьшения пересыщения решетки вакансиями на первой стадии процесса. Рост пор на этой стадии будет происходить вследствие коалесценции, однако асимптотическое распределение пор по размерам еще не успеет установиться. Характерное время этой стадии оценивается соотношением

. (4.19)

При , D_B = 10^-8 м²/с, φ = 10^-12 – 10^{-13 м получаем}
t₂ = 10³ – 10⁴ с.

На заключительной стадии происходит коалесценция пор; при этом их распределение по размерам является асимптотическим и устойчивым во времени. Описанные асимптотические решения справедливы на этой стадии, т.е. когда t>>t₂.

При построении изложенной теории диффузионной коалесценции пор предполагалось, что поры имеют сферическую форму и что расстояние между ними велико по сравнению с линейными размерами, т.е. рассматривалась совокупность сферических пор, не «сталкивающихся» в том смысле, что не учитывалось возможное диффузионное взаимодействие между отдельными порами. Известно, что в связи с анизотропиейпоры будут не сферическими, а огранены плоскостями с минимальными индексами. В связи с этим величине R следует придать смысл некоторого эффективного радиуса R = (3V/4π)^1/3, где V – объем поры. Величина φ также отличается постоянным множителем, учитывающим форму пор, что принципиально не изменяет конечные формулы.

Изложенная теория коалесценции построена в предположении, что поры являются невзаимодействующими, т.е. поле напряжений и распределение концентрации вокруг каждой из пор не искажаются соответствующими полями окружающих пор. Учет возможного взаимодействия пор приводит лишь к незначительному изменению асимптотической функции распределения.

Некоторый вклад в процесс коалесценции может внести прямое столкновение пор, которые взаимно сближаются. Этот механизм может быть заметным на том этапе процесса, когда залечивание пор остановлено находящимся в них газом и образовавшиеся при этом газовые включения достаточно малы для того, чтобы их перемещение в основном определялось механизмом поверхностной диффузии.

Процессу коалесценции вследствие столкновения газовых включений способствует поле неоднородных напряжений в прессовке, под влиянием которых газозаполненные поры могут двигаться по закону ν ~ D_s/R, когда малые включения, двигаясь быстрее, настигают более крупные и сливаются с ними. Такое слияние включений выгодно, так как оно сопровождается уменьшением поверхностной энергии.

В предположении, что коалесценция осуществляется только вследствие процесса столкновений включений и что ширина δR начального распределения пор по радиусам вокруг наиболее вероятного значения R_a велика (δR ~ R_a), выполнена оценка характерного времени, в течение которого средний размер включения увеличится вдвое:

. (4.20)

При R = 10^-6 – 10^{-7 м, θ ≈ 0,1, ν = 1 – 10 Å/с величина τ} имеет порядок нескольких часов.

Описанный механизм коалесценции может оказаться существенным вблизи скопления дислокаций и при спекании в условиях, когда в прессовке поддерживаются неоднородные напряжения («гравитационные напряжения», одноосное давление и др.).

На начальной стадии процесса спекания, когда активно происходит собирательная рекристаллизация, может происходить слияние нор, которые движутся вслед за перемещающимися границами. Схематически этот тип коалесценции изображен на рис. 4.2.

Рис. 4.2. Схема слияния пор, движущихся с границами в процессе рекристаллизации

Изучена временная зависимость среднего размера пор в условиях, близких к теоретическим. В качестве объекта исследования избраны кристаллы каменной соли. В исходном состоянии эти кристаллы содержали мелкие поры ~ 10^{-7 м}. На далеких стадиях высокотемпературного отжига в кристалле вследствие процесса коалесценции формировались оптически видимые поры. Найденная в этих экспериментах зависимость изображена на рис. 4.3 и свидетельствует о выполнимости закона .

Рис. 4.3. Временная зависимость среднего размера пор по данным опытов с дефектными кристаллами NaCl

Изучена коалесценция пор для корундовых прессовок в широком диапазоне температур и времен отжига. Результаты опытов свидетельствуют о том, что идущее со временем уменьшение числа и объема пор сопровождается ростом их среднего размера. На далеких стадиях процесса спекания появляются поры, размер которых превосходит размер наибольших пор, имевшихся в прессовке до спекания.

Опытами по коалесценции пор в меди гальванического происхождения показано, что имеет место предсказываемая теорией зависимость

(4.21)

Экспериментально отчетливо отделить диффузионную коалесценцию от коалесценции, происходящей вследствие прямого столкновения пор, на ранней стадии процесса спекания прессовок из дисперсных порошков не представляется возможным: оба эти процесса происходят одновременно и во взаимосвязи.

Извне приложенное давление всестороннего сжатия может оказать существенное влияние на процесс коалесценции, так как под давлением изменяется критический радиус поры (R_P^*,[см. формулу (3.15)]. При этом некоторые поры, которые в отсутствие давления относились к категории «надкритических» (R > R_Р^*),под влиянием давления перейдут в разряд «подкритических» (R < R_Р^*), т.е. залечивающихся. Так как при величина R_P^* обращается в бесконечность, то сравнительно небольшое давление Р = 10 – 10² атм. может существенно повлиять на залечивание пор в кристалле.

Стадии процесса усадки

Впрактике порошковой металлургии и технике получения тугоплавких неметаллических материалов явление спекания используется в системах, характеризующихся наличием весьма значительных искажений кристаллической решетки. Дисперсные порошки, предназначенные для изготовления изделий, как правило, получают в условиях, при которых в их кристаллической решетке образуются искажения различных типов. Степень дефектности кристаллической решетки порошков частично возрастает также при их прессовании. Таким образом, порошковая прессовка удалена от состояния термодинамического равновесия не только в связи с развитостью свободной поверхности, но одновременно и по многим иным параметрам: вследствие наличия избыточных вакансий, дефектов упаковки, дислокации, микроскопических пор внутри частиц и др. В процессе высокотемпературного обжига пористой порошковой прессовки одновременно с собственно спеканием, когда уплотнение сопровождается уменьшением свободной поверхности, происходит и залечивание дефектов кристаллической решетки порошков.

Из общих соображений следует, что кинетика собственно спекания и кинетика процессов залечивания дефектов решетки должны быть тесно взаимосвязаны.

Об определяющем влиянии процесса залечивания искажений на кинетику усадки свидетельствует то, что со временем изотермического отжига пористость убывает медленнее, чем скорость усадки.

Известно, что эффективная диффузионная подвижность атомов (ионов) в дефектных структурах повышена, и можно было бы предполагать, что дефектность кристаллической решетки порошков в прессовке себя проявит лишь количественно, обусловив ускорение процесса спекания в меру увеличенной (по сравнению с «равновесной») диффузионной подвижности атомов (ионов). В действительности, однако, наличие дефектов кристаллической решетки приводит к появлению некоторых особенностей и механизме уплотнения, несвойственных пористым структурам, где наличие пор – единственный признак неравновесности.

В производственной и лабораторной практике широко известны приемы так называемого «активированного» спекания, заключающиеся в искусственном увеличении степени дефектности порошков. Скорость уплотнения прессовок из таких порошков существенно возрастает. Так, например, прессовки из порошков, синтезированных электролитически при большой плотности тока, при прочих равных условиях уплотняются с существенно большей скоростью, чем из порошков, полученных механическим измельчением.

Предыдущий анализ кинетики свидетельствует о том, что свободное спекание в отсутствие жидкой фазы является ползучестью под влиянием сил поверхностного натяжения. Это утверждение, ранее обсуждавшееся применительно к «бездефектным» пористым структурам, остается справедливым применительно к пористым структурам с дефектной кристаллической решеткой. Кривые, описывающие кинетику удлинения реального кристаллического тела в процессе ползучести и усадку пористой порошковой прессовки при спекании на ранней стадии процесса, весьма подобны. Главная особенность процессов, описываемых этими кривыми, заключается в том, что в изотермических условиях со временемих скорость убывает. Эта особенность кинетики качественно объясняется тем, что одновременно с ползучестью и усадкой происходит залечивание дефектов решетки. Вследствие залечивания дефектов перемещение вещества (безотносительно к конкретному механизму процесса) становится более затрудненным.

Конкретный тип дефектов, оказывающих преобладающее влияние на кинетику усадки, и механизм этого влияния оказываются различными в различных температурных областях и изменяются со временем изотермического отжига. Изменяется также геометрия двухфазной смеси «вещество – пустота». В связи с этим единое последовательное описание кинетической кривой усадки, которое основано на конкретной модели дефекта, определяющего «активность» порошков, и модели геометрии смеси «вещество – пустота», пригодное в широком диапазоне температур и времен, не может быть выполнено. Можно, однако, кривую усадки разделить на участки, каждый из которых описывает кинетику спекания в условиях, когда могут быть указаны и тип дефекта, и признаки геометрии фазы пустоты, которые определяют механизм усадки.

Условно процесс усадки (уплотнения) удобно представить в виде последовательности трех стадий.

Ранняя стадия. На этой стадии, когда плотность прессовки еще мала (в предельном случае – совокупность свободно насыпанных порошков), понятие «пора» лишено содержания и кинетика уплотнения в основном определяется процессами, происходящими в месте контакта порошинок. В этом случае существенную роль играет не только структурное состояние, но и геометрия порошинок. Для этой стадии характерна весьма высокая скорость деформирования частиц, приводящего к усадке прессовки.

Промежуточная стадия. На этой стадии «фаза пустоты» может быть представлена как совокупность неизомерных пор с некоторым средним характерным размером R. Искажения кристаллической решетки велики и среднее расстояние между возможными источниками и стоками вакансий l << R, т.е. рассматривавшийся ранее безразмерный параметр 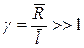. На этой стадии уменьшение объема каждой из пор может происходить практически независимо и пористая матрица в процессе спекании ведет себя как вязкая среда с коэффициентом вязкости 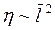. Уплотнение пористого тела при этом равномерно во всем его объеме (при условии равномерного распределения пор). Подобно тому, как это имеет место в аморфных телах, коалесценция пор может происходить лишь в случае их слияния.

Поздняя стадия. Вследствие залечивания искажений и процесса рекристаллизации безразмерный параметр может измениться, достигнув значении γ<<1. В этом случае залечивание отдельной поры будет происходить вследствие ее диффузионного растворения в матрице. Важная особенность этой стадии процесса заключается в диффузионном взаимодействии между порами, делающем возможным процесс коалесценции, когда уменьшение поверхности пор происходит при их неизменном суммарном объеме (внутреннее спекание).

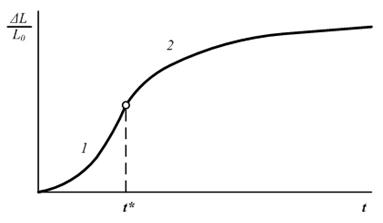
Рис. 5.1. Кинетическая кривая усадки (схема)

Отчетливой границы между этими тремя стадиями, разумеется, нет. На промежуточной стадии уплотнение реальной заготовки в ее различных микрообъемах может определяться процессами, характерными для ранней и поздней стадий.

Имея в виду, что заметная усадка происходит за время нагревания заготовки до температуры и