Способ вращения вокруг проецирующей прямой
Общие сведения о способе вращения вокруг проецирующей прямой. Способ вращения вокруг проецирующей прямой относится к способам преобразования эпюра, когда объект в пространстве меняет своего положения, а положение проецирующего аппарата не изменяется.
Рассмотрим суть данного способа.
Дана ось i, перпендикулярная к плоскости проекций π1, и точка А, вращающаяся вокруг нее в плоскости β, параллельной плоскости π1 и одновременно перпендикулярной к оси вращения i. (рис. 67)
При вращении точка А перемещается по окружности в плоскости вращения β. Центр окружности является точкой пересечения оси вращения с плоскостью вращения и называется центром 0 вращения, а расстояние от точки А до центра вращения - радиусом вращения. Траектория точки А на плоскость π1 проектируется окружностью, а на плоскость π2 - отрезком прямой, параллельным оси 0Х (рис. 68).
Следует отметить, если ось вращения будет перпендикулярна плоскости проекций π2, тогда траектория точки на плоскость π2 будет проектироваться окружностью, а на плоскость π1 - отрезком прямой, параллельным оси 0Х.
Отсюда общее правило, если точка вращается вокруг оси, перпендикулярной к плоскости проекций, то проекция точки на этой плоскости перемещается по окружности, а другая проекция - по прямой, перпендикулярной к проекции оси вращения (или параллельно оси проекций).
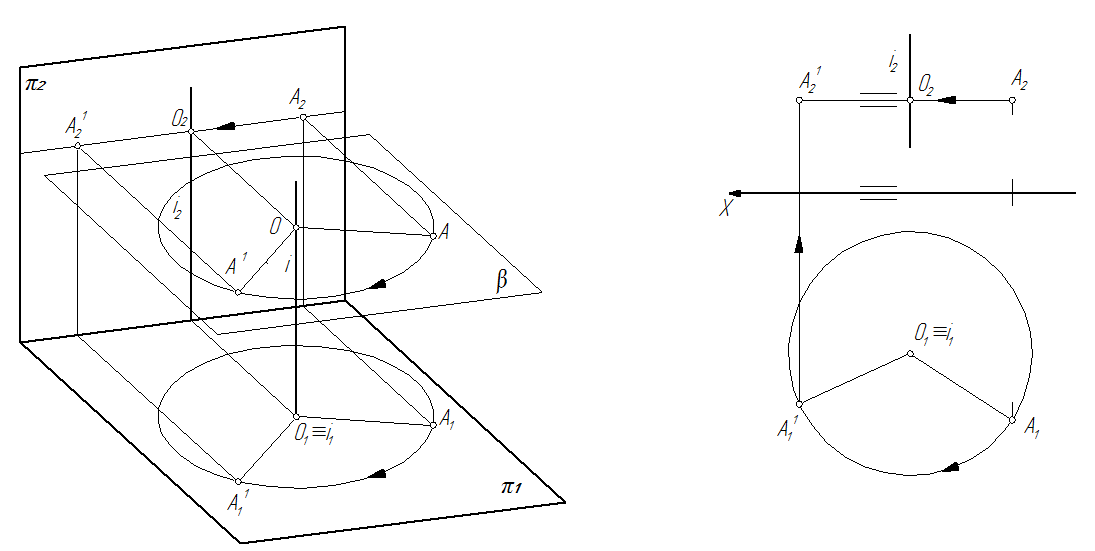
Рис. 67 Рис. 68
3адача 1. Определить натуральную величину двугранного угла.
Для решения задачи необходимо линию пересечения плоскостей (граней) преобразовать в проецирующие положение. Тогда заданные плоскости преобразуются в проецирующие плоскости и угол между вырожденными в прямые проекциями плоскостей и есть искомая величина.
Рассмотрим решение задачи на примере двугранного угла, образованного треугольниками ∆AВD и ∆BCD. Исходные данные:A(25; 45; 40), B(50; 10; 20), C(20; 15; 10) и D(10; 25; 35).
Решение (рис. 69). В общем случае задача решается двумя вращениями.
При первом вращении отрезок [BD] преобразуется в отрезок уровня (горизонталь). Для этого ось вращения i выбирается в виде фронтально-проецирующей прямой, проходящей через точку В. Далее проекцию отрезка [B2D2] поворачивают до положения параллельного оси 0Х (характерный признак горизонтали): [B12 D12] ∥ 0Х. При этом повороте горизонтальная проекция отрезка [B11 D11] становится натуральной величиной.
При втором вращении отрезок уровня преобразуется в проецирующий (фронтально-проецирующий) отрезок. Для этого ось вращения j выбирается в виде горизонтально-проецирующей прямой, проходящей через точку D1. Далее проекцию отрезка [B11 D11] поворачивают до перпендикулярного положения относительно оси 0Х (характерный признак фронтально-проецирующей прямой): [B21 D21] ⊥ 0Х. При этом плоскости треугольников ∆AВD и ∆BCD преобразуются в проецирующие (фронтально-проецирующие) плоскости. Угол между проекциями треугольников ∆A22B22D22 и ∆B22C22D22 является искомой величиной.
Варианты заданий приведены в табл. 11.
3адача 2. Определить натуральную величину треугольника.
Рассмотрим решение задачи на примере определения натуральной величины треугольника ∆АВС. Исходные данные: A(25; 45; 40), B(50; 10; 20) и C(20; 15; 10).
Решение. Задача решается двумя вращениями (рис. 70).
При первом вращении плоскость треугольника преобразуется в проецирующее положение. Для этого горизонталь h плоскости ∆АВС преобразуют во фронтально-проецирующею прямую вращением ее вокруг оси i, проходящей через точку В.
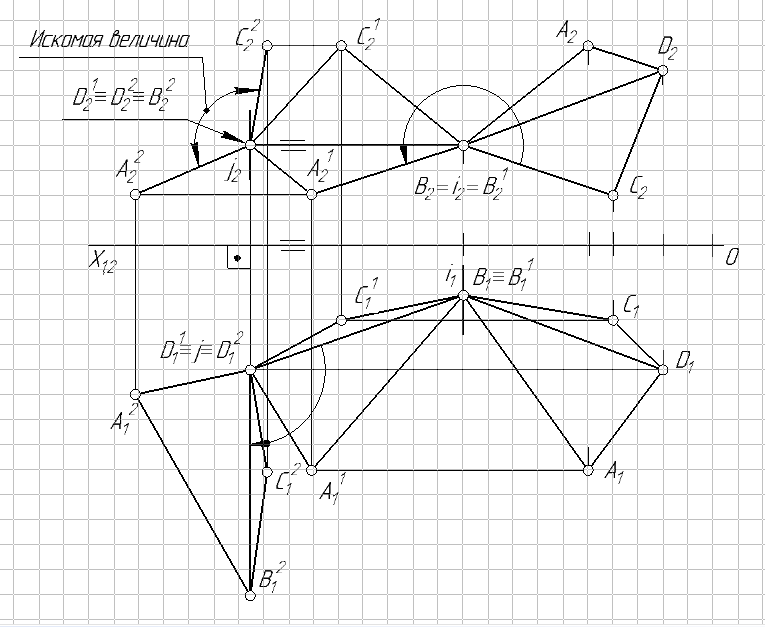
Рис. 69
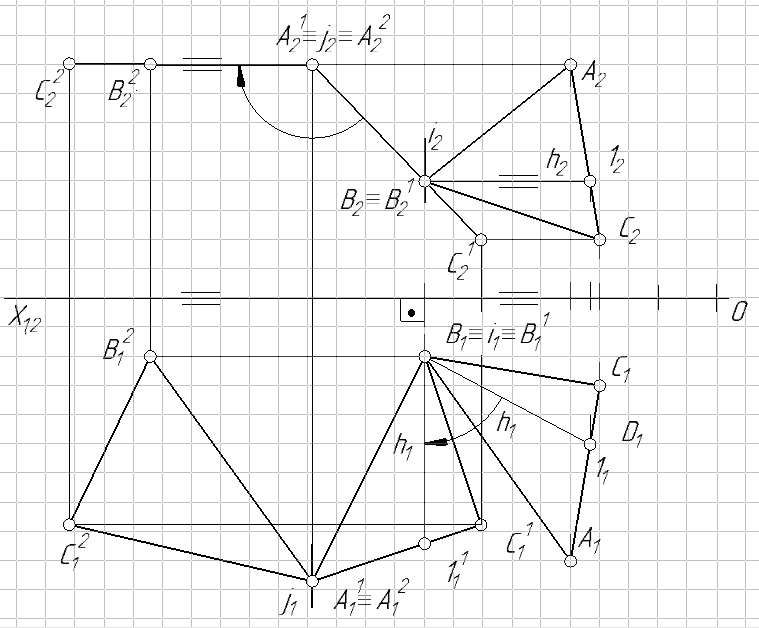
Рис. 70
При втором преобразовании вырожденную проекцию плоскости ∆А12В12С12 вращением вокруг оси j, проходящей через точку А1 до параллельности ее оси 0Х (характерный признак горизонтальной плоскости уровня): ∆А12В12С12 → ∆А22В22С22 ∥ 0Х. Следовательно горизонтальная проекция треугольника ∆А21В21С21 будет является натуральной величиной треугольника ∆АВС: ∆А21В21С21 =∆АВС.
Варианты заданий приведены в табл. 11.
Таблица 11
Исходные данные по теме «Метрические задачи»
| Вариант | Численные значения координат точек | |||||||||||
| А | В | С | D | |||||||||
| x | y | z | x | y | z | x | y | z | x | y | z | |
ПОВЕРХНОСТИ
