Минимаксные (игровые) задачи синтеза. достаточные условия оптимальности

В предыдущих разделах были рассмотрены методы ре­шения задач синтеза при предположении, что о действующих воз­мущениях известны все статистические характеристики. Однако во многих случаях информация, которой мы располагаем, является неполной и в статистическом смысле. В одних случаях статистиче­ские характеристики возмущений известны лишь с точностью до некоторых параметров. Например известно, что возмущение явля­ется гауссовским, но величины математического ожидания и дис­персия точно не известны, известны только пределы их изменений. В других случаях статистические характеристики вообще неизвестны, известно лишь, что возмущения относятся к некоторому классу, например значения возмущений по абсолютным величинам не мо­гут превосходить некоторых значений. В обоих случаях имеет мес­то неопределенность. Для принятия решения о выборе структуры управления в условиях неопределенности обратимся к минимакс­ному подходу — будем считать оптимальным управление, которое обращает в минимум наибольшее (по возмущениям) значение кри­терия. Значение критерия, соответствующее этому управлению, будем называть гарантированным, а саму стратегию управления — гарантирующей.

К минимаксным задачам приходим и в случаях игровых ситуа­ций, когда в процессе управления действуют две стороны, стремя­щиеся к противоположным целям. При этом стратегия одной из сторон может быть условно отнесена к возмущению с неопределен­ностью. Справедлива и обратная трактовка: любая минимаксная задача, в том числе и задача синтеза оптимального управления с неопределенностью по возмущению, может рассматриваться как игровая задача. В качестве второго «игрока», стремящегося проти­водействовать выбору оптимального управления, выступает в дан­ном случае сама природа.

Рассмотрим задачу управления следующей дискретной сис­темой:

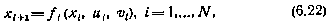
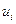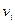где — вектор состояния системы в i-й момент времени; , — векторы управления; 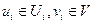. Пусть критерием качества является функция конечного состояния

Полагаем, что управление 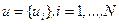, стремится обратить критерий (6.23) в минимум, в то время как управление 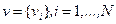, стремится его максимизировать. При этом считаем, что выбор управления любой стороной производится на каждом шаге управления, причем в распоряжении каждой стороны имеется пол­ная информация как о состоянии системы, так и о стратегии проти­воположной стороны, предшествующей выбору текущего управ­ления.

Рассмотрим задачу определения гарантирующей стратегии управления 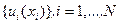, т.е. задачу отыскания величины

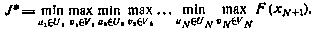
Введем в рассмотрение функцию будущих потерь

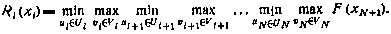
Как и прежде, функция 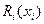определяет наилучшее значение критерия (6.23), которое может быть достигнуто при движении системы (6.22) из состояния в момент i.

Очевидно, функция 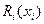удовлетворяет следующему рекур­рентному соотношению:

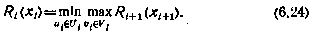
Из определения функции 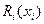формально получаем следую­щее граничное условие:

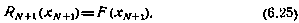
Так как последовательность управлений 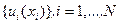, най­денная с помощью соотношений (6.24), обеспечивает наилучшее значение критерия (6.23), то совокупность соотношений (6.24) при 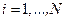с учетом (6.25) может рассматриваться как достаточные условия оптимальности при определении гарантирующей стратегии управления 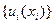системой (6.22) с критерием (6.23).

Как и прежде, можно показать, что в задаче определения га­рантирующей стратегии управления системой (6.22) с критерием более общего вида

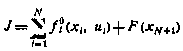
достаточные условия оптимальности принимают вид рекуррентного соотношения

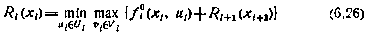
с прежним граничным условием