Оптимальное управление конечным состоянием спускаемого аппарата
Рассмотрим задачу синтеза оптимального управления одномерным конечным состоянием спускаемого летательного аппарата. В качестве управляющей силы считаем аэродинамическую силу, создаваемую за счет изменения угла крена аппарата. Цель управления состоит в обеспечении минимального рассеивания точек приземления аппарата, возникающего как за счет начальных ошибок, так и за счет действия атмосферных случайных возмущений (порывы ветра, вариации плотности воздуха).
Для простоты ограничимся случаем движения в вертикальной; плоскости. В качестве независимой переменной примем высоту полета. Тогда уравнения движения аппарата могут быть представлены в виде
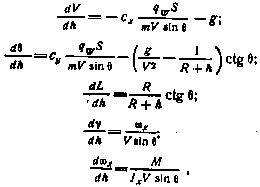
где V — скорость ЛА;  — угол наклона траектории; L— продольная дальность; h — высота полета;
— угол наклона траектории; L— продольная дальность; h — высота полета; 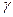 - угол крена;
- угол крена;  — угловая скорость ЛА; сх, су — коэффициенты лобового сопротивления и подъемной силы соответственно;
— угловая скорость ЛА; сх, су — коэффициенты лобового сопротивления и подъемной силы соответственно; 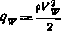 - воздушный скоростной напор; Vw — воздушная скорость ЛА; S—площадь миделя; m — масса аппарата; g — ускорение силы тяжести; R — радиус Земли; М — управляющий момент по крену
- воздушный скоростной напор; Vw — воздушная скорость ЛА; S—площадь миделя; m — масса аппарата; g — ускорение силы тяжести; R — радиус Земли; М — управляющий момент по крену 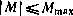 , Jx — момент инерции относительно оси симметрии;
, Jx — момент инерции относительно оси симметрии; 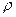 — плотность атмосферы.
— плотность атмосферы.
Уравнения движения получены в предположении, что влияние порывов ветра на движение ЛА сводится лишь к изменению аэродинамических сил за счет изменения скорости V воздушной скоростью Vw. Если через W обозначить скорость горизонтальных порывов ветра, то нетрудно установить связь Vw и V:
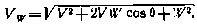
В первом приближении атмосферные возмущения могут быть представлены с помощью линейных нестационарных формирующих фильтров. При этом для ветра можно ограничиться фильтром первого порядка, а для вариации плотности 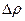 атмосферы — фильтром второго порядка:
атмосферы — фильтром второго порядка:
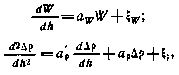
где aw, ар' ар, а также интенсивности Nw и Np белых шумов 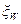 и
и 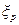 подбираются таким образом, чтобы статистические характеристики (например, корреляционные функции) возмущений как можно точнее соответствовали действительным характеристикам.
подбираются таким образом, чтобы статистические характеристики (например, корреляционные функции) возмущений как можно точнее соответствовали действительным характеристикам.
Вводя обобщенный вектор состояния
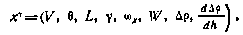
приходим к уравнению
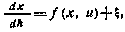
где f(x,u) —вектор-функция, элементы которой получаются из правых частей представленных выше уравнений u =М — управляющее воздействие; 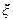 — вектор белых шумов
— вектор белых шумов 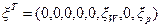 . Задача синтеза оптимального управления заключается в определении такого закона u(x,h), который обеспечивает минимум дисперсии координаты x3 = L в конечный момент времени, т. е. при u = 0. Итак, критерий оптимальности равен
. Задача синтеза оптимального управления заключается в определении такого закона u(x,h), который обеспечивает минимум дисперсии координаты x3 = L в конечный момент времени, т. е. при u = 0. Итак, критерий оптимальности равен

Предположим, что возмущенное движение ЛА с достаточной точностью описывается уравнениями в отклонениях относительно некоторой номинальной траектории спуска. Тогда, проводя линеаризацию нелинейных уравнений, получим линеаризованную модель движения
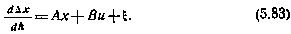
Здесь под Δх понимается вектор, равный разности между истинным вектором х и вектором, вычисленным на номинальной траектории при одинаковых h; А — матрица; В — вектор частных производных правых частей по компонентам вектора х и управлению и соответственно. Естественно, что А и В зависят от высоты полета h.
Для решения задачи обратимся к достаточным условиям оптимальности. Однако, учитывая скалярный вид критерия оптимальности (5.82), предварительно произведем следующее преобразование задачи. Введем в рассмотрение новый вектор у, связанный с вектором х соотношением

где Ф(0,h) —фундаментальная матрица системы (5.83), удовлетворяющая уравнению
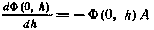
при условии Ф(0,0)=I.
Отметим, что в соответствии с определением вектора у в момент h = 0 имеет место равенство
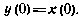
Дифференцируя (5.84) по h и принимая во внимание уравнение (5.83), получаем следующее уравнение для вектора у:
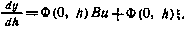
Так как критерий оптимальности (5.82) может быть представлен в виде
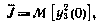
а компонента у3 не зависит от других компонент вектора у, то вместо уравнения для вектора у можно ограничиться лишь одним уравнением для компоненты у3:

где 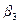 ,
, 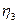 — третьи компоненты векторов Ф(0,h)В и Ф(0,h)
— третьи компоненты векторов Ф(0,h)В и Ф(0,h) 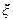 соответственно.
соответственно.
Таким образом, введение вектора у позволило рассматриваемую задачу свести к скалярной. Теперь воспользуемся уравнением Беллмана, которое в данном случае принимает вид
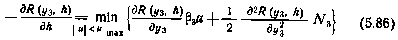
с граничным условием R(у3,0) = у32(0). Через N3 обозначена интенсивность белого шума 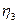 , umax=Mmax.
, umax=Mmax.
Из уравнения (5.86) получаем структуру оптимального управления
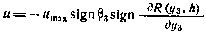
Таким образом, оптимальное управление является релейным. Из физических соображений ясно, что функция будущих потерь R(у3,h) является четной и возрастающей по 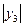 функцией. Поэтому
функцией. Поэтому
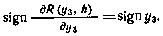
С учетом этого окончательно закон оптимального управления принимает вид
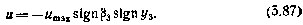
Таким образом, задача синтеза оптимального управления одномерным конечным состоянием линейной системы решена полностью. Однако провести анализ точности, т. е. решить уравнение (5.86), аналитически и здесь не удается.
