Достаточные условия оптимальности. метод динамического программирования

Рассмотрим задачу управления дискретной стохастиче­ской системой, описываемой уравнением

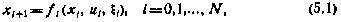
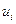где по-прежнему считается, что — n-мерный вектор состояния; — m-мерный вектор управления, принимающий значения из до­пустимого множества 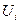; 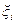- q-мерный вектор случайных возму­щений, независимых для разных моментов времени; 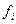— n -мерная вектор-функция. Начальное значение вектора х₀ считается задан­ным.

Критерий оптимальности также зададим в виде математического ожидания от некоторой терминальной функции

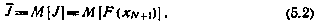
Однако в отличие от программирования управления будем счи­тать, что в процессе управления в любой текущий момент i может быть точно измерен полный вектор состояния . Ставится задача отыскания такого алгоритма (закона) управления системой (5.1), т. е. последовательности зависимостей 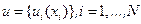, кото­рый обеспечивает перевод системы (5.1) из начального состояния х₀ в некоторое конечное состояние с минимальным значением критерия (5.2).

Покажем, что применение метода динамического программиро­вания в данной задаче обеспечивает выполнение достаточных усло­вий оптимальности. Для этого введем в рассмотрение функцию будущих потерь

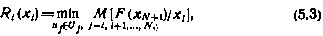
представляющую собой минимальное значение исходного критерия (5.2), которое может быть достигнуто при оптимальном управлении системой (5.1), начиная с момента времени i из состояния . Сим­вол M[.../ ] означает условное математическое ожидание.

Раскрывая в (5.3) операцию математического ожидания, исполь­зуя правило пересчета переходных плотностей вероятностей марков­ского процесса и применяя поэтапную оптимизацию, можно записать

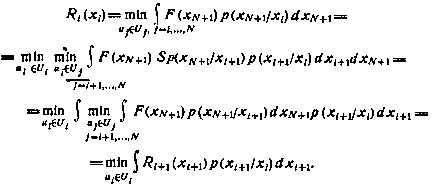
Здесь через 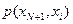обозначена переходная плотность вероятно­стей процесса (5.1) при управлении 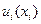, т. е. условная плотность вероятностей вектора 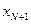при фиксированных значениях 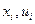. Ин­тегралы всюду следует понимать как многомерные с областями интегрирования, совпадающими с областями изменения векторов 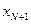, 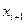соответственно.

Другими словами, функция будущих потерь 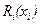, определяе­мая соответственно (5.3), удовлетворяет рекуррентному соотноше­нию

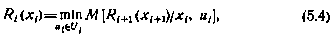
называемому также основным рекуррентным соотношением метода динамического программирования. Так как для последнего момен­та управления i = N по определению имеем

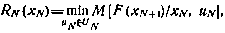
то граничное условие для рекуррентного соотношения (5.4) может быть формально записано в виде

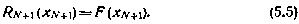
Применяя соотношение (5.4) последовательно начиная с мо­мента i = N, получаем при i — 0 величину 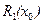, которая согласно (5.3J представляет собой минимальное значение критерия (5.2):

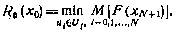
Другими словами, последовательность управляющих воздейст­вий 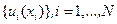, вычисленная в соответствии с рекур­рентным соотношением (5.4) с учетом граничного условия (5.5), оп­тимальна.

Таким образом, соотношения (5.4) с учетом (5.5) можно рас­сматривать как достаточные условия оптимальности в задаче син­теза оптимального управления системой (5.1) с критерием (5.2).

Нетрудно показать, что если критерий оптимальности вместо (5.2) имеет более общий вид

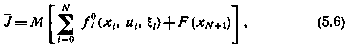
то достаточные условия оптимальности могут быть представлены в виде рекуррентного соотношения

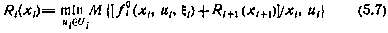
с прежним граничным условием

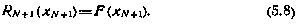
Действительно, вводя дополнительную переменную 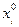, опреде­ляемую согласно уравнению

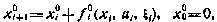
критерий (5.6) сведем к виду (5.2) по отношению к расширен­ному вектору состояния (х°, х):

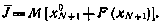
Применим формально основное рекуррентное соотношение (5.4) с учетом (5.5). Получим

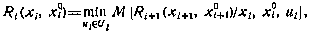
причем

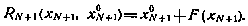
Для момента i=N функция 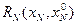может быть представлена в виде

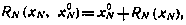
где

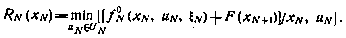
Аналогично для момента i=N—1

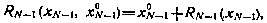
где

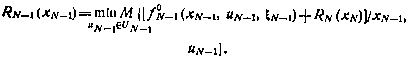
Для произвольного момента

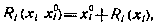
где

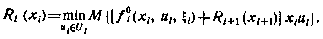
Нетрудно видеть, что компонента 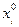не влияет на выбор опти­мального управления. Поэтому ее можно исключить из рассмотре­ния, ограничившись рекуррентным соотношением для функции

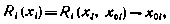
которое совпадает с соотношением (5.7).

Граничное условие для функции 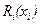по построению имеет вид (5.8).