Определение орбиты искусственного спутника Земли с использованием метода наименьших квадратов

В соответствии с классической постановкой задачи опре­деления орбиты ИСЗ с использованием метода наименьших квад­ратов определим начальные условия движения ИСЗ на момент прохождения им экваториальной плоскости Земли. Схема опреде­ления орбиты ИСЗ приведена на рис. 3.15. Пусть орбита определя­ется по измерениям даль­ности с наземных измери­тельных пунктов — НИПов, число которых варьируется, .например, от одного до трех. Тогда на каждом витке по­лета ИСЗ может быть про­ведено от одного до трех се­ансов измерений. С целью выявления особенностей про­цедуры метода наименьших квадратов (МНК) примем достаточно простые матема-

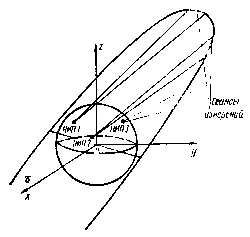
Рис. 3.15. Схема организации экс­перимента по определению орбиты ИСЗ

тические модели движения и измерений. Иначе говоря, учтем толь­ко основные факторы, определяющие сложность вычислительной процедуры,— нелинейность уравнений движения и соотношений для измерений.

Уравнения движения ИСЗ в центральном поле тяготения Зем­ли, в экваториальной системе координат, имеют вид

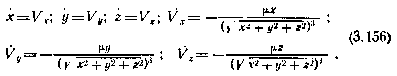
Расчетные (опорные) начальные условия для этой системы уравнений определяются расчетной орбитой выведения и точно­стью выведения ИСЗ носителем. В стохастической интерпретации применительно к байесовской постановке задачи это означает, что начальные условия для системы уравнений (3.156) представляют собой случайный вектор Х(0) с компонентами х(0) =х₀,

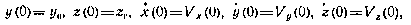
с заданным математическим ожиданием 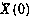и корреляционной матрицей Р_х (0).

Предположим, что наземный измерительный пункт (НИП) со­вершает плоское движение по окружности в плоскости, параллель­ной плоскости экватора, с угловой скоростью, равной угловой ско­рости Земли. В таком случае определены экваториальные коорди­наты НИП:

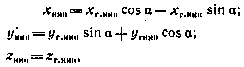
где 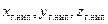— координаты НИП в гринвичской системе координат; 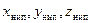— координаты НИП в абсолютной эква­ториальной системе координат;

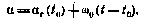
Здесь - момент, к которому «привязываются» начальные усло­вия x_о; — угловая скорость Земли; 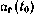—-прямое восхожде­ние гринвичского меридиана на момент ;t и — среднее солнеч­ное время. Модель измерения дальности — простейшая. Считаем, что с наземных измерительных пунктов измеряется дальность р, связанная с координатами ИСЗ и НИП соотношением

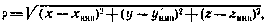
причем измерения осуществляются дискретно в моменты 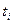и соп­ровождаются центрированными некоррелированными ошибками 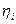со средним квадратичным отклонением 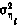, так что можно записать

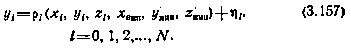
Перейдем к описанию вычислительной процедуры, реализую­щей алгоритм метода наименьших квадратов.

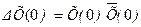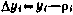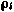Обозначим , где Х(0)—искомый «истин­ный» вектор начальных условий движения ИСЗ; где — расчетное значение дальности в момент 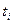соответствующее движению ИСЗ из искомых «истинных» начальных условий Х(0). Тогда, линеаризуя зависимость дальности от начальных условий в окрестности точки Х(0), можно записать

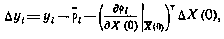
где 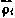— расчетное значение дальности в момент 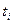,соответству­ющее движению ИСЗ из начальных условий 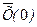. Приведенное выражение удобно переписать в виде

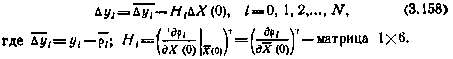
Производные 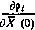называются баллистическими.

Уравнения (3.158) называются условными, если измерения име­ют различную физическую природу или не являются равноточны­ми. В последнем случае вводят так называемые веса измерений

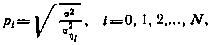
причем значение 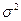— произвольное, и уравнения (3.158) принима­ют вид

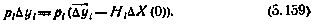
Как уже указывалось, алгоритм метода наименьших квадратов определяется из условия минимизации суммы квадратов невязок 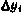, взятых в случае неравноточных измерений с весами p_i.

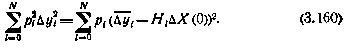
Минимизация (3.160) по 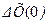приводит, как известно (см. (3.144), к следующим уравнениям относительно :

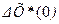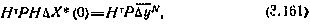
где 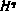—блочная матрица 6×(N+l) вида ;

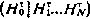Р- диагональная матрица (N+l) × (N+1) с элементами р_i²;

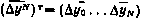- вектор (N+1)×1.

Уравнение (3.161) называют нормальным уравнением. Обозна­чим А = Н^ТРН и В = Н^ТР. Элементы a_kn матрицы А и b_k матрицы В можно записать в скалярной форме:

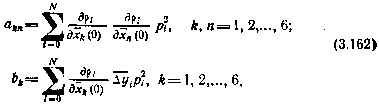
Где 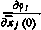частные производные от измеряемого параметра p_i по определяемым начальным условиям. Их удобно записать в форме

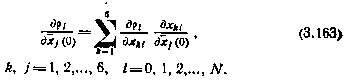
В этом выражении 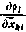- частные производные от измеряемых . параметров по компонентам вектора состояния 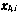, вычисленные в момент 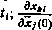- частные производные от компонент вектора состояния ИСЗ 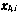по начальным условиям 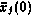, вычисленные в момент 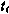. Существуют различные вычислительные алгоритмы ме­тода наименьших квадратов, отличающихся способом определения частных производных, входящих в (3.163). Используем для опреде­ления этих частных производных метод конечных разностей. Частные производные 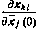определяются численным дифференцированием по следующей схеме. Задаются начальньши условиями

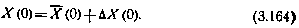
Здесь 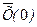—априорные расчетные (опорные) начальные условия,, используемые в качестве начального (нулевого) приближения в алгоритме наименьших квадратов. Вектор 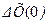при вычислении производной 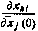формируется следующим образом: 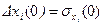, где 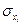— априорное среднеквадратичное отклонение компоненты вектора состояния ИСЗ, соответствующее априор­ной корреляционной матрице P_x(0). Для остальных компонент 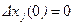; j — 2...6. При начальных условиях (3.164) численно ин­тегрируются уравнения движения ИСЗ (3.156) и рассчитываются значения 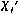вектора состояния ИСЗ на все требуемые моменты i=l, 2, ..., N. Затем принимаются начальные условия

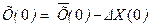
и при этих начальных условиях точно также рассчитываются зна­чения вектора состояния ИСЗ 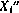, i=l, 2,..., N. Частные производ­ные 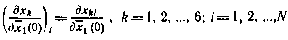определяются по формуле

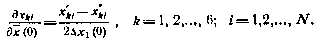
Аналогично рассчитываются частные производные компонент 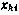текущего вектора состояния ИСЗ 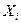по другим компонентам 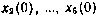вектора начальных условий Х(0). Частные произ­водные измеряемых параметров по компонентам текущего вектора состояния могут быть рассчитаны по их явным выражениям на ос­нове рассчитанных текущих значений компонент 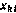вектора 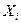. Заметим, что с целью уменьшения объема вычислений при опреде­лении производных 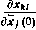можно использовать более простые выражения

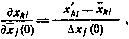
где 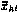— значение k-й компоненты вектора состояния момент 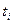при начальных условиях .

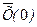С целью дальнейшего уменьшения затрат машинного времени при прогнозировании состояния ИСЗ на моменты 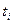(i=1, 2,..., N) можно вместо численного интегрирования уравнений (3.156) воспользоваться приближенным аналитическим методом по следую­щей схеме. Вначале осуществляется переход от вектора состояния Х(0) с компонентами 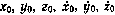в декартовых экваториаль­ных координатах к вектору элементов орбиты в следующей после­довательности. Определяются:

большая полуось орбиты

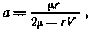
где

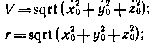
фокальный параметр

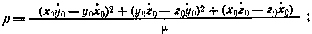
Эксцентриситет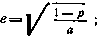

Наклонение

долгота восходящего узла

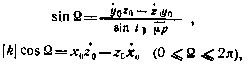
где k — произвольный множитель (это равенство определяет cos );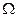

аргумент широты ИСЗ

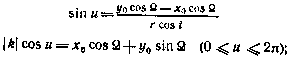
истинная аномалия

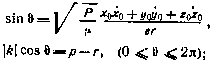
аргумент перицентра

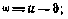
эксцентрическая аномалия

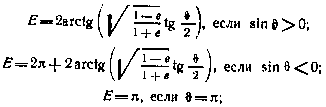
время прохождения перигея

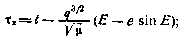
период обращения ИСЗ

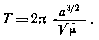
Определим эксцентрическую аномалию Е_i, соответствующую» положению ИСЗ на требуемый расчетный момент 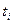из уравнения Кеплера:

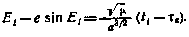
Это уравнение обычно решают методом итераций, представляя егов виде

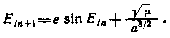
Затем определяется истинная аномалия:

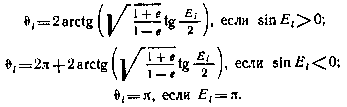
Далее определяются долгота, радиус-вектор, радиальная и трансверсальная составляющие скорости ИСЗ для расчетного мо­мента .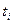

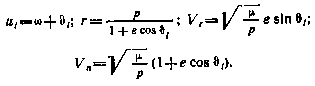
Затем определяются компоненты вектора 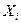в экваториальной системе координат:

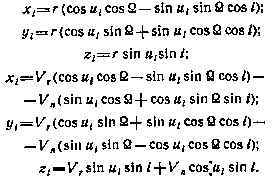
Таким образом, последовательность действий при реализации вычислительной процедуры определения орбиты ИСЗ с помощью метода наименьших квадратов следующая.

1. Численно интегрируются уравнения движения (3.155) при начальных условиях Х(0) и определяется опорная орбита ИСЗ, а также компоненты 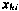вектора состояния 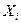, i=0, 1, 2, ..., N, для моментов 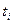, в которые производятся измерения.

2. На каждый момент 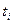, i—0, 1, 2,..., N, в который производят­ся измерения 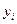, определяется расчетная дальность .

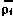3. Формируются разности 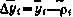. При этом предполагает­ся, что выборка 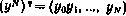известна. Одновременно иск­лючаются так называемые аномальные измерения, не удовлетворяющие условию

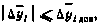
где 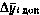— допустимое отклонение измерения от расчетного, ко­торое задается заранее из технических соображений.

4. Для моментов измерений 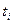, удовлетворяющих условию (3.165), вычисляются производные от координат 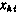текущего вектора состояния 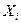по начальным условиям 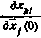, k,j=1, 2, …, 6; i=0, 1, 2, ..., N.

5. Рассчитываются частные производные 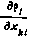от измеряемых параметров по компонентам x_ki вектора 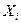и определяются значе­ния производных измеряемых параметров по начальным условиям .

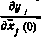6. Производится формирование нормальных уравнений .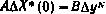

7. Решается система нормальных уравнений и определяются поправки к начальным условиям .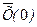

8. Формируется новый вектор начальных условий 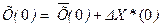, и решение задачи повторяется вновь с п. 1 до тех пор, пока на r-й итерации не будет выполнено условие

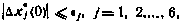
причем значение 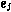задается заранее.

Система нормальных уравнений для определения вектора 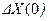может решаться либо путем обращения матрицы А, либо методом исключения с выбором главного элемента по столбцу матрицы А.

Ниже приводятся результаты имитационного моделирования процесса определения орбиты ИСЗ методом наименьших квадра­тов. Схема моделирования в ос­новном соответствует рис. 3.2. Исходные данные при моделирова­нии были приняты следующими. Параметры расчетной (опорной) орбиты ИСЗ: период Т = 22260 с, эксцентриситет е=0,75, наклоне­ние i = 63°, долгота восходящего узла 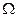= 84°. При этом экватори-

альные координаты ИСЗ на опорной орбите в момент t₀ равны 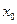= 892,2 км, 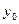= 9877 км, 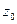= -1,46 км, 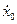= -2,82 км/с, 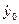= = 4,27 км/с, 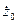= 6,25 км/с. Требовалось уточнить значения компо­нент вектора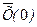 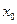, , 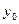, , 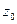, 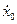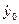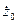при условии, что они заданы с априорными разбросами 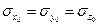= 0,5 км, 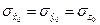= 20 м/с. В качестве измеряемого параметра принималась наклон­ная дальность до НИП, измеряемая со случайной ошибкой ), име­ющей среднеквадратичное отклонение 25 м. Число НИП варьирова­лось от одного до трех. Геодезические координаты НИП приведены в табл. 3.1.

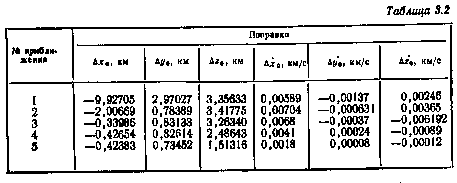
Результаты статистического моделирования приведены в табл. 3.2. В ней даны поправки к начальным условиям в зависимости от номера приближения при определении орбиты по данным трех НИП.

3.3.4. Аналитический алгоритм априорной оценки точности с использованиемметода наименьших квадратов

На основе метода наименьших квадратов может быть построен высокоэффективный с точки зрения быстроты вычисле­ний алгоритм оценки точности определения орбит ИСЗ, близких к круговым. Обычные методы, применяемые для оценки точности, весьма трудоемки, так как требуют вычисления либо баллистиче­ских производных (3.162), если применяется метод наименьших квадратов, либо использования рекуррентных соотношений вида (3.43), (3.44), (3.45) для апостериорной корреляционной матрицы расширенного вектора состояния оцениваемой динамической си­стемы, если для определения орбиты используется байесовский ал­горитм, например, фильтр Калмана или фильтр второго порядка. Для определения орбит измерения производятся на отдельных участках полета ИСЗ, определяемых, в частности, условиями ра­диовидимости ИСЗ, если измерения проводятся с НИПов. При этом на участках радиовидимости НИПы работают в течение огра­ниченных отрезков времени, называемых сеансами траекторных измерений. Поэтому представляет интерес алгоритм априорной

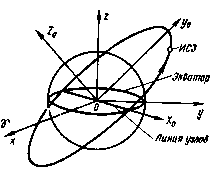
Рис. 3.16. Орбитальная наклонная сис­тема координат

оценки точности определения ор­биты, нерекуррентный по отноше­нию к отдельным измерениям в сеансе, а рекуррентный лишь по отношению к сеансам. Задача оце­нки точности определения орбиты ставится следующим образом. Требуется оценить точность опре­деления орбиты при заданном числе и расположении сеансов и НИП, заданных характеристиках точности измерения навигацион­ных параметров, заданных априорных разбросах орбиты и других условиях без определения непосредственно самих оценок вектора состояния ИСЗ. Иными словами, требуется определить лишь апос­териорные дисперсии компонент вектора состояния оцениваемой динамической системы.

В таком случае вопрос о сходимости оценок к истинным значе­ниям компонент вектора состояния не возникает и можно ограни­читься упрощенными моделями движения ИСЗ и траекторных из­мерений. Можно ограничиться, в частности, использованием лине­аризованной в окрестности опорной орбиты моделью движения ИСЗ. Решению линеаризованной в окрестности опорной экватори­альной орбиты системе уравнений соответствует фундаментальная матрица (3.77). Однако, когда опорная круговая орбита является наклонной, линеаризованная система уравнений движения не до­пускает решения в квадратурах. С целью устранения этой трудно­сти перейдем от экваториальной к орбитальной системе координат, начало которой совпадает с центром масс Земли, оси Ох_о и Оу_о лежат в плоскости опорной орбиты, ось Ох_о направлена в восходя­щий узел орбиты, ось Oz_o нормальна к плоскости орбиты и образу­ет правую тройку с осями Ох_о и Оу_о (рис. 3.16).

Введем в рассмотрение вектор состояния ИСЗ в сферических орбитальных координатах:

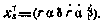
В таком случае, линеаризуя соотношения, связывающие вектор состояния 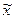ИСЗ в декартовой экваториальной системе координат с вектором 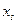, получаем

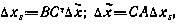
где

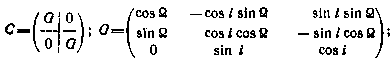
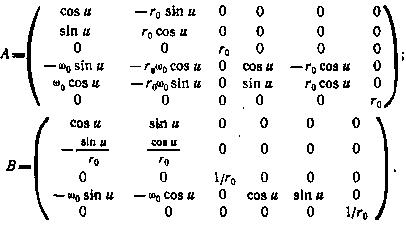
Здесь 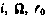— параметры опорной орбиты, 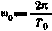- орбитальная угловая скорость ИСЗ; и — аргумент широты в опорном дви­жении.

В терминах компонент вектора 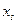можно определить фундамен­тальную матрицу линеаризованной системы уравнений движения ИСЗ. Формально эта матрица, которую обозначим 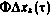, совпа­дает с фундаментальной матрицей (3.77).

Пусть расширенный вектор состояния ИСЗ в рассматриваемой задаче устроен так, как и вектор (3.73), с той лишь разницей, что рассматривается неуправляемое движение ИСЗ, так что ошибка реализации управляющего воздействия равна нулю. Поэтому в терминах линеаризованных уравнений движения ИСЗ имеем

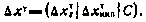
Считаем, что измеряемым параметром является наклонная даль­ность р.

В таком случае фундаментальная матрица, соответствующая вектору 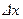, имеет вид

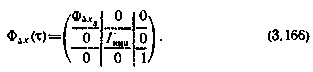
Нелинейное соотношение, связывающее измерения с вектором состояния оцениваемой системы, после линеаризации в окрестно­сти опорной орбиты принимает вид

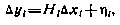
где 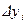— отклонение результата измерения от расчетного значе­ния измеряемого параметра, вычисленного на опорной орбите; H_i — матрица 1×10 вида

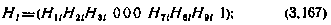
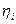- случайная ошибка измерений с характеристиками

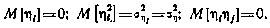
Предположим, что известна диагональная априорная корреля­ционная матрица расширенного вектора состояния 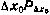. Эта корреляционная матрица может быть учтена при обработке изме­рений по методу наименьших квадратов, исходя из следующих со­ображений. Поскольку нас интересуют не оценки, а их апостери­орные дисперсии, можно условно считать, что наличие априорной корреляционной матрицы 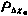10×10 эквивалентно проведению 10 дополнительных измерений дальности с точностью, характери­зуемой матрицей 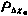. В таком случае матрица 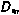, характеризу­ющая всю совокупность измерений в обрабатываемом сеансе, име­ет вид

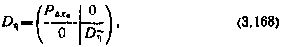
Где блок 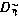представляет собой диагональную матрицу (N+ 1) × (N+ 1) с элементами .

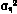Апостериорная корреляционная матрица вектора в резуль­тате обработки сеанса из (N+1) измерений согласно (3.147) при­мет вид

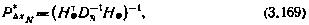
Где

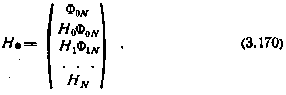
Соотношение (3.169) удобно записать в виде 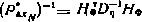, причем, учитывая структуру (3.167) матрицы Н и (3.166) матрицы 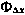, это выражение можно привести к виду

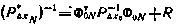
ИЛИ

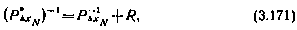
где R — матрица 10×10 вида

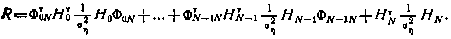
Таким образом, слагаемое R в правой части (3.171) отражает вклад измерений в уточнение оценок компонент вектора 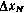. В ре­зультате приходим к следующей процедуре оценки точности, опи­сывающейся рекуррентными лишь по отношению к сеансам соотно­шениями:

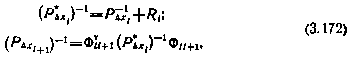
где i, i+1— номера сеансов; 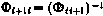— фундаментальная матрица вида (3.166), связывающая момент окончания предшест­вующего сеанса измерений с моментом начала очередного сеанса. Алгоритм расчета по соотношениям (3.172) существенно упро­щается, если предположить, что в пределах одного сеанса частные производные, входящие в матрицу Н, связывающую измеряемые и оцениваемые величины, не зависят от номера измерения, т. е. по­стоянны. В таком случае для элементов матрицы R записываются выражения достаточно простого вида:

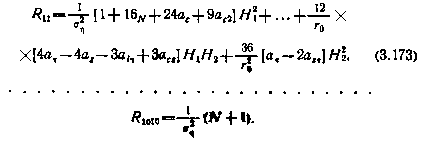
В этих выражениях (N+1) —число измерений в сеансе. Все элементы R₁₁,..., R₁₀₁₀ в конечном счете определяются девятью ко­эффициентами, которые могут быть рассчитаны заранее:

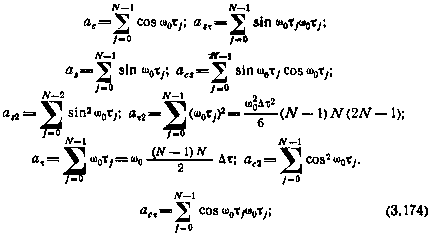
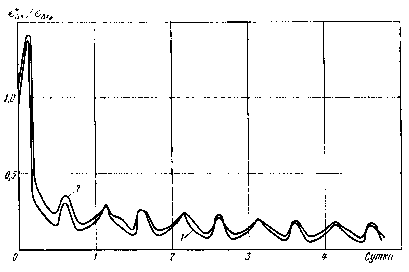
Рис. 3.17. Сравнение аналитического алгоритма и имитационного моделирования

Здесь 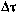— интервал между измерениями; 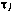— время от начала сеанса до j-го измерения.

Аналогичные выражения могут быть получены и для случая, когда измеряются два параметра: дальность р и скорость изменения дальности .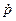

Эффективность рассмотренного алгоритма может быть показа­на на следующем примере. Пусть рассматривается задача оценки точности определения орбиты ИСЗ, находящегося на наклонной круговой 12-часовой орбите, по данным измерений дальности с трех НИПов.

На рис. 3.17 приведены кривые, показывающие результаты рас­четов оценки точности с помощью аналитического алгоритма (кривая 1) и рекуррентных соотношений фильтра Калмана (кри­вая 2). По оси абсцисс отложено время в сутках, а по оси ординат - нормированное cреднеквадратичное отклонение 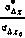- оценки компоненты 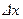вектора состояния ИСЗ. Здесь 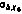- априорное среднеквадратичное отклонение компоненты. Рисунок де­монстрирует близость результатов, полученных различными мето­дами, при этом время проведения расчетов с помощью аналитического алгоритма примерно в 60 раз меньше.