Определение орбиты стационарного искусственного спутника Земли (СИСЗ) по данным наземных радиолокационных измерений с использованием фильтра Калмана

Под стационарным искусственным спутником Земли понимается спутник, движущийся в восточном направлении по круго­вой экваториальной орбите с периодом обращения, равным периоду собственного вращения Земли. Для наблюдателя, находящегося на Земле, СИСЗ будет казаться неподвижным. Благодаря этому свой­ству СИСЗ может быть использован для создания глобальной си­стемы связи и, в частности, системы непосредственного телевизион­ного вещания (системы НТВ).

Для обеспечения работоспособности системы НТВ орбиту СИСЗ необходимо периодически корректировать, так как вследствие не­точности вывода СИСЗ в рабочую, точку «стояния», а также вслед­ствие влияния аномалий и нецентральности гравитационного поля Земли СИСЗ будет «дрейфовать» относительно земного наблюда­теля. Кроме того, в процессе вывода СИСЗ на рабочую долготу «стояния» требуется неоднократная коррекция его орбиты. Процесс коррекции орбиты СИСЗ может быть реализован лишь в том случае, если известны параметры движения СИСЗ. Задача опреде­ления параметров движения СИСЗ может быть сформулирована следующим образом.

Требуется получить оптимальные оценки параметров движения СИСЗ по данным измерений, поступающих в дискретные моменты времени с наземных измерительных пунктов (НИП).

В качестве измеряемых или, как их принято называть, навига­ционных параметров рассмотрим наклонную дальность до СИСЗ и скорость ее изменения, а также косинусы направляющих углов ли­нии визирования. Для таких навигационных параметров движение СИСЗ удобно описывать в сферических координатах r, 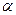, 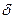(рис. 3.1). Здесь r — радиус-вектор СИСЗ, 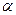— прямое восхожде­ние, т. е. угловое расстояние проекции радиус-вектора СИСЗ на экваториальную плоскость от направления на точку весеннего рав-нодействия 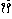; 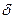— склонение, т. е. угловое расстояние СИСЗ от

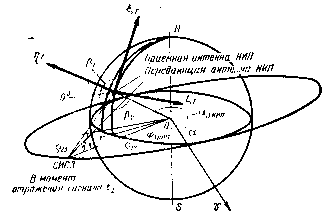
Рис. 3.1. К построению математической модели пространственного движения СИСЗ

плоскости экватора, отсчитываемое в меридиональной плоскости, содержащей спутник.

Случайными факторами, оказывающими влияние на движение СИСЗ, являются начальные ошибки вывода СИСЗ и ошибки реа­лизации управляющего воздействия. В качестве последнего рас­смотрим ускорение, создаваемое корректирующей двигательной установкой (КДУ), вектор тяги которой перпендикулярен радиус-вектору СИСЗ и параллелен экваториальной плоскости.

В сферических координатах уравнения движения СИСЗ в цен­тральном поле тяготения Земли имеют вид [29]

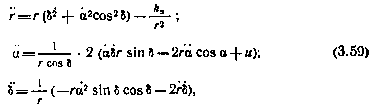
где и — управляющее ускорение; 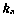— геоцентрическая гравитаци­онная постоянная.

Системе уравнений (3.59) соответствует вектор фазовых коор­динат 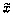с компонентами

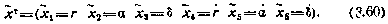
С учетом введенных обозначений система уравнений (3.59) в. нормальной форме принимает вид

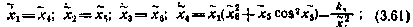
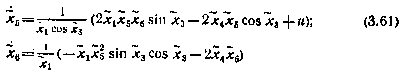
или в векторной форме

где 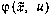—вектор-функция правых частей системы уравнений (3.61).

Начальные условия для (3.62): 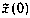—гауссовокий вектор с ма­тематическим ожиданием 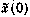и корреляционной матрицей .

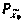Составим модель ошибок управляющего воздействия. Номиналь­ное значение тяги КДУ постоянно, однако истинное значение тяги определяется рядом случайных факторов, в частности, температу­рой и давлением рабочего тела и т. д. Поэтому тяга КДУ и, следо­вательно, управляющее ускорение представляют собой относитель­но медленно изменяющуюся функцию времени, случайным образом колеблющуюся относительно номинального значения.

На основании этого примем следующую модель управляющего ускорения:

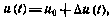
где 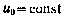— номинальное значение тяги; 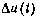— ошибка реали­зации управляющего воздействия, представляющая собой гауссов-ский стационарный процесс с нулевым математическим ожиданием и корреляционной функцией

Корреляционная функция (3.63) определяется двумя парамет­рами: 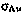— средним квадратичным отклонением ошибки реализа­ции управляющего ускорения и 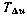— постоянной, характеризую­щей скорость изменения ошибки управляющего воздействия. Кор­реляционной функции (3.63) соответствует стохастическое диффе­ренциальное уравнение или уравнение формирующего фильтра пер­вого порядка [34]

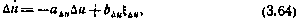
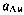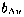где коэффициенты сноса и диффузии и однозначно определяются величинам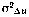и и 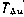по формулам

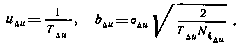
Здесь 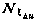— интенсивность белого шума. В реальной техниче­ской задаче не располагаем априорными значениям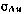и и 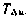. Бо­лее того, в реальной ситуации имеет смысл говорить не о значении T&U, определяющем скорость убывания корреляционной зависимости,

а об интервале корреляции тди, т. е. отрезке времени, за пределами которого значения процесса 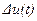считаются статистически незави­симыми с точностью, принятой в конкретной технической задаче.

В частности, если считать, что значения 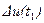и 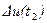корре-лированы, когда условная дисперсия 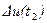при фиксированном значении 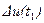составляет 99% от 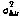, то значения 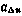и 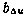опре­деляются по формулам, приведенным в [34]:

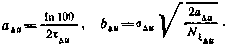
Из этих формул, в частности, следует, что при 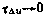марковский процесс 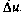, соответствующий стохастическому уравнению (3.64), превращается в белый шум, при 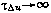— в постоянную в конкрет­ной реализации случайную величину, которой соответствует диф­ференциальное уравнение 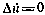. Начальное условие уравнения (3.64) — гауссовская случайная величина с нулевым математиче­ским ожиданием и дисперсией .

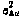Уравнения (3.62) и (3.64) образуют при условии, что 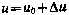и при заданных моментах включения и выключения КДУ, замкну­тую систему, описывающую управляемое движение СИСЗ.

Рассмотрим математическую модель измерений. Как уже ука­зывалось, с наземных измерительных пунктов измеряется суммар­ная наклонная дальность между НИП и СИСЗ, скорость измене­ния дальности, а также направляющие косинусы линии визиро­вания.

Положение передающей и приемной антенн НИП определяется вектором их геодезических координат на земном эллипсоиде: гео­дезической долготой 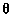и широтой антенны 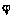, а также высотой ме­стоположения антенны над поверхностью земного эллипсоида Н. Положение передающей антенны относительно приемной считаем известным точно. Таким образом, привязка НИП к местности ха­рактеризуется величинами 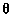, 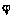и Н — компонентами вектора геоде­зических координат одной из антенн НИП, например, приемной. В общем случае привязка НИП к местности неточная. Иначе гово­ря, вектор геодезических координат приемной антенны НИП слу­чайный. Считаем, что компоненты этого вектора распределены по нормальному закону с известными априорными характеристиками. Положение НИП, вообще говоря, может быть уточнено в процессе определения орбиты СИСЗ. Обозначим вектор геодезических коор­динат НИП

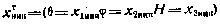
и включим его в число компонент расширенного вектора состояния, поставив ему в соответствие формальное дифференциальное урав­нение формирующего фильтра 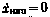с начальными условиями 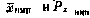, представляющими собой параметры априорного рас­пределения вектора

Построим теперь непосредственно модель измерений, т. е. ус­тановим зависимость между измеренными величинами, компонен­тами вектора состояния СИСЗ и геодезическими координатами ан­тенны НИП.

Суммарная измеряемая дальность 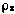образуется ломаной лини­ей: передающая антенна — СИСЗ — приемная антенна. При этом значение дальности 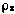определяется положением трех точек: пере­дающей антенны в момент излучения сигнала 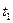,СИСЗ в момент отражения им радиосигнала 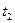и приемной антенны в момент при­хода на нее отраженного радиосигнала 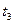, т. е.

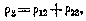
где 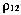— расстояние между СИСЗ в момент 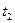и точкой, в которой находилась передающая антенна в момент 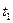; 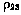— расстояние меж­ду приемной антенной в момент 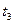и точкой, в которой находился СИСЗ в момент 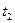. Скорость изменения дальности условно привя­зывается к моменту 4-

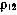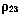Определим явную зависимость и от компонент вектора состояния СИСЗ и геодезических координат НИП.

Обозначим компоненты вектора геодезических координат пере­дающей антенны 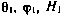; приемной— 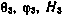. Тогда, рассмат­ривая Землю как эллипсоид вращения, можем записать, следуя [29]

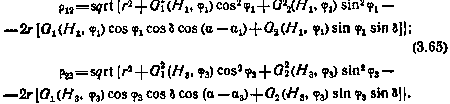
В выражениях (3.65) радиус-вектор СИСЗ r, склонение СИСЗ 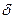и прямое восхождение СИСЗ 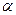соответствуют моменту t₂, кроме того,

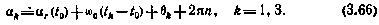
Здесь 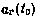— прямое восхождение гринвичского меридиана на мо­мент начала процесса определения орбиты 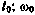— угловая скорость Земли; целое п выбирается из условия

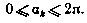
формулах (3.65) введены также следующие обозначения:

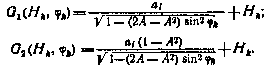
Здесь 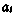— экваториальный радиус Земли; А—сжатие земного эл­липсоида.

Вследствие конкретных особенностей измерительных систем фактически известны не р₁₂ и р₂₃, а лишь значение 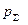и момент t₃, к которому это значение условно привязывается (в дальнейшем момент t₃будем называть расчетным моментом измерения). Поэто­му для определения р₁₂ и р₂₃ используется специальная процедура, существо которой состоит в следующем.

Пусть величины р₁₂ и р₂₃ известны. Тогда можно написать

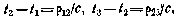
где с — скорость распространения радиоволн. Так как р₁₂ и р₂₃ яв­ляются функциями t₁, t₂ и t₃, то, поскольку результаты измерений привязываются к моменту t₃, можно определить моменты t₁ и t₂ и, следовательно, р₁₂ и р₂₃ путем последовательных приближений.

Моменты t₂ и р₂₃ определяются соотношениями

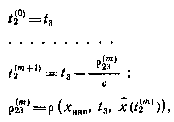
где т — номер приближения; 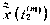— сценка вектора 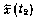, про­гнозируемая к моменту 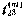из предшествующего расчетного момен­та измерения. Значение 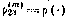рассчитывается каждый раз по соответствующей формуле (3.65).

Если момент t₂ определен, то t₁ и р₁₂ определяются следующие образом:

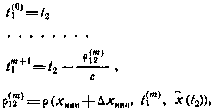
где 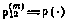рассчитывается по соответствующей формуле (3.65), а 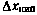— известный вектор смещения геодезических координат пе­редающей антенны НИП относительно приемной.

Запишем теперь выражение, определяющее зависимость скоро­сти изменения суммарной дальности, 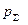от компонент вектора 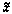, рассматривая моменты t₁ и t₃ как параметры, от которых также зависит суммарная дальность :

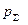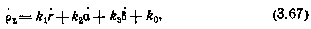
где

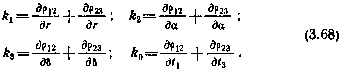
Подробные выражения для соответствующих частных производных р₁₂ и р₂₃ по компонентам вектора состояния СИСЗ, параметрам t₁ и t₃ приведены в [34].

Значения компонент вектора состояния 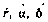в(3.67) и значе­ния соответствующих частных производных в (3.68) отнесены к моменту t₂.

Используя результаты, приведенные в [34], запишем выражения, определяющие направляющие косинусы линии визирования СИСЗ как функции компонент векторов 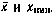. При этом углы 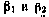(см. рис. 3.1) определяются как углы между линией, соединяющей СИСЗ в момент t₂ и приемную антенну НИП в момент t₃, и осями так называемой топоцентрической системы координат 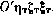. Начало этой системы координат совпадает с приемной антенной, ось 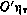направлена по нормали к поверхности земного эллипсоида, ось 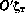принадлежит плоскости меридиана и направлена на север, ось 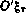образует с двумя другими осями правую систему коорди­нат. С учетом этого имеем

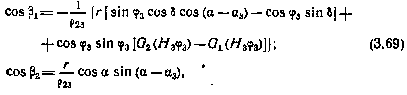
где определяются выражениями (3.65) и (3.66); 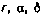со­ответствуют моменту t₂.

Результаты измерений искажаются ошибками, содержащими две статистически независимые составляющие:

1) быстроменяющиеся ошибки, представляющие собой дискрет­ную последовательность статистически независимых гауссовских случайных величин с нулевым математическим ожиданием и извест­ной корреляционной матрицей. Если обозначить вектор таких оши­бок, относящихся к некоторому расчетному моменту t_i, через 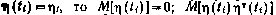— диагональная матрица с элементами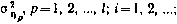

2) относительно медленно меняющиеся (систематические) ошибки 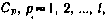сопровождающие измерение какой-либо из величин 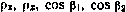. Эти ошибки образуют вектор размер­ности l×l. В качестве математической модели систематических ошибок можно принять гауссовский случайный процесс, корреля­ционная функция которого

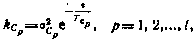
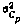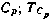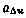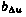где —априорная дисперсия ошибки —постоянная, ха­рактеризующая скорость убывания корреляционной зависимости. Этой корреляционной функции соответствует стохастическое дифференциальное уравнение формирующего фильтра первого по­рядка вида (3.64). Значения коэффициентов этого формирующего фильтра определяются аналогично значениям коэффициентов и формирующего фильтра для ошибки реализации управляющего воздействия 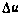. Вектор систематических ошибок С удовлет­воряет стохастическому уравнению

где Ас, В_с — матрицы l×l коэффициентов 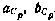, определяемых аналогично коэффициентам 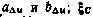— вектор белых шумов с матрицей интенсивности 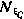. Начальные условия для уравнения (3.70): С(0) — гауссовский вектор с характеристиками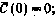 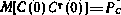— диагональная матрица с элементами , .

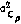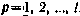В соответствии с приведенными выше моделями измерений в каждый расчетный момент проведения измерений 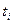формируется вектор измерений

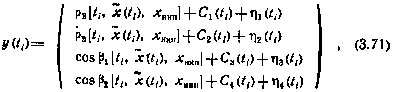
или

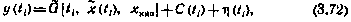
где 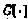— вектор-функция зависимостей, определяемых с помощью (3.65), (3.67), (3.68), (3.69).

Состав расширенного вектора состояния, подлежащего оценива­нию в данной задаче

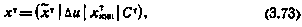
в том числе: первые шесть компонент, образующие вектор 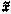, харак­теризуют координаты и скорость СИСЗ; седьмая компонента 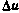— ошибка реализации управляющего воздействия; следующие три компоненты, образующие вектор , характеризуют положение НИП, и наконец, четыре компоненты—систематические ошибки, образующие вектор С — всего 14 компонент. Этот вектор удовлетво­ряет стохастическому дифференциальному уравнению

где

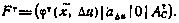
Здесь 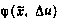определяется выражением (3.61), В – блочная матрица 14x5, имеющая структуру

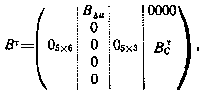
где 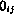— нулевые блоки соответствующих размерностей; .

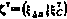Начальные условия для уравнения (3.74) —гауссовский вектор х(0) с характеристиками

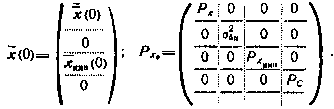
С учетом введенных обозначений выражение для вектора изме­рений (3.72) можно переписать в виде

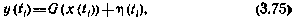
где

Модели состояния (3.74) и измерений (3.75) вследствие их нели­нейности непосредственно непригодны для использования в линей­ном рекуррентном алгоритме оценивания, каким является фильтр Калмана. С целью получения приемлемых моделей уравнения (3.74) и соотношения (3.75) следует линеаризовать в окрестности некоторого опорного движения. Здесь в качестве опорного естест­венно принять движение спутника по стационарной орбите в цент­ральном поле тяготения при отсутствии управляющего ускорения. В результате линеаризации в окрестности опорной стационар­ной орбиты система уравнений (3.74) становится линейной с посто­янными коэффициентами. Фундаментальная матрица, соответствую­щая этой системе уравнений, устроена следующим образом:

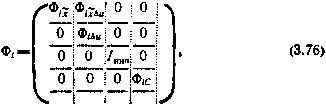
тде — фундаментальная матрица линейной однородной системы уравнений, получающейся в результате линеаризации системы урав­нений (3.61); — блок-столбец 6×1, учитывающий случайный разброс управляющего воздействия; блок 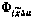образуется на осно­ве частного решения линейной системы уравнений, получающейся в результате линеаризации системы уравнений

—фундаментальное решение уравнения (3.64); 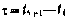— интер­вал между двумя соседними моментами времени, в которые рас­сматривается состояние СИСЗ, например, интервал между момен­тами измерений; 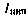— единичная матрица 3×3, представляющая собой фундаментальную матрицу для дифференциального уравне­ния 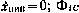— фундаментальная матрица уравнения (3.70) при l = 4.

Рассмотрим теперь блоки фундаментальной матрицы (3.76) подробнее.

Фундаментальная матрица при линеаризации уравнений (3.61) в окрестности стационарной орбиты может быть определена аналитически, например, с помощью операционного исчисления. Соответствующие выражения приведены в [34] и имеют вид

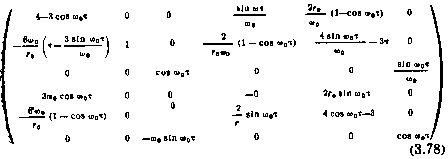
Здесь — параметры опорной орбиты; 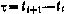— имеет ■тот же смысл, что и в (3.77). Состав элементов блока 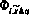следу­ющий:

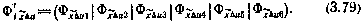
Элементы этого блока могут быть определены в явном виде лишь путем численного интегрирования. В частности, для определения 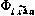можно воспользоваться методом конечных разностей:

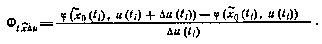
В этой формуле 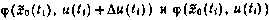— резуль­таты численного интегрирования системы уравнений (3.62) на отрезке 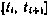при начальных условиях 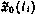и управлении 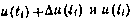соответственно.

Фундаментальная матрица 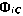также определяется аналитиче­ски:

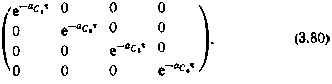
Соотношения .(3.75) также должны быть приведены к линейно­му виду

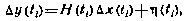
где 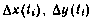— отклонения векторов 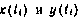от их значе­ний, соответствующих движению СИСЗ по опорной орбите.

Опуская в этой формуле для простоты записи аргументы, полу­чаем

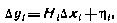
где H_i — матрица частных 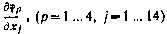, элементы которой вычислены для стационарной (опорной) орбиты. В соответствии с выражениями (3.65), (3.67), (3.69), входящими а вектор-функцию 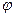, и составом расширенного вектора состояния х (3.73) матрица H_i, устроена следующим образом:

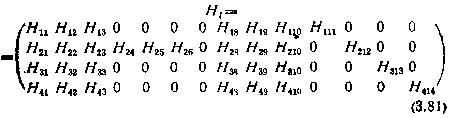
Элементы H_Pj(p=1, ..., 4, _j=l, ..., 14) матрицы H_i могут быть вычислены аналитически с использованием выражений (3.65) — (3.69) либо с помощью этих же выражений численно, методом ко­нечных разностей, подобно тому как вычислялись элементы блока 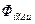. Выражения для элементов матрицы H_i, полученные аналити­чески, весьма громоздки и поэтому здесь в явном виде не приво­дятся.

Таким образом, матрицы 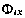и H_i определены полностью. Фор­мулы фильтра Калмана справедливы лишь для линейной системы, в то время как в рассматриваемой технической задаче имеем дело с линеаризованной динамической системой. Это означает, что соотно­шения (3.13) и (3.17) в данной технической задаче выполняются

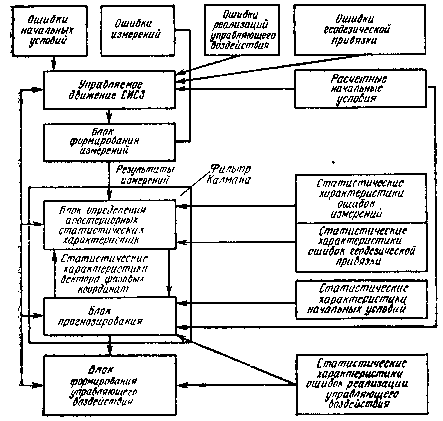
Рис. 3.2. Схема имитационного моделирования

приближенно, с точностью до ошибок линеаризации. В результате применения соотношений линейного фильтра Калмана к линеари­зованной системе может возникнуть эффект, называемый «расхо­димостью» или «неустойчивостью» фильтра Калмана. Сущность этого эффекта состоит в том, что апостериорные дисперсии, харак­теризующие точность оценивания компонент вектора , рассчиты­ваемые по формулам (3.43) и (3.44), уменьшаются, в то время как значения оценок компонент векторов 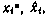рассчитываемые по формулам (3.42) и (3.45), все более отличаются от истинных зна­чений этих компонент.

С целью выявления этого эффекта и его устранения путем соот­ветствующих модификаций линейного фильтра Калмана, рассмат­риваемых ниже, как правило, проводят имитационное моделирова­ние процесса оценивания.

Схема имитационного моделирования приведена, на рис. 3.2. Приведем некоторые типичные значения исходных данных, исполь­зуемых при подобном имитационном моделировании.

1. Оскулирующие элементы опорной орбиты: период Т=86 164 с, эксцентриситет е = 0,005, наклонение i = 0,03, долгота восходящего узла 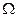= 1,3, аргумент широты 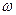= 0,4, истинная аномалия 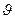= 4,3.

2. Априорная корреляционная матрица Р_о, как правило, прини­мается диагональной со среднеквадратичными отклонениями:

\

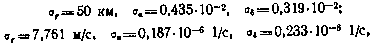что соответствует априорному среднему квадратичному отклонению периода обращения от расчетного 850 с.

3. Параметры корреляционной функции систематических ошибок измерений и ошибки реализации управляющего воздействия выби­раются таким образом, чтобы соответствующие уравнения форми­рующих фильтров были формальными, т. е. С = 0, что соответствует интервалу корреляции, равному бесконечности.

4. Среднеквадратические отклонения быстро меняющихся оши­бок измерения берутся, как правило, равными соответствующим априорным среднеквадратичным отклонениям систематических оши­бок, которые, в свою очередь, равны [20], [34]:

по дальности 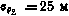, по скорости изменения дальности 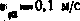, по направляющим косинусам линии визирования .

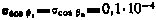5. Априорное среднеквадратичное отклонение ошибки реализа­ции управляющего воздействия .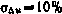

6. Интервал между измерениями 5 с.

7. Интервал времени (мерный участок), на котором проводится моделирование, принимается равным Т = 24 час.

8. Максимальное время работы КДУ—1 ч.

Результаты моделирования представлены на рис. 3.3. Эти ри­сунки характеризуют результаты оценивания при пассивном движе­нии СИСЗ (u = 0, Δu = 0) для тех реализаций, когда фактические отклонения начальных условий от расчетных примерно равны сред­неквадратичным отклонениям. Отклонения оценок от истинных значений компонент уменьшаются со временем, однако можно от­метить значительные выбросы ошибок оценивания. При наличии ошибок реализации управляющего воздействия и при отклонениях фактических начальных условий от расчетных, близких к предель­ным, проявляется «неустойчивость» фильтра Калмана, характерный пример которой для компоненты а приведен на рис. 3.4.

3.2.3. Применение фильтра Калмана для начальнойвыставки инерциальной навигационной системы беспилотного летательного аппарата

Под начальной выставкой инерциальной навигационной системы (ИНС) понимается процесс согласования ориентации осей системы координат, реализуемой с помощью гиростабилнзирован-ной платформы (ГСП) ИНС, с осями некоторой эталонной (базо-

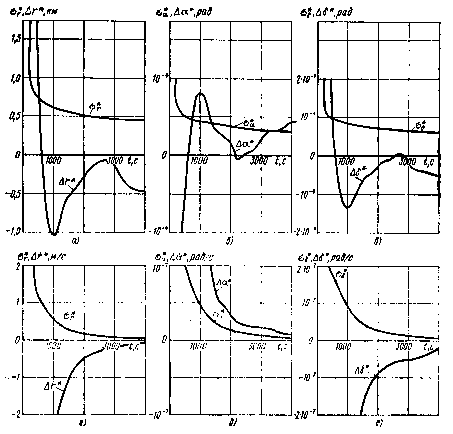
Рис. 3.3. Имитационное моделирование с использованием фильтра Калмана:

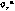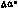а — ошибка оценки и апостериорное среднеквадратичное отклонение радиус-вектора r СИСЗ; — ошибка оценки и апостериорное среднеквадратичное отклонение 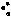прямого восхождения СИСЗ; в — ошибка оценки 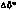и апостериорное среднеквадратичное отклонение 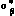склонения СИСЗ; г — ошибка оценки 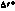и апостериорное среднеквадратич­ное отклонение 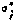скорости измерения радиус-вектора СИСЗ 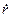; д — ошибка оценки 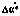и апостериорное среднеквадратичное отклонение 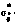скорости изменения прямого восхожде­ния СИСЗ 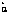; е — ошибка оценки 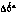и апостериорное среднеквадратичное отклонение 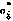скорости измерения склонения СИСЗ .

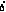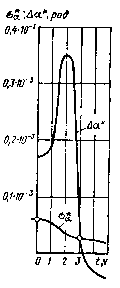Рис. 3.4. Пример расходимости оценок при использова­нии фильтра Калмана

вой) системы координат, реализуемой, например, с помощью ГСП некоторой эталонной ИНС.

Кроме того, при выставке осуществляют оценку угловых скоро­стей уходов (дрейфа) гироскопов, реализующих инерциальную си­стему координат как для выставляемой, так и для эталонной ИНС.

Процесс определения этих оценок принято в подобных задачах называть комплексной обработкой информации. Целью такой обработки является повышение точности определе­ния состояния беспилотного ЛА ,и носителя.

-В рассматриваемой задаче в качестве эта­лонной ИНС может использоваться ИНС но­сителя беспилотного ЛА. В свою очередь, ИНС носителя выставляется с помощью датчиков внешней информации, например, с помощью радиодальномеров и доплеровских измерите­лей скорости (ДИС). Выставка ИНС беспилот­ного ЛА (ИНС ЛА) по ИНС носителя (ИНС Н) осуществляется на борту носителя, причем должна осуществляться выставка одновремен­но нескольких ИНС беспилотных ЛА, находя­щихся либо в фюзеляже носителя, либо подве­шенных под его крыльями, в условиях интен­сивной вибрации.

В этих условиях выставка ИНС ЛА по данным ИНС Н может быть успешно осущест­влена с помощью линейного дискретного филь­тра Калмана. Как уже говорилось, одновременно с выставкой осу­ществляется вычисление оценок компонент расширенного вектора состояния ЛА, включающего, помимо составляющих положения и скорости ЛА, различного рода аппаратурные ошибки ИНС ЛА. В процессе коррекции данных ИНС Н по данным датчиков внеш­ней информации также осуществляется вычисление оценок аппара­турных ошибок ИНС Н.

Рассмотрим математическую модель движения носителя, ис­пользуемую для комплексной обработки информации при началь­ной выставке ИНС ЛА. В процессе выставки используются два фильтра Калмана: один для обработки информации, поступающей от радиолокационного измерителя дальности и ДИС, и другой — для обработки информации, поступающей от ИНС носителя. Расши­ренные векторы состояния носителя и ЛА, оценки которых получают с помощью фильтров Калмана, имеют разную размерность.

Расширенный вектор состояния носителя х_н включает следую­щие 14 компонент:

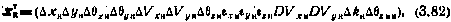
Здесь 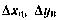—отклонения компонент вектора х_н, характери­зующих положение носителя по данным, получаемым от ИНС Н, по осям О₀Х_с и O,₀Y_c стартовой системы координат, от соответст­вующих значений, определяемых с помощью радиолокационной станции (РЛС) носителя.

Стартовая система координат определяется следующим обра­зом: направление оси О₀Х_с определяется азимутом запуска 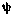(ази­мут— угол между направлением на север и направлением полета)

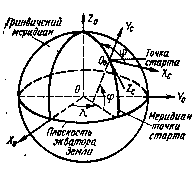
Рис. 3.5. Стартовая система координат

относительно меридиана точки стар­та. Ось O₀Y_c направлена вверх по прямой, проходящей через центр Земли и точку старта О₀; ось O_QZ_C дополняет систему до правой (рис. 3.5). На этом рисунке 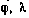— широта и долгота точки старта.

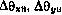— отклонения углов, оп­ределяющих направление местной вертикали по данным ИНС Н, от со­ответствующих углов по данным РЛС носителя.

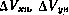— отклонения составляющих скорости, определенных по данным ИНС Н, от соответствующих составляющих, получаемых по данным ДИС. Компоненты отсутствуют, так как ка­нал z использует информацию от баровысотомера и здесь не рас­сматривается.

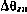— рассогласование, измеренное в азимутальной плоскости, между истинным значением азимута и азимутом, материализуемым с помощью гиростабилизированной платформы ИНС Н. 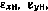, 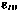— угловые скорости ухода гироскопов ИНС Н по осям О₀Х_с, O₀Y_c и O₀Z_c соответственно.

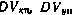— систематические ошибки определения скорости с помощью