Предельные возможности оптимального кодирования

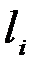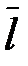Определим границы для и б пользуясь эвристическими соображениями, основанными на количестве информации. Очевидно, код будет самым экономным, если каждый символ кодового слова будет переносить максимально возможное количество информации.

Поскольку собственное количество информации, содержащееся в сообщении 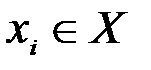, равно 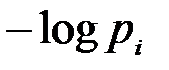информационной емкости соответствующего кодового слова будет достаточно, чтобы перенести указанное количество информации, только в том случае, если его минимальная длина l_i будет находиться в пределах 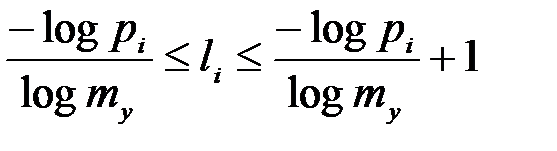, где 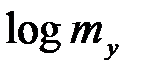- максимальное количество информации, которое может перенести отдельный символ кодового слова.

Усредняя неравенство по всему множеству X сообщений, получим неравенство, определяющее границы для минимальной средней длины кодового слова: .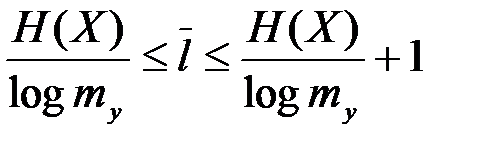

В данном случае довольно большой интервал изменения возможных значений 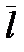. Однако при кодировании блоков (слов из n букв x_i) средняя длина 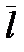приближается к значению 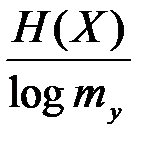при неограниченном увеличении длины блока п, что следует из неравенства 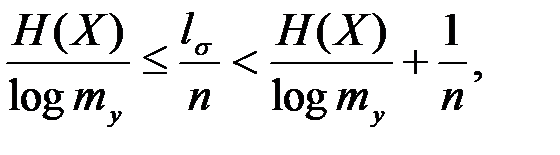где 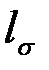- среднее количество символов кодового слова, приходящееся на один блок, а 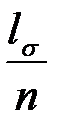на одну букву в блоке.

Полученные неравенства справедливы для всех однозначно декодируемых кодов.

Алгоритмы эффективного кодирования

Алгоритм Шеннона-Фано.

Пусть имеется множество сообщений .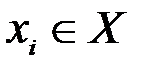

1. Все сообщения располагаются в порядке убывания их вероятностей.

2. Упорядоченное множество сообщений делится на две части: верхнюю часть и нижнюю часть, причем так, чтобы разность между суммой вероятностей в верхней и нижней части была минимальной.

3. После этого сообщениям в верхней части ставится в соответствие 1, а в нижней – 0.

4. Далее аналогичные действия производятся с каждой из частей. Вновь полученные подмножества сообщений снова аналогичным образом делятся на две части и т.д., до получения по одному сообщению в каждом из подмножеств.

5. В результате каждому сообщению будет соответствовать своя последовательность из нулей и единиц, т.е. кодовое слово.

Пример:

Таблица 4.3

pi	X
0.5	x1
0.25	x2
0.125	x3
0.125	x4

Алгоритм Хаффмена.

1. Все сообщения располагаются в порядке убывания их вероятностей.

2. Два самых нижних сообщения объединяются в одно событие, вероятность которого равна сумме вероятностей, объединяемых событий, причем верхнему событию ставится в соответствие 1, а нижнему 0.

3. Получился новый массив сообщений с количеством состояний на единицу меньшим по сравнению с предыдущим массивом, если два последних события считать одним более крупным событием. Далее преобразуем этот массив в соответствии с пунктами 1 и 2. Полученный массив вновь подвергаем указанным преобразованиям и т.д. до тех пор, пока не будет исчерпан весь массив.

4. Геометрически результат можно представить в виде дерева, где кодовое слово, соответствующее 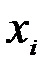выражается последовательностью ветвей с соответствующим сообщением .

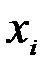Пример:

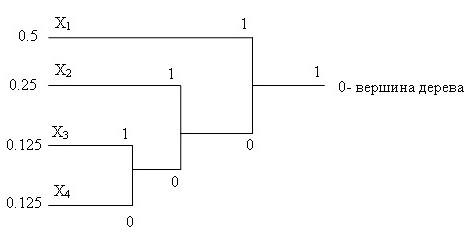
x₁=1, x₂ = 01, x₃ = 001, x₄ = 000

Рис. 4.3. Геометрическая интерпретация алгоритма Хаффмана