Собственное количество информации и энтропия

Пусть в канале отсутствуют помехи. Тогда между элемен­тами множеств X и У имеет место взаимно однозначное соответствие и p(x_i|y_j)=1 при j=i. В этих условиях количество информации, которое y_j (j=i) доставляет об x_i, согласно (4.3) равно .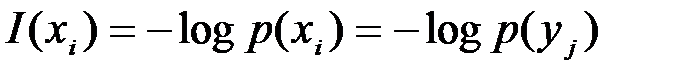

Эта величина называется собственным количеством информации, которое несет символ x_i, причем всегда I(x_i)>0. Усредняя I(x_i) по всему множеству x_i, получим количество информации, которое в среднем несут сообщения множества X. Среднее значение совпадает с энтропией

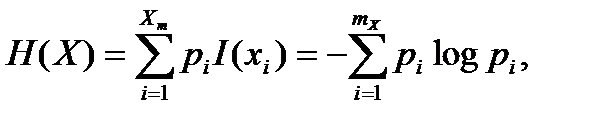
где p_i=p(x_i).

Взаимная информация

Источник информации и приемник можно рассматривать как подсистемы одной сложной системы. Взаимную информацию между состояниями подсистем, используя (4.3), можно записать в виде

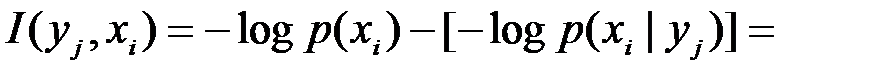
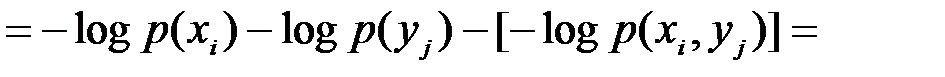
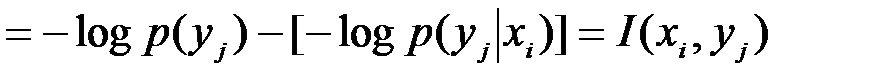. (4.4)

Поскольку сложная система случайным образом приходит в то или иное состояние, определяемое парой чисел (x_i,y_j), то I (xi,y_j) будет случайной величиной, которую можно усреднить по всему множеству состояний. В результате почленного усреднения (4.4) получим выражение для средней (полной) взаимной информации:

,

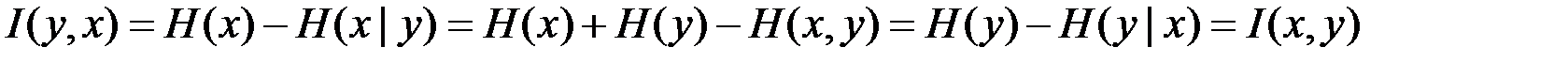(4.5)

где I(y,x)=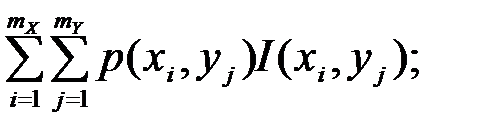

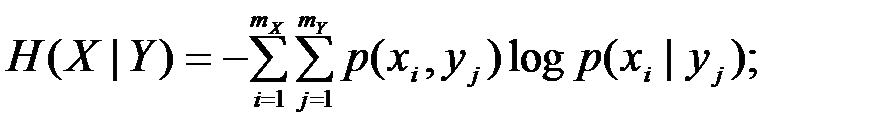
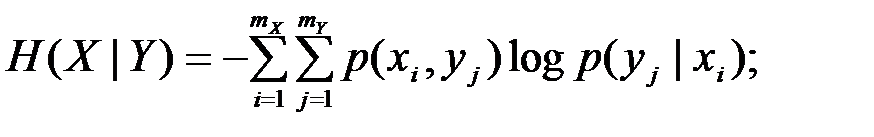
С точки зрения информационного описания системы связи безразлично, какую из подсистем рассматривать в качестве передатчика, а какую в качестве приемника.

Поэтому энтропии Н(Х) и H(У) можно интерпретировать как информацию, которая поступает в канал связи, а условные энтропии H(X|Y), H(Y|X) как информацию, которая рассеивается в канале. В [1] доказано, что I(Х, У)≥0.

При выполнении указанного неравенства из (4.5) следует, что

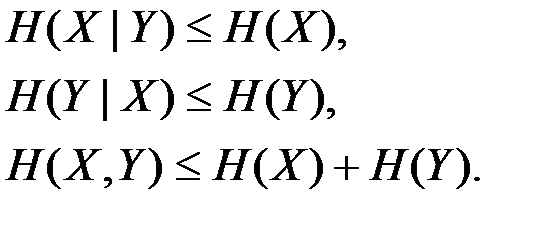
Условную энтропию можно представить в виде

,

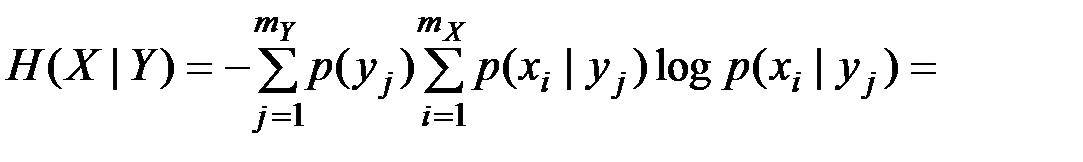
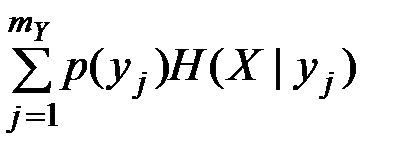где величина 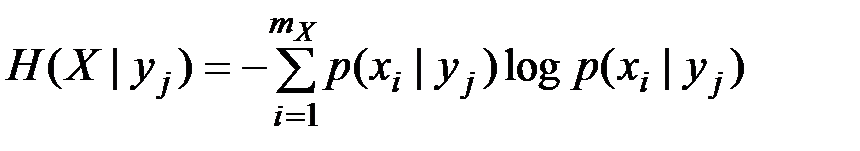называется частной условной энтропией. Она характеризует неопределенность состояния системы А в случае, когда известно состояние y_j наблюдаемой системы В. Зафиксировав состояние y_j системы В, мы тем самым изменяем комплекс условий, при которых может реализоваться событие x_i. Это обнаруживается как изменение вероятности реализации события x_i (i= 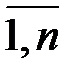) (имеет место статистическая зависимость). Если до изменения условий указанная вероятность была равна безусловной (полной) вероятности p(X_i), то после изменения условий она стала равной условной вероятности p(x_i|y_j). При отсутствии статистической зависимости H(X|y_j)=H(X), поскольку P(x_i|y_j)=p(x_i).

Таблица 4.1

x y	x1	x2	p(yj)
y1 y2	0.5 0.25	0.25	0.5 0.5
p(xi)	0.75	0.25

Таблица 4.2

x y	x1	x2
y1 y2	0.5	0.5

При наличии статистической зависимости энтропия H(X|y_j) может оказаться как меньше, так и больше Н(Х). Напомним, что для энтропии H(X|Y) всегда справедливо неравенство H(X|Y)≤H(X).

В качестве примера вычислим энтропии Н(Х), H(X|Y), H(X|y_j) и взаимную информацию I(Х,У), когда системы А и В описываются двумерным распределением p(x_i, y_j), заданным в виде табл. 1.

Вычисленные значения условной вероятности 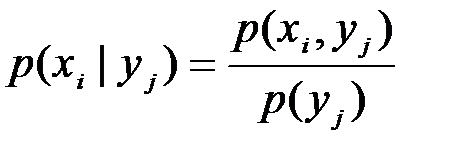записаны в табл. 4.2.

Используя записанные в таблицах значения вероятностей, получим

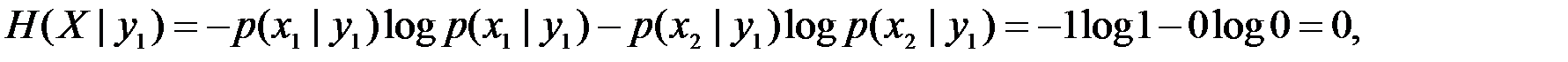
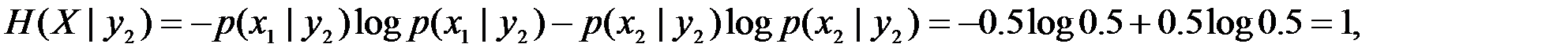
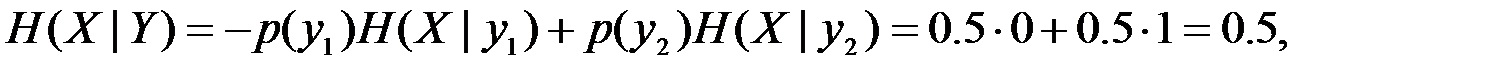
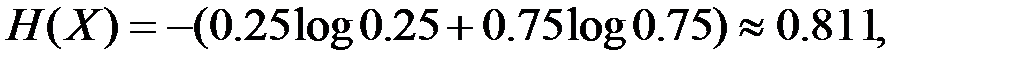
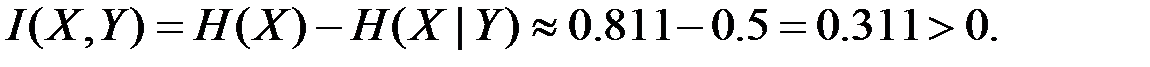
Отсюда

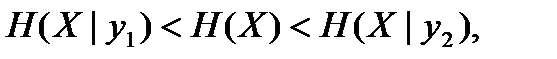
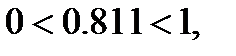
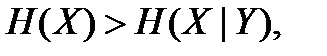
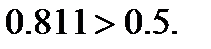
ДИСКРЕТНЫЕ ИСТОЧНИКИ СООБЩЕНИЙ И

ИХ ОПИСАНИЕ

Эргодические источники

Источник будем называть эргодическим, если его вероятностные параметры можно оценить по одной достаточ­но длинной реализации, которую он вырабатывает. При неограниченном возрастании длины реализации (n) оценка параметра (результат измерения) совпадает с его истинным значением с вероятностью, равной единице. Например, при бросании игральной кости можно оценить вероятность выпадания какой-либо цифры через относительную частоту ее появления в достаточно длинной серии испытаний. Указанная серия испытаний представляет собой ту самую реализацию, по которой осуществляется оценка вероятности (параметра). Реализации, по которым можно оценить закон распределения, являются типичными. Поэтому эргодическим источником можно назвать источник, который вырабатывает типичные последовательности. Типичная последовательность несет сведения о структуре источника, то есть является типичной для данного источника. Если два источника различаются своей структурой (значением оцениваемого параметра), то, наблюдая реализацию, можно определить, какому из них она принадлежит. Источник, эргодический по одному параметру, может оказаться не эргодическим по другому параметру.