Метод максимального правдоподобия
Вид любого закона распределения 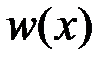 зависит только от комплекса условий D, изменение которого, вызванное изменением значения некоторого параметра
зависит только от комплекса условий D, изменение которого, вызванное изменением значения некоторого параметра 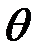 , может привести к изменению вида закона распределения
, может привести к изменению вида закона распределения 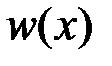 . В этом случае параметр
. В этом случае параметр 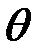 можно рассматривать как параметр закона распределения
можно рассматривать как параметр закона распределения 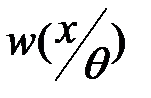 случайной величины
случайной величины 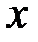 . Необходимо получить оценку
. Необходимо получить оценку 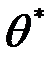 значения параметра
значения параметра 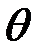 при условии, что тип закона распределения известен, но при этом не известно значение его параметра. Оценка параметра
при условии, что тип закона распределения известен, но при этом не известно значение его параметра. Оценка параметра 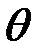 производится на основе выборки
производится на основе выборки 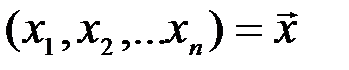 , которая представляет собой последовательность из
, которая представляет собой последовательность из 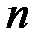 результатов испытаний при неизвестном, но одном и том же значении параметра
результатов испытаний при неизвестном, но одном и том же значении параметра 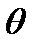 . В качестве оценки выбирается такое значение параметра, которое чаще всего появляется при полученной в результате опыта выборке. Это значение называется оценкой по максимуму апостериорной (послеопытной) вероятности и вычисляется как
. В качестве оценки выбирается такое значение параметра, которое чаще всего появляется при полученной в результате опыта выборке. Это значение называется оценкой по максимуму апостериорной (послеопытной) вероятности и вычисляется как 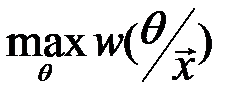 . К сожалению, на практике возникают проблемы с определением вида функции
. К сожалению, на практике возникают проблемы с определением вида функции 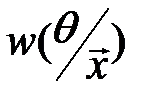 и поэтому чаще всего пользуются правдоподобной оценкой, которая строится следующим образом. Параметр
и поэтому чаще всего пользуются правдоподобной оценкой, которая строится следующим образом. Параметр 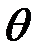 и выборку
и выборку 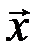 можно рассматривать как две зависимые случайные величины с двухмерным законом распределения
можно рассматривать как две зависимые случайные величины с двухмерным законом распределения 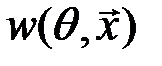 , причем
, причем 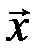 принадлежит выборочному пространству, а
принадлежит выборочному пространству, а 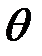 пространству параметров. По формуле умножения вероятностей имеем:
пространству параметров. По формуле умножения вероятностей имеем: 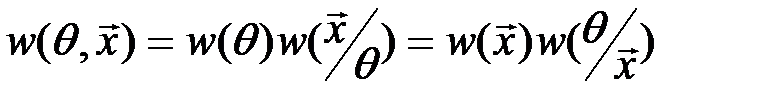 . Отсюда следует, что
. Отсюда следует, что 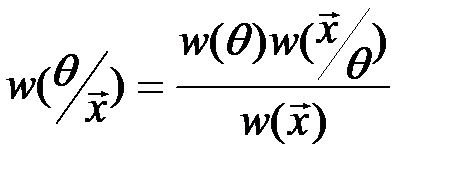 , где
, где 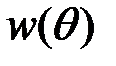 - априорный (доопытный) закон распределения параметра
- априорный (доопытный) закон распределения параметра 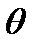 .
.
Если параметр 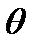 подчиняется равномерному закону распределения, то
подчиняется равномерному закону распределения, то 
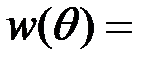 const на пространстве параметров и функции
const на пространстве параметров и функции 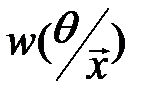 и
и 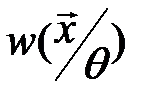 достигают своего максимального значения при одном и том же значении параметра
достигают своего максимального значения при одном и том же значении параметра 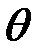 . В этом случае функция
. В этом случае функция 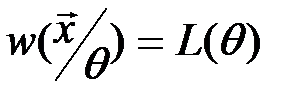 называется функцией правдоподобия и обозначается как
называется функцией правдоподобия и обозначается как 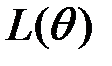 , а значение параметра
, а значение параметра 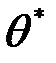 , которое доставляет максимум функции правдоподобия
, которое доставляет максимум функции правдоподобия 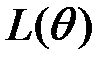 , называется правдоподобной оценкой. Следует напомнить, что выборка
, называется правдоподобной оценкой. Следует напомнить, что выборка 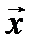 постоянна в процессе вычисления оценки параметра.
постоянна в процессе вычисления оценки параметра.
Пример. Вычислить оценки максимального правдоподобия для дисперсии и математического ожидания гауссова закона распределения 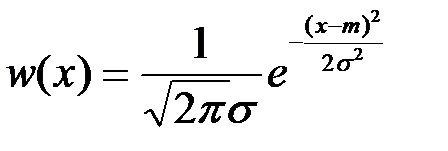 .
.
Решение. Поскольку элементы выборки считаем независимыми, то многомерный закон распределения равен произведению одномерных: 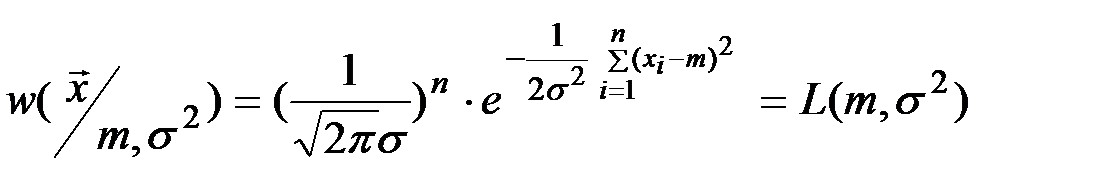 . Это выражение является в то же время функцией правдоподобия
. Это выражение является в то же время функцией правдоподобия 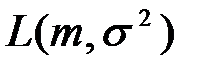 , если ее аргументами считать
, если ее аргументами считать 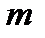 и
и 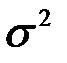 , при постоянном значении выборки
, при постоянном значении выборки 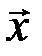 . Функции
. Функции 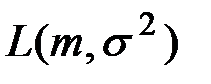 и
и 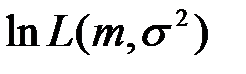 достигают своего максимального значения при одних и тех же значениях аргументов, поскольку логарифм является монотонно возрастающей функцией, поэтому, с целью упрощения вычисления оценок, целесообразнее использовать функцию
достигают своего максимального значения при одних и тех же значениях аргументов, поскольку логарифм является монотонно возрастающей функцией, поэтому, с целью упрощения вычисления оценок, целесообразнее использовать функцию
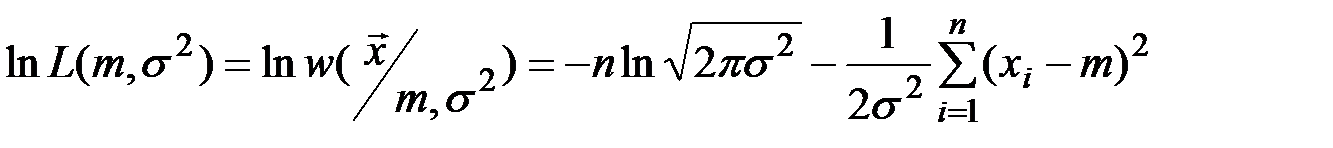 .
.
Чтобы найти максимум, берем производные от ln 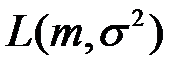 по
по 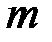 и
и 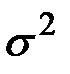 и приравниваем их к нулю:
и приравниваем их к нулю:
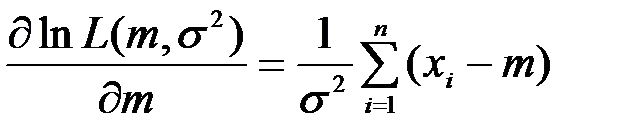 = 0
= 0
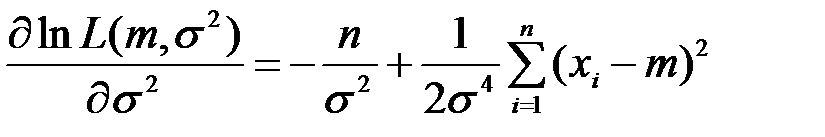 = 0
= 0
После упрощения получим систему уравнений:
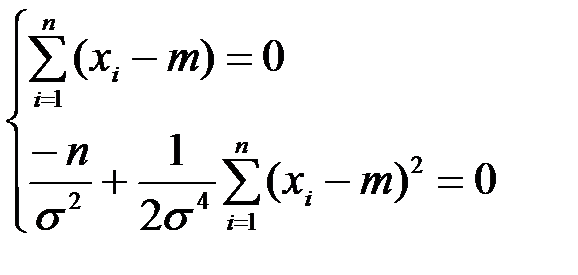
Решая эту систему уравнений, получим
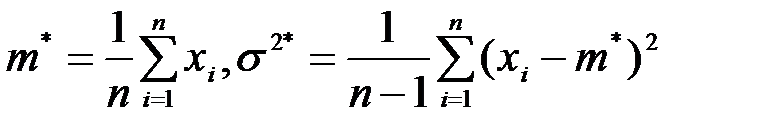 ,
,
где 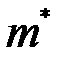 - выборочное среднее,
- выборочное среднее, 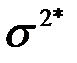 - выборочная дисперсия.
- выборочная дисперсия.
Метод моментов
Все параметры закона распределения можно разделить на две группы: моменты и все остальные. Считаем, что моменты можно оценить экспериментально по выборке 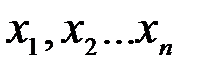 . Такие оценки называются выборочными. Тогда оценку параметра
. Такие оценки называются выборочными. Тогда оценку параметра 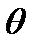 можно получить как функцию выборочного момента, например
можно получить как функцию выборочного момента, например 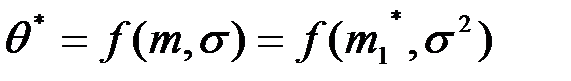 . Для этого достаточно теоретический момент приравнять эмпирическому моменту того же порядка, в результате чего получится уравнение, которое устанавливает связь между параметром
. Для этого достаточно теоретический момент приравнять эмпирическому моменту того же порядка, в результате чего получится уравнение, которое устанавливает связь между параметром 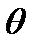 и выборочным моментом. Если неизвестным является один параметр, то достаточно одного уравнения. В противном случае приходится решать систему уравнений, в которых участвуют разные моменты. Выбор моментов осуществляется экспериментально.
и выборочным моментом. Если неизвестным является один параметр, то достаточно одного уравнения. В противном случае приходится решать систему уравнений, в которых участвуют разные моменты. Выбор моментов осуществляется экспериментально.
Пример. Вычислить точечные оценки неизвестных параметров 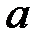 и
и 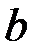 равномерного распределения, плотность которого
равномерного распределения, плотность которого 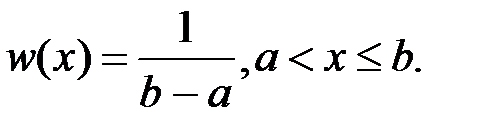
Решение. Поскольку неизвестных параметров два, то необходимо иметь два линейно независимых уравнения. Выражения для выбранных теоретических моментов дисперсии 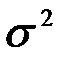 и математического ожидания
и математического ожидания 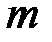 имеют вид
имеют вид 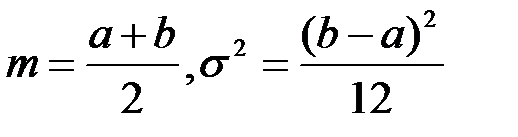 или
или 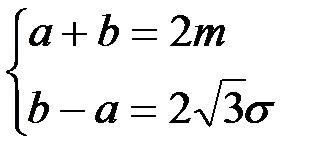 . Решая систему уравнений, получим
. Решая систему уравнений, получим 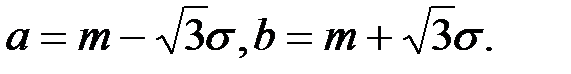 Подставляя вместо
Подставляя вместо  и
и 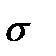 их оценки, получим оценки параметров:
их оценки, получим оценки параметров: 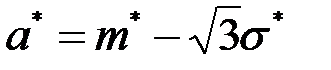 и
и 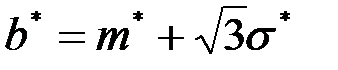 .
.
Выборочные оценки 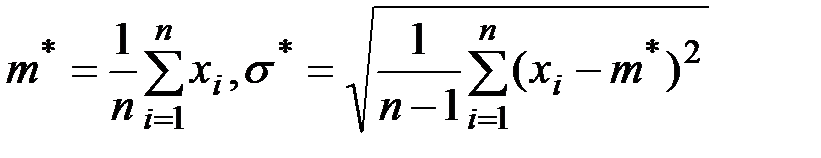 . Следует отметить, что оценки, полученные методом моментов, не всегда являются оптимальными.
. Следует отметить, что оценки, полученные методом моментов, не всегда являются оптимальными.
Выражение для дисперсии 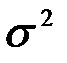 можно получить следующим образом. Если случайную величину умножить на некоторый масштабный коэффициент
можно получить следующим образом. Если случайную величину умножить на некоторый масштабный коэффициент 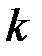 , то дисперсия изменится в
, то дисперсия изменится в 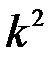 раз. Дисперсия равномерного на отрезке
раз. Дисперсия равномерного на отрезке 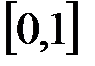 закона распределения равна
закона распределения равна 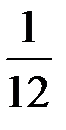 . Поскольку дисперсия
. Поскольку дисперсия 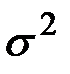 не зависит от математического ожидания, то остается зависимость только от длины интервала
не зависит от математического ожидания, то остается зависимость только от длины интервала 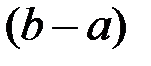 , которая является масштабным коэффициентом по отношению к случайной величине, определенной на единичном отрезке
, которая является масштабным коэффициентом по отношению к случайной величине, определенной на единичном отрезке 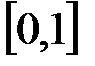 . Поэтому дисперсия
. Поэтому дисперсия 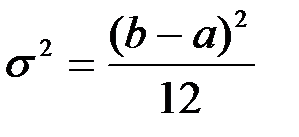 .
.
