Выборка без возвращения и с возвращением
При классическом способе вычисления вероятности, когда все элементарные события равновероятны, широко используется комбинаторика. Мы будем использовать комбинаторные понятия размещения, перестановки и сочетания.
Размещением из 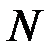 элементов множества
элементов множества 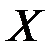 по
по 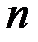 элементам (местам) (коротко, размещением из
элементам (местам) (коротко, размещением из 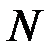 по
по 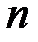 ) назовем любой упорядоченный набор из
) назовем любой упорядоченный набор из 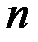 элементов множества
элементов множества 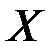 . Два размещения равны тогда и только тогда, когда равны элементы в соответствующих разрядах (позициях).
. Два размещения равны тогда и только тогда, когда равны элементы в соответствующих разрядах (позициях).
Сочетанием из 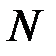 элементов множества
элементов множества 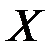 по
по 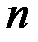 назовем любое подмножество, содержащее
назовем любое подмножество, содержащее 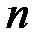 элементов множества
элементов множества 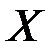 , при этом сочетания различаются только составом.
, при этом сочетания различаются только составом.
Количество размещений 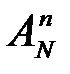 из
из 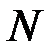 по
по 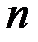 при
при 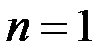 равно
равно 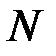 , при
, при 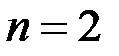 равно
равно 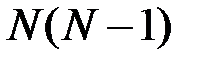 , поскольку на втором месте в последовательности (в размещении) может находиться только один из
, поскольку на втором месте в последовательности (в размещении) может находиться только один из 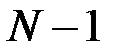 оставшихся элементов. Таким образом, по индукции
оставшихся элементов. Таким образом, по индукции 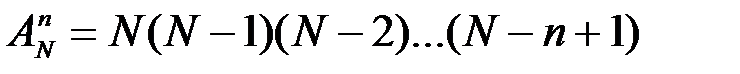 .
.
Количество размещений 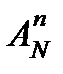 при
при 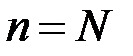 равно
равно 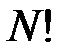 , т.е. равно количеству перестановок, которые можно получить из
, т.е. равно количеству перестановок, которые можно получить из 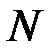 элементов множества
элементов множества 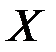 . Таким образом, пространство элементарных событий состоит из
. Таким образом, пространство элементарных событий состоит из 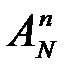 размещений.
размещений.
Количество сочетаний 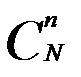 из
из 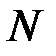 по
по 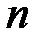 можно вычислить следующим образом. Множество (пространство элементарных событий) всех последовательностей (размещений) с длиной, равной
можно вычислить следующим образом. Множество (пространство элементарных событий) всех последовательностей (размещений) с длиной, равной 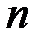 , можно разбить на непересекающиеся подмножества, каждое из которых содержит последовательности, различающиеся только перестановкой элементов и не различающиеся составом (рис. 1.7.).
, можно разбить на непересекающиеся подмножества, каждое из которых содержит последовательности, различающиеся только перестановкой элементов и не различающиеся составом (рис. 1.7.).
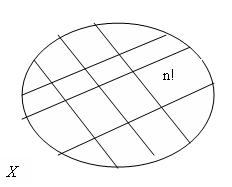 |
| Рис.1.7. Пространство элементарных событий |
Каждое из подмножеств содержит n! последовательностей. Поэтому количество сочетаний 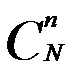 равно количеству подмножеств в пространстве элементарных событий:
равно количеству подмножеств в пространстве элементарных событий: 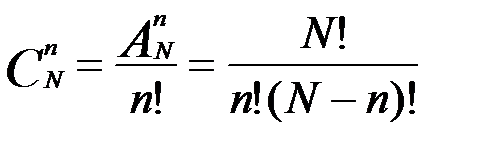
Задача. Всего в урне находится N шаров, среди которых M белых и N-M черных. Какова вероятность того, что среди n вынутых без возвращения шаров, белых окажется ровно 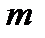 ?
?
Решение:
Все возможные размещения из N шаров по n местам, количество которых равно 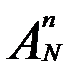 , образуют пространство элементарных событий. Вычислим количество благоприятствующих событий, т.е. количество последовательностей (размещений), каждая из которых содержит
, образуют пространство элементарных событий. Вычислим количество благоприятствующих событий, т.е. количество последовательностей (размещений), каждая из которых содержит 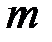 белых шаров.
белых шаров.
1. Если все белые шары в последовательности считать неразличимыми, то количество способов, которыми можно получить все различающиеся между собой последовательности, равно количеству способов 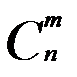 , которыми можно выбрать m мест (подмножеств) для размещения белых шаров в последовательности с длиной, равной n. При этом состав шаров в последовательности не меняется, а меняется только состав выбранных мест для размещения белых шаров.
, которыми можно выбрать m мест (подмножеств) для размещения белых шаров в последовательности с длиной, равной n. При этом состав шаров в последовательности не меняется, а меняется только состав выбранных мест для размещения белых шаров.
2. Если все белые шары в урне считать различными, то последовательности могут различаться в m выбранных для белых шаров местах 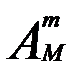 способами.
способами.
3. Следовательно, если все черные шары в урне считать различными, то последовательности могут различаться в n-m местах 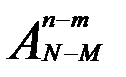 способами. Тогда общее количество благоприятствующих последовательностей будет равно
способами. Тогда общее количество благоприятствующих последовательностей будет равно 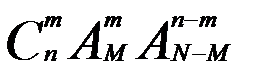 , а вероятность появления m белых шаров среди n вынутых будет равна
, а вероятность появления m белых шаров среди n вынутых будет равна 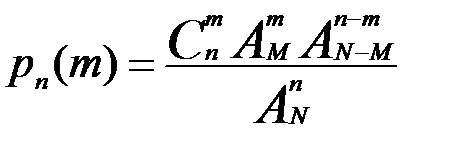 , где
, где 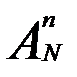 - количество элементарных событий в вероятностном пространстве. Если в последнем равенстве сделать подстановку
- количество элементарных событий в вероятностном пространстве. Если в последнем равенстве сделать подстановку 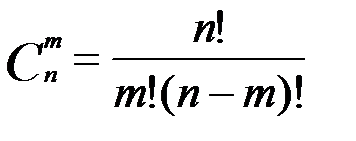 и учесть, что
и учесть, что 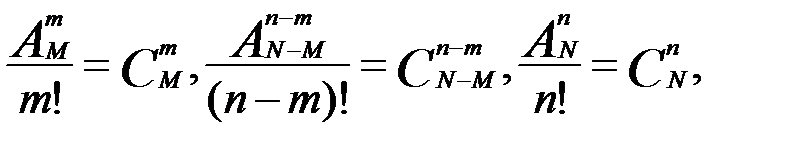 то получим
то получим 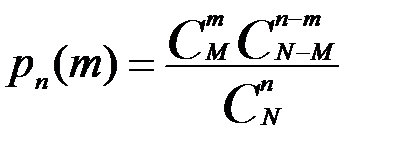 .
.
Эту задачу можно решить, используя вероятностное пространство более высокого иерархического уровня, когда все последовательности с одинаковым составом рассматриваются как одно событие, т.е. образуют некоторое подмножество в пространстве элементарных событий.
Результат опыта состоит из m белых шаров и n-m – черных. Результаты опыта различаются составом белых шаров и составом черных шаров. Состав – это подмножество из m белых шаров, выбранных из M белых шаров, находящихся в урне, и аналогично подмножество из n-m черных шаров, выбранных из N-M черных шаров, находящихся в урне. Количество таких подмножеств соответственно равно  и
и 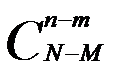 .
.
Общее количество возможных результатов опыта определяется как произведение 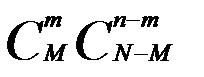 .
.
В данном случае все указанные результаты опыта образуют подмножество благоприятствующих событий в пространстве элементарных событий, а все пространство содержит 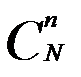 исходов. Отсюда искомая вероятность будет равна
исходов. Отсюда искомая вероятность будет равна 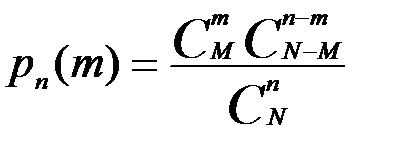
Это решение демонстрирует, как можно решать задачи с использованием вероятностных пространств на разных иерархических уровнях, но при этом нужно иметь в виду, что, продвигаясь вверх по иерархическим уровням, можно потерять часть информации, необходимой для решения конкретной задачи.
Задача. Вычислить вероятность того, что из урны, содержащей 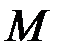 белых шаров и
белых шаров и 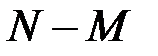 черных, будет вынута заданная последовательность шаров. Например, белый, черный, белый (n=3).
черных, будет вынута заданная последовательность шаров. Например, белый, черный, белый (n=3).
Решение. В общем случае последовательность вынутых шаров можно записать как последовательность событий 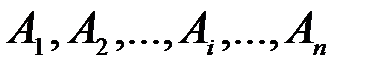 , где
, где
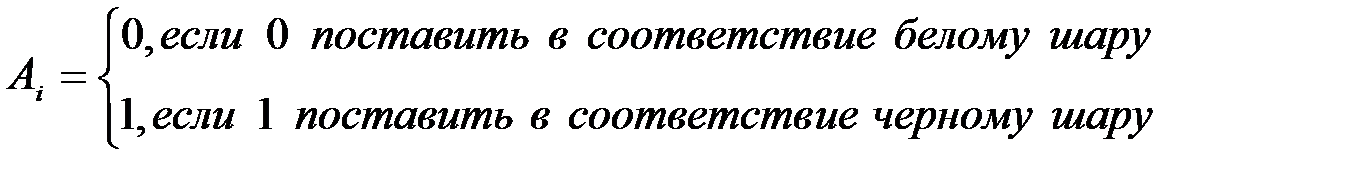
Вероятность 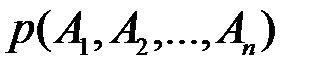 произведения (последовательности) в общем случае зависимых событий
произведения (последовательности) в общем случае зависимых событий 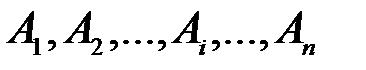 равна
равна 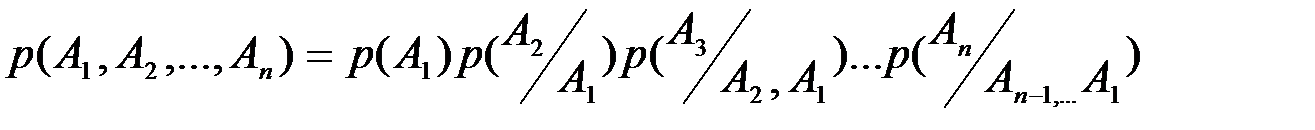 , причем результат произведения событий и вероятность
, причем результат произведения событий и вероятность 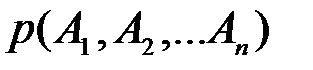 не зависят от порядка сомножителей
не зависят от порядка сомножителей 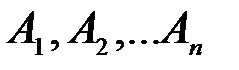 , выбор которого иногда позволяет значительно упростить процедуру вычислений. Такая запись позволяет интерпретировать произведение событий как их последовательную реализацию, причем вероятность очередного события зависит от всех предыдущих реализованных событий. Все события, которые были реализованы перед очередным событием, изменяют комплекс условий, при котором появляется очередное событие, и тем самым влияют на вероятность его появления. В данном случае результат опыта можно записать в виде последовательности 010
, выбор которого иногда позволяет значительно упростить процедуру вычислений. Такая запись позволяет интерпретировать произведение событий как их последовательную реализацию, причем вероятность очередного события зависит от всех предыдущих реализованных событий. Все события, которые были реализованы перед очередным событием, изменяют комплекс условий, при котором появляется очередное событие, и тем самым влияют на вероятность его появления. В данном случае результат опыта можно записать в виде последовательности 010 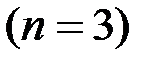 , вероятность которой можно вычислить как вероятность произведения событий:
, вероятность которой можно вычислить как вероятность произведения событий:
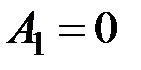 ,
, 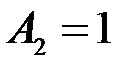 ,
, 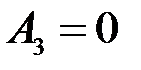 , т.е.
, т.е. 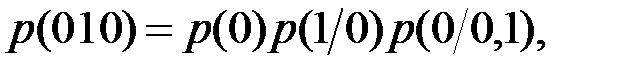 где
где 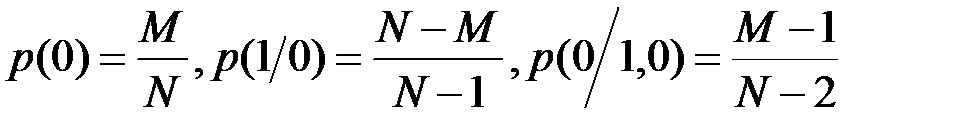 .
.
Отсюда 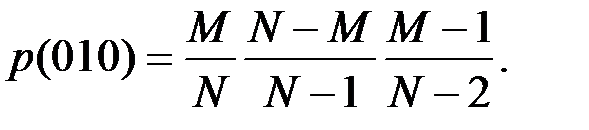
Дадим интерпретацию решения этой задачи в пространстве элементарных событий. Поскольку все шары в урне мы считаем различными, то в пространстве элементарных событий последовательности 010 будет соответствовать подмножество последовательностей, которые различаются составом и порядком как белых, так и черных шаров в отдельности.
Белые шары будут различаться 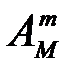 способами, а черные -
способами, а черные - 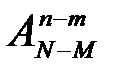 способами. Общее количество последовательностей, которые являются благоприятствующими для события 010, будет равно
способами. Общее количество последовательностей, которые являются благоприятствующими для события 010, будет равно 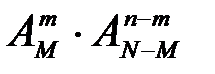 , а вероятность появления заданной последовательности будет равна
, а вероятность появления заданной последовательности будет равна 
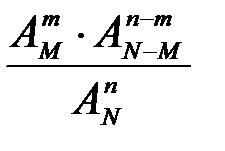 .
.
При 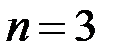 и
и 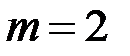 получим
получим 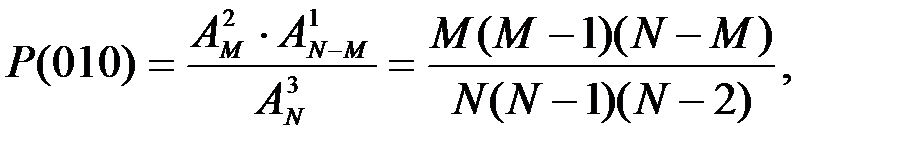 что совпадает с выше полученным результатом. Следует отметить, что вероятность не зависит от порядка расположения нулей и единиц в заданной последовательности.
что совпадает с выше полученным результатом. Следует отметить, что вероятность не зависит от порядка расположения нулей и единиц в заданной последовательности.
1.6. Нелинейное преобразование случайных величин
Пусть характеристика нелинейного элемента (НЭ) вход/выход задана зависимостью 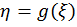 имеющей однозначную обратную зависимость
имеющей однозначную обратную зависимость 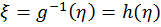 .
.
Вероятность того, что реализация х случайной величины 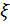 попадает в интервал
попадает в интервал 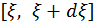 равна вероятности того, что реализация случайной величины
равна вероятности того, что реализация случайной величины 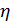 попадает в интервал
попадает в интервал 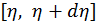 , т.е. при преобразовании сохраняется вероятностная мера событий:
, т.е. при преобразовании сохраняется вероятностная мера событий:
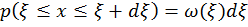
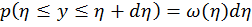
и 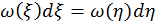
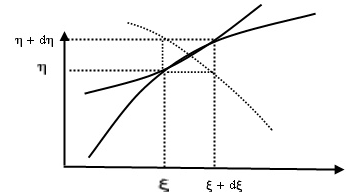
Рис. 1.8. Нелинейное преобразование 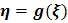
Отсюда 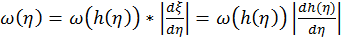 .
.
В последнем используется значение модуля производной, поскольку результат не зависит от того, каким образом одна область отображается в другую.
Аналогично решается задача преобразования многомерных плотностей. Пусть известна n-мерная плотность 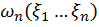 случайных величин
случайных величин 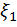 ,
, 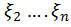 и нужно найти плотность
и нужно найти плотность 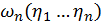 для случайных величин
для случайных величин
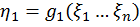
…………………………
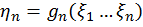 ,
,
где функции (нелинейные преобразования) 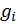 – кусочно-непрерывные функции. Предполагается, что существуют однозначные обратные функции
– кусочно-непрерывные функции. Предполагается, что существуют однозначные обратные функции
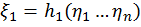
………………………….
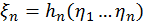
При попадании вектора 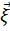 в область
в область 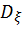
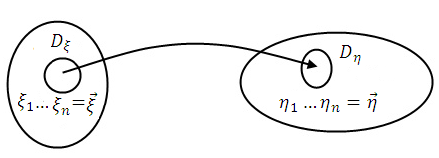
Рис. 1.9. Геометричесая интерпретация нелинейного преобразования
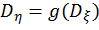 . При этом справедливо равенство
. При этом справедливо равенство 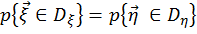 , если
, если
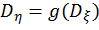 . Если выбрать в качестве
. Если выбрать в качестве 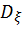 элементарные объемы
элементарные объемы 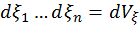 , а в качестве
, а в качестве 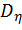 элементарный объем
элементарный объем 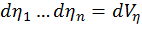 , то
, то
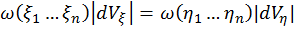 и
и
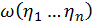 =
= 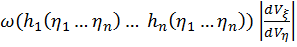
Отношение элементарных объемов при преобразовании координат
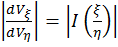 , где
, где 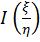 - якобиан преобразования от случайных величин
- якобиан преобразования от случайных величин 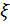 к случайным величинам
к случайным величинам 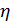 , модуль которого равен:
, модуль которого равен:
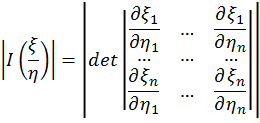
В общем случае значение якобиана может зависеть от координат 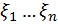 . Если зависимость отсутствует, то преобразование называется линейным.
. Если зависимость отсутствует, то преобразование называется линейным.
Закон распределения Релея
Пусть имеется вектор 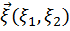 . Координаты
. Координаты 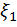 и
и 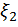 – независимые центрированные случайные величины с одинаковым гауссовым законом распределения. Тогда двумерное распределение
– независимые центрированные случайные величины с одинаковым гауссовым законом распределения. Тогда двумерное распределение
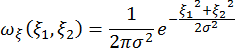
Определим плотность распределения амплитуды а и фазы φ вектора с координатами 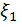 и
и 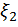 .
.
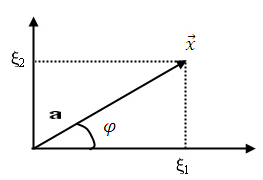
Рис. 1.10. Геометрическая интерпретация нелинейного преобразования
1 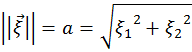
1 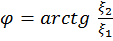 =
= 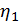
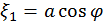
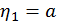
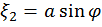
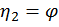
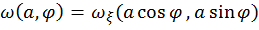 |det
|det 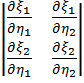 | =
| =
= 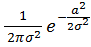 |det
|det 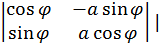 ;
;
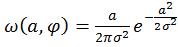 ,
,
0 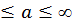 ,
, 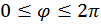 .
.
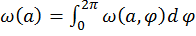 =
= 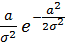 - закон распределения Релея.
- закон распределения Релея.
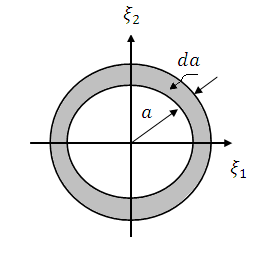
Рис. 1.11. Геометрическая интерпретация закона Релея
Вероятность 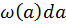 равна вероятности того, что конец вектора
равна вероятности того, что конец вектора 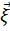 попадет в кольцо с шириной, равной
попадет в кольцо с шириной, равной 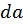 и радиусом, равным
и радиусом, равным 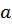 (рис. 1.11).
(рис. 1.11).
Аналогично находится плотность распределения вероятностей фазы:
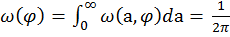 . Поскольку
. Поскольку 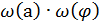 , то
, то 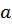 и
и 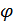 независимые случайные величины.
независимые случайные величины.
Вероятность 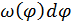 равна вероятности того, что конец вектора
равна вероятности того, что конец вектора 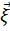 попадет в конус с углом, равным
попадет в конус с углом, равным 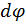 .
.
Этот результат широко используется при анализе узкополосного нормального шума.
Рассмотрим ещё один пример нелинейного преобразования. Пусть случайная величина 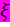 имеет закон распределения Релея
имеет закон распределения Релея
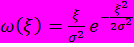 при
при  и нулю при
и нулю при 
Нелинейное преобразование задается функцией 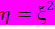 .
.
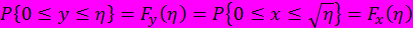 , где у и х – реализации случайных величин
, где у и х – реализации случайных величин 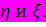
Здесь область  определяется неравенством 0<ξ<
определяется неравенством 0<ξ< 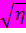 а область
а область 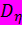 - интервалом (0,
- интервалом (0, 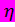 ) (рис. 1.12).
) (рис. 1.12).
Из равенства  =
=  следует:
следует:
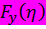 =
= 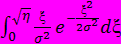 =
= 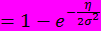 ,
, 
И
1 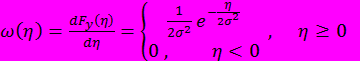
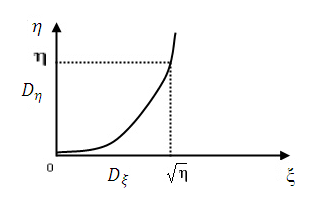
Рис. 1.12. Нелинейное преобразование 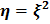
1.6.2. Геометрическая интерпретация нелинейного преобразования случайной величины.
На практике функцию g(x), которая описывает нелинейное преобразование, удобно аппроксимировать линейно-ломаной функцией, которая представляет собой последовательность отрезков разной длины, при этом точность аппроксимации повышается с уменьшением длин отрезков (рис. 1.13).
Таким образом, нелинейное преобразование можно аппроксимировать последовательностью линейных преобразований, каждое из которых отображает некоторую область на оси х в соответствую область на оси у, например, интервал [a b] – в интервал [d c] (рис. 1.13).
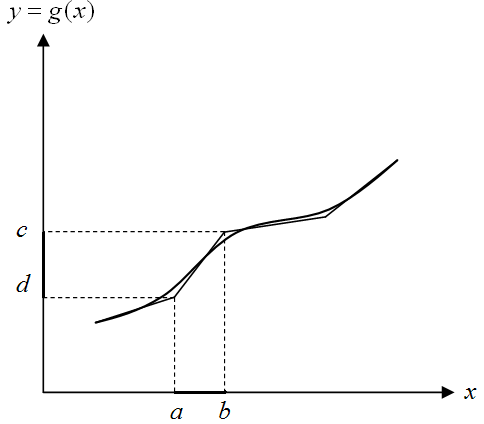
Рис. 1.13. Аппроксимация нелинейной функции g(x) линейно-ломаной функцией
Некоторые особенности линейного преобразования проявляются в зависимости от расположения отрезка: горизонтального, вертикального и под некоторым углом. Эти особенности рассмотрим на конкретных примерах.
| в) |
| б) |
| а) |
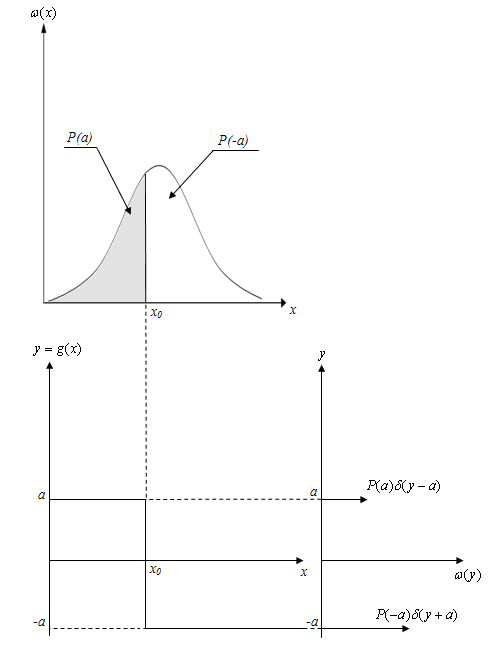
Рис. 1.14. Геометрическое представление нелинейного преобразования случайной величины
а) Исходный закон распределения; б) нелинейное преобразование в виде z-функции; в) закон распределения случайной величины у, полученной в результате нелинейного преобразования
На рис. 1.14 продемонстрирован процесс нелинейного преобразования непрерывной случайной величины х в дискретную случайную величину 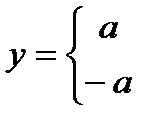 .
.
В этом случае вероятность p(-a) = p(x0<x), а вероятность p(a) = p(x<x0), при этом вероятность p(x0<x) равна площади под плотностью распределения 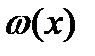 правее x0, а вероятность p(x<x0) – левее x0.
правее x0, а вероятность p(x<x0) – левее x0.
Закон распределения дискретной случайной величины можно описать в виде плотности распределения вероятностей, если воспользоваться дельта-функцией: 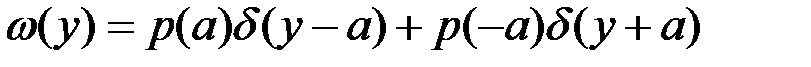 , где дельта функция
, где дельта функция
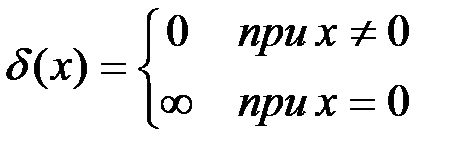 и
и 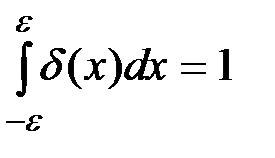 .
.
Геометрически δ-функция изображается стрелкой.
Дельта-функцию можно рассматривать как предел последовательности функций, площадь под которыми всегда равна единице, а значение в точке x=0 неограниченно растет. В частном случае δ-функцию можно получить как предел функции, изображенной на рис. , где значение ε является ее параметром.
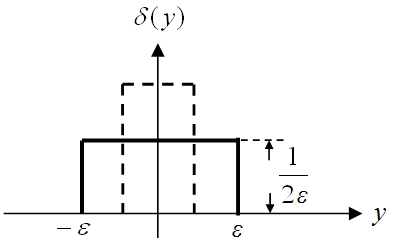
Рис. 1.15. δ-функция ______
При стремлении значения ε к нулю в пределе получается δ-функция.
Таким образом, наличие горизонтальных участков в линейно-ломаной функции всегда приводит к появлению δ-функций в плотности распределения 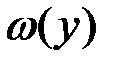 преобразованной случайной величины.
преобразованной случайной величины.
Рассмотрим преобразование случайной величины, линейно-ломаная функция которого содержит отрезок, расположенный под некоторым углом (рис. 1.16)
| в) |
| б) |
| а) |
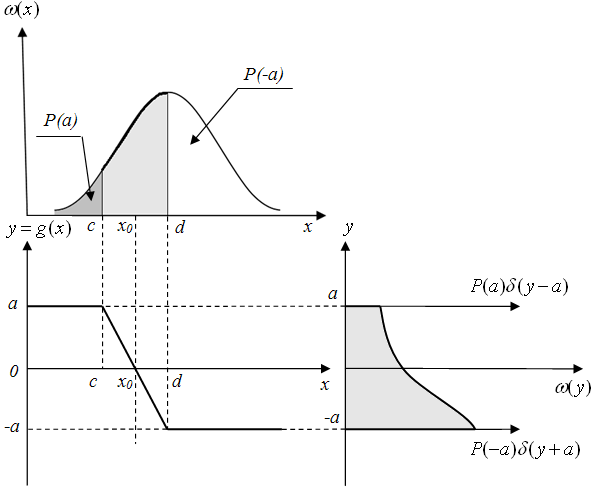
Рис. 1.16. Геометрическое представление нелинейного преобразования случайной величины
а) Исходный закон распределения; б) нелинейное преобразование; в) закон распределения случайной величины у, полученной в результате нелинейного преобразования)
В этом случае вероятность 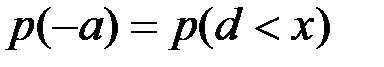 , а вероятность
, а вероятность 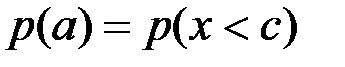 . Случайная величина х на интервале [c,d] преобразуется линейно с масштабным коэффициентом k, равным
. Случайная величина х на интервале [c,d] преобразуется линейно с масштабным коэффициентом k, равным 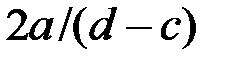 , при этом вероятностная мера интервала [c,d] сохраняется, то есть площадь под плотностью
, при этом вероятностная мера интервала [c,d] сохраняется, то есть площадь под плотностью 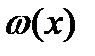 на интервале [c,d]равна площади под плотностью
на интервале [c,d]равна площади под плотностью 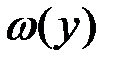 на интервале [-a,a]. Если масштабный коэффициент равен единице
на интервале [-a,a]. Если масштабный коэффициент равен единице 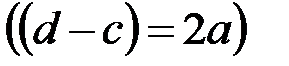 , то плотности
, то плотности 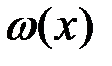 и
и 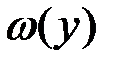 на этих интервалах совпадают при положительном значении тангенса угла наклона отрезка, а при отрицательном – совпадают плотности
на этих интервалах совпадают при положительном значении тангенса угла наклона отрезка, а при отрицательном – совпадают плотности 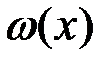 и
и 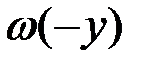 .
.
Таким образом, если длина интервала, равная 2а, увеличивается в k раз по сравнению с интервалом, равным (d-c), то во столько же раз уменьшается масштабный коэффициент по оси 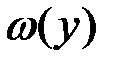 , что обеспечивает сохранение вероятностной меры.
, что обеспечивает сохранение вероятностной меры.
Рассмотрим случай, когда линейно-ломаная функция содержит отрезок с вертикальным расположением (рис. 1.17)
| а) |
| б) |
| в) |
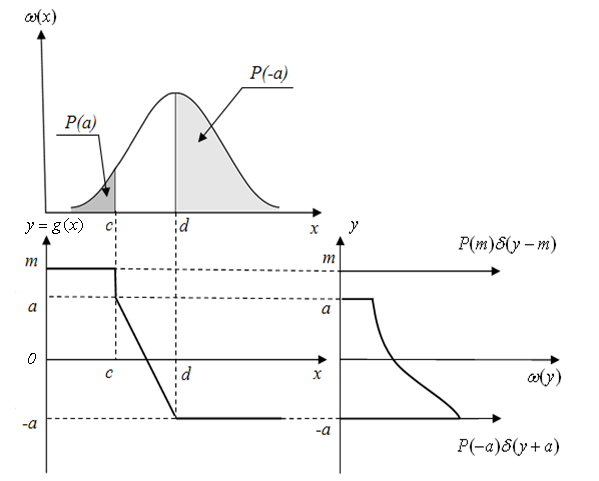
Рис. 1.17. Геометрическое представление нелинейного преобразования случайной величины (линейно-ломаная функция содержит отрезок с вертикальным расположением)
а) Исходный закон распределения, б) нелинейное преобразование; в) закон распределения случайной величины у; полученной в результате нелинейного преобразования)
Этот пример отличается от предыдущего только переносом δ-функции из точки a в точку m, при этом вероятностная мера отрезка (a, m) равна 0, поскольку он является отображением всего одной точки с вероятностной мерой, равной нулю.
В предыдущих примерах линейные преобразования считались взаимно- однозначными. Рассмотрим пример с взаимно-неоднозначным преобразованием (рис. 1.18).
| в) |
| б) |
| а) |
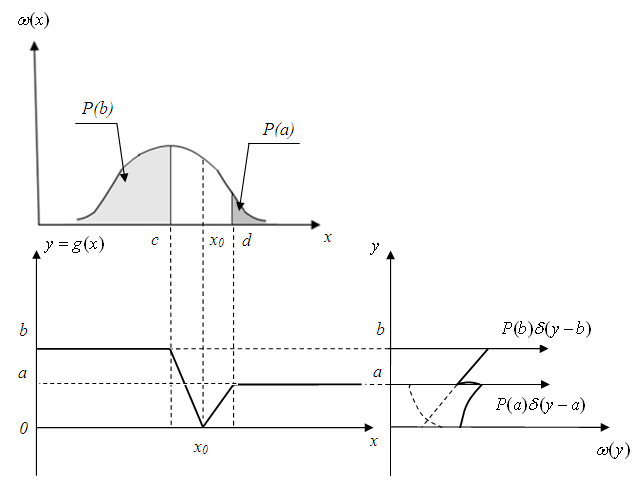
Рис. 1.18. Пример нелинейного взаимно-неоднозначного преобразования случайной величины
а) Исходный закон распределения, б) нелинейное взаимно-неоднозначное преобразование, в) закон распределения случайной величины у, полученной в результате нелинейного взаимно-неоднозначного преобразования)
В этом случае нелинейное преобразование необходимо представить в виде двух взаимно-однозначных преобразований, правее точки x0 и левее, и для каждого из них в отдельности получить результат преобразования. Окончательный результат получается как сумма отдельных результатов, поскольку события правее x0 и левее x0 несовместны. Окончательный результат изображен сплошной линией.
Функция регрессии.
