Вычисление условной вероятности

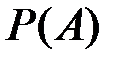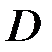Вероятность события при заданном комплексе условий называется полной или безусловной вероятностью и может изменяться только при изменении комплекса условий. Если некоторое событие 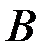так или иначе влияет на комплекс условий, накладывает на него ограничения, то вводится понятие условной вероятности 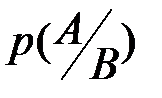события 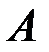при условии .

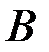При вычислении условной вероятности следует обратить особое внимание на построение пространства элементарных событий. Оно должно содержать в себе события 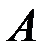и как некоторые подмножества (Рис 1.1). В этом случае условная вероятность

определяется на подмножестве 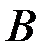как новом пространстве элементарных событий, в котором событие существует в виде пересечения 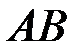событи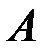й и 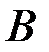, при этом элементарные события в 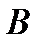образуют полную группу событий благодаря делению значений их вероятностей на . Условную вероятность 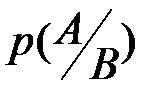можно интерпретировать как вес события по отношению к весу события 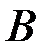. В частности, событие 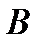может совпасть со всем пространством 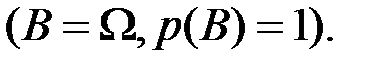В этом случае вероятность события 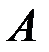может зависеть от события , так как реализация события 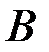может привести к изменению закона распределения вероятностей элементарных событий и благоприятствующих для 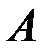в том числе.

Пример. Пусть произошло событие 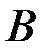, состоящее в том, что из двух возможных кубиков со смещенным центром массы и несмещенным, случайным образом выбран кубик со смещенным центром массы. В этом случае событие 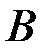совпадает со всем пространством, а вероятность события 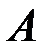в 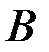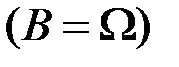будет определяться законом распределения вероятностей появления цифр при выбранном кубике. В принципе, все события являются условными, так как появляются при том или ином комплексе условий.

Если все события в подмножестве равновероятны, то применим классический метод вычисления вероятностей, который сводится к вычислению отношения количества элементарных событий в 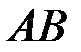(благоприятствующих для события 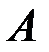в подмножестве 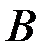) к количеству элементарных событий в подмножестве .

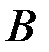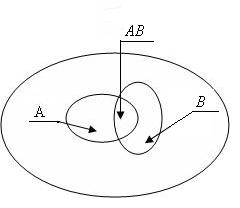Рис 1.1. Пространство элементарных событий

Например, если по условию задачи кубик бросают два раза, то исходом опыта будут две цифры, которые можно рассматривать как координаты точки на плоскости. В этом случае пространство состоит из 36 точек, а не из 6 как иногда ошибочно считают.

В данном случае опыт состоит из двух испытаний (бросаний кубика) и пространство элементарных событий (исходов опыта) представляет собой декартово произведение пространств отдельных испытаний.

Опыт может содержать произвольное количество испытаний. Этой терминологии мы будем придерживаться и в дальнейшем.

Задача. Студент выучил 10 билетов из 25. В каком случае вероятность вынуть выученный билет больше, когда студент вынимает билет первым или вторым (билеты не возвращаются)?

Решение. Результатом опыта являются два вынутых билета, т. е. их номера. Не нарушая общности решения, выученными билетами будем считать первые 10.

Исходы первого испытания будем откладывать по оси 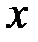, а второго - по оси 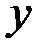(рис. 1.2).

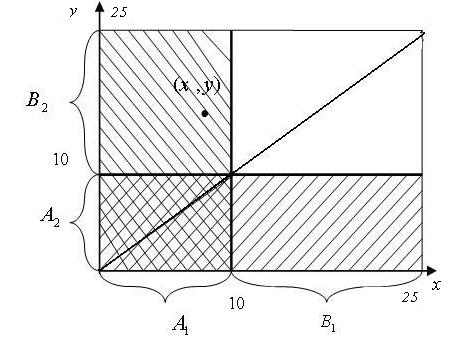Рис 1.2. Пространство элементарных событий

Точка с координатами 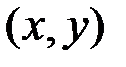соответствует исходу опыта. Поскольку билеты не возвращаются, то события, которым соответствуют точки, лежащие на диагонали, являются невозможными и их следует исключить из пространства элементарных событий. Все остальные события, количество которых равно 25*25-25=25*24, можно считать равновероятными, и поэтому применим классический метод вычисления вероятности. Тогда вероятность события 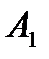, состоящего в том, что при первом испытании будет вынут выученный билет, равна .

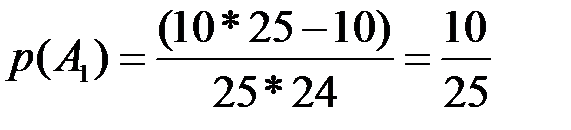Аналогично вероятность события 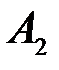, состоящего в том, что второй вынутый билет окажется выученным, равна .

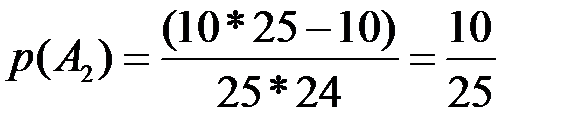Следовательно, .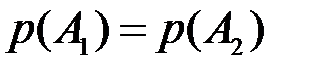

Кроме событи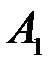й и 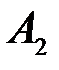, в данном пространстве элементарных событий можно выделить много других событий и вычислить их вероятности. Например, вероятности событий 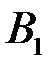(первый вынутый билет оказался не выученным) и 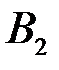(второй вынутый билет оказался невыученным) равны , .

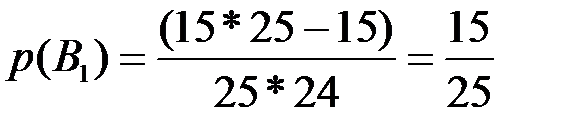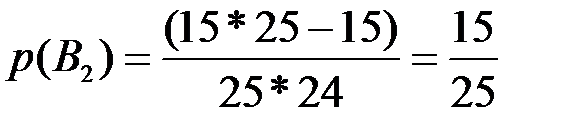Вероятность произведения событий 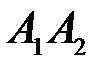равна .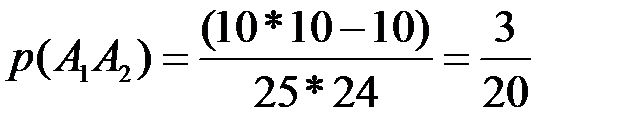

Условные вероятности:

и 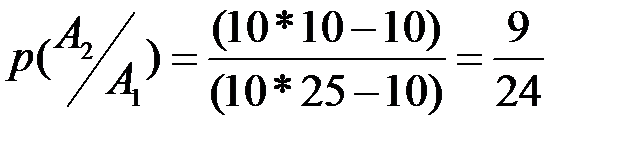, где в числителе стоит количество элементарных событий, которые входят в пересечение событи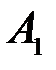й и 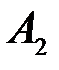, а в знаменателе- количество элементарных событий, которые входят соответственно в 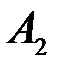и 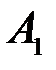. Поясним физический смысл условных вероятностей: 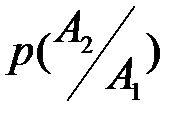- это вероятность того, что при втором испытании появится выученный билет при условии, что первым был также выученный билет. Событие 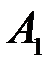изменило комплекс условий, при котором совершается второе испытание; 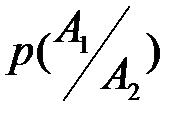-это вероятность того, что билет, вынутый первым, был выученным при условии, что второй билет оказался выученным, при этом предполагается, что мы не смотрели, каким был билет, вынутый первым. Вычислите условные вероятности для других событий.

Задача. Кубик бросают два раза. С какой вероятностью при первом испытании появится единица (событие 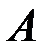) при условии, что при втором испытании на кубике выпало значение больше, чем при первом (событие ).

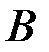Решение. Применим классический метод вычисления вероятностей, поскольку исходы опыта образуют пространство равновероятных элементарных событий (Рис. 1.3).

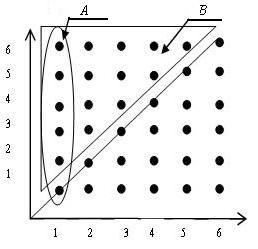Рис. 1.3. Пространство элементарных событий

Необходимо вычислить условную вероятность

,

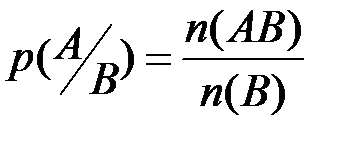где 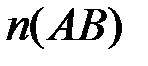- количество точек, входящих в пересечение событи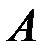й и 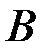, равное 5; 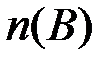- количество точек, входящих в подмножество 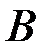, равное 15. Подмножество 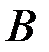образовано точками, лежащими строго выше диагонали. Следовательно, .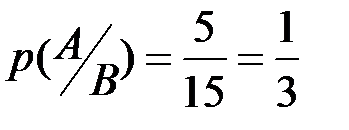