Д.В. Ломакин, Л.С. Ломакина, А.С. Пожидаева

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

«НИЖЕГОРОДСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

Им. Р.Е. АЛЕКСЕЕВА»

Д.В. Ломакин, Л.С. Ломакина, А.С. Пожидаева

ВЕРОЯТНОСТЬ. ИНФОРМАЦИЯ. КЛАССИФИКАЦИЯ.

Рекомендовано Ученым советом Нижегородского государственного технического университета им. Р. Е. Алексеева в качестве учебного пособия для студентов высших учебных заведений, обучающихся по направлению подготовки 230100 «Информатика и вычислительная техника» и 230400 «Информационные системы и технологии»

Нижний Новгород

УДК 005

Рецензент:

Доцент кафедры теоретической механики

Нижегородского государственного университета

им. Н.И. Лобачевского, кандидат физико-математических наук,

доцент А.Ф. Ляхов

Д.В. Ломакин, Л.С. Ломакина, А.С. Пожидаева

Вероятность. Информация. Классификация:учеб. пособие /

Д.В. Ломакин, Л.С. Ломакина, А.С. Пожидаева

Нижегор. гос. техн. ун–т им. Р.Е. Алексеева. – Н. Новгород, 2014. – 128с.

Рассматриваются базовые понятия теории вероятностей, теории информации и использование вероятностных и информационных методов в задачах диагностики сложных систем и в задачах обработки многомерных данных на примере классификации состояний биоценоза.

Учебное пособие предназначено для студентов, обучающихся по направлениям: 230100 «Информатика и вычислительная техника» и 230400 «Информационные системы и технологии»

Рис. 42. Табл. 6. Библиогр.: 10 назв.

УДК 005

	© Нижегородский государственный технический университет им. Р.Е. Алексеева, 2013 © Д.В. Ломакин, Л.С. Ломакина, А.С. Пожидаева 2013

ВВЕДЕНИЕ

В настоящее время широко используется системный подход к решению задач анализа и синтеза объектов и процессов различной физической природы. Объект описывается как система, т. е., как структурированный состав, при этом свойства объекта определяются свойствами построенной системы, которая выполняет функцию модели объекта при решении поставленной задачи. Исследование свойств модели, моделирование свойств с использованием современных информационных технологий, и синтез на основе результатов моделирования новых объектов, процессов и концепций является основной частью научной и прикладной деятельности человека.

Описать состояние объекта как некоторой целостности минимальным количеством переменных (параметров, свойств) на ранних стадиях его изучения, как правило, не представляется возможным, не всегда удается даже определить их возможное количество. Поэтому на первом этапе возникает проблема с выделением наиболее информативной совокупности переменных, на основании которой можно было бы решить поставленную задачу, которая описывается заданной целевой функцией.

Кроме наблюдаемых переменных существуют еще скрытые переменные (компоненты), которые отражают структурные свойства объекта, законы, определяющие форму организации объекта. Совокупность значений наблюдаемых переменных называется многомерными данными в пространстве переменных.

К настоящему времени сформировалось несколько методов обработки многомерных данных, каждый из которых решает частную задачу. В настоящем пособии приведен обзор методов и подробно рассматривается метод классификации на примере анализа состояний биоценоза.

Для решения задач, связанных с обработкой многомерных данных, требуется соответствующий инструментарий, функции которого могут выполнять методы теории вероятностей, теории информации и математической статистики. Поэтому в пособии подробно описан их понятийный аппарат и способы решения конкретных задач.

ВЕРОЯТНОСТЬ

Основные понятия

Каждая наука начинается с определения объекта и предмета исследования, построения модели объекта, системы аксиом и с формирования основных понятий, на которых она базируется [1,3,4,5,7]. Поскольку определить понятие – это значит свести его к другим, более известным понятиям, то, очевидно, процесс должен где-то закончиться. Поэтому всегда существуют первичные понятия, которые строго не определяются, а только поясняются. Одним из таких понятий является понятие события.

В теории вероятностей объект исследования - это случайные явления различной физической природы.

Предметом теории вероятностей является математический анализ случайных явлений, выявление закономерностей в самих случайных явлениях независимо от их конкретной природы.

Событие – это любой факт, который может произойти при заданном комплексе условий .

Достоверное событие – это событие, которое всегда происходит при заданном комплексе условий .

Невозможное событие - это событие, которое никогда не происходит при заданном комплексе условий .

Случайное событие – это событие, которое может произойти, а может и не произойти при заданном комплексе условий .

Следует отметить, что достоверное, невозможное и случайное события остаются таковыми только при заданном комплексе условий .

Комплекс условий – это совокупность контролируемых физических величин или параметров, которые описывают эксперимент, испытание, опыт и т.д. Задать комплекс условий – это значит задать значения указанных физических величин или параметров.

Эмпирическим основанием для построения теории вероятностей послужила устойчивость относительной частоты появления события. Если при n испытаниях событие появилось раз, то его относительная частота появления равна отношению . Это свойство относительной частоты выражено в (одной из основных) аксиоме Колмогорова, согласно которой

Вероятность – это число , которое поставлено в соответствие данному событию. Значение вероятности иногда называют вероятностной мерой или весом события. Вероятность можно интерпретировать как степень возможности появления события.

Модель, лежащая в основе теории вероятностей, - это пространство элементарных событий, которое по определению представляет собой полную группу несовместных событий (исходов данного опыта, эксперимента) с заданной вероятностной мерой (законом распределения вероятностей).

События называются несовместными, если наступление одного из них исключает возможность наступления другого.

События образуют полную группу событий, если , где – вероятность і– го события, т.е. вероятность появления события, которое не принадлежит данной группе, равна нулю.

Математическая модель события (в отличие от приведенного выше пояснения физического смысла события) – это любое подмножество в пространстве элементарных событий, чаще всего объединенных в подмножество по тому или иному свойству, признаку.

В теории вероятностей не исследуются причины, по которым события появляются с той или иной вероятностью. Основной ее задачей является разработка методов вычисления вероятностей, если известны вероятности элементарных событий или вероятности некоторых исходных событий.

Можно выделить четыре этапа вычисления вероятности события:

· построение пространства элементарных событий, которое определяется комплексом условий в данной задаче;

· выделение подмножества, т.е. события, вероятность которого необходимо вычислить по условию задачи, и событий, которые участвуют в решении задачи;

· вычисление вероятностей элементарных событий, которые входят в выделенное подмножество;

· вычисление вероятности выделенного события как суммы вероятностей всех образующих его элементарных событий.

Указанные этапы желательно представлять при решении любой задачи, но это не значит, что нужно скрупулезно следовать им.

Разработанные в теории вероятностей методы (теоремы) позволяют найти более короткие способы вычисления вероятностей по сравнению с указанным общим методом

В принципе, все вероятности событий являются условными, поскольку все события происходят при том или ином комплексе условий. Тем не менее, любой комплекс условий, который реализуется в данном эксперименте, можно считать полным начальным, т.е. без каких-либо ограничений, а соответствующие вероятности событий - полными или безусловными.

Часто полный комплекс условий можно представить как совокупность частных комплексов условий, которые образуют некоторую вероятностную структуру. Тогда вероятность некоторого события 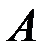при частном комплексе условий можно назвать частной или условной вероятностью.

Рассмотрим следующий способ вероятностной организации совокупности комплексов условий. Пусть имеется 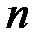комплексов условий, каждый из которых реализуется в данном эксперименте с некоторой вероятностью 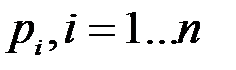. Реализацию некоторого частного комплекса условий будем интерпретировать как появление события 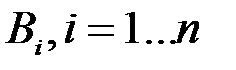с вероятностью, равной 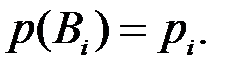Все события 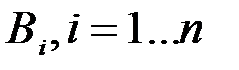образуют полную группу несовместных событий. Требуется вычислить полную вероятность события 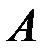, которое может наступить лишь при появлении одного из событий 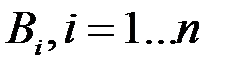с известной условной вероятностью 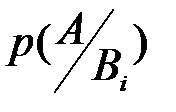и при известных вероятностях 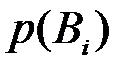. Для событи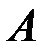й и 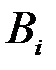можно записать формулу умножения вероятностей в виде

.

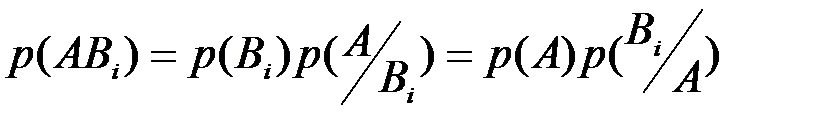Тогда полная вероятность

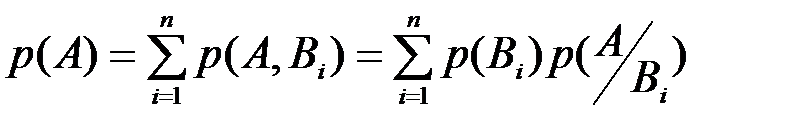
получается в результате суммирования двухмерного закона распределения 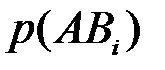по всем событиям 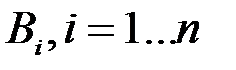, которые требуется исключить, т.е. понизить размерность распределения. Полученное выражение для вычисления вероятности 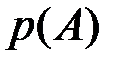называется формулой полной вероятности, геометрическая интерпретация которой представлена в виде вероятностной диаграммы (Рис. 1.4). Вероятность 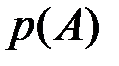равна сумме произведений вероятностей 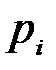на условные вероятности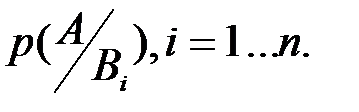

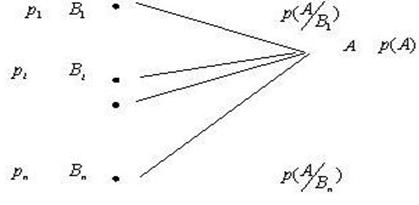
Рис.1.4. Вероятностная диаграмма

Из формулы умножения вероятностей следует, что

.

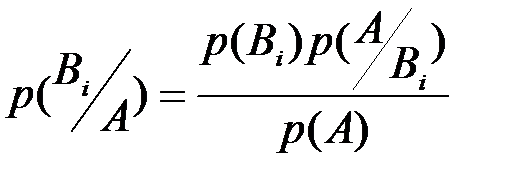Полученное выражение называется формулой Байеса, где 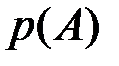вычисляется по формуле полной вероятности.

Формула Байеса позволяет вычислить вероятность события 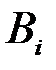при условии, что появилось событие 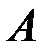. В этом случае события 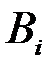называются гипотезами и, как правило, обозначаются через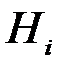 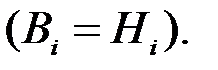Можно дать следующую интерпретацию формулы Байеса. В результате опыта реализуется ненаблюдаемое событие 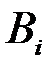с априорной (доопытной) вероятностью, равной 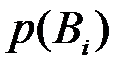, и наблюдаемое событие 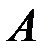, которое доставляет некоторое количество информации о реализованном событии 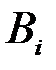. На основании полученной информации вероятности 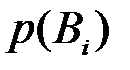могут быть переоценены по формуле Байеса, т.е. может быть вычислена апостериорная (послеопытная) вероятность 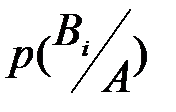события .

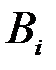Задача. Выше была задача про студента, который выучил 10 билетов из 25. Требовалось определить, в каком случае вероятность вынуть выученный билет больше, когда студент вынимает билет первым или вторым (билеты не возвращаются)? Задача была решена общим стандартным методом с построением полного пространства элементарных событий (рис. 1.2). Однако ее можно решить и с использованием формулы полной вероятности. Вероятностная диаграмма для этой задачи изображена на рис.5, где события 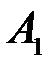и 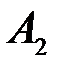состоят в том, что был вынут выученный билет соответственно при первом и втором вынимании билета; событие 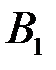- вынут невыученный билет при первом вынимании.

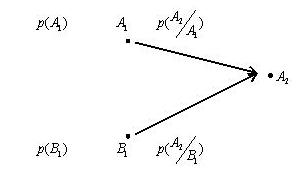
Рис.1.5. Вероятностная диаграмма

События 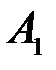и 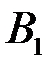образуют полную группу несовместных событий 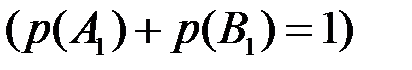. Вероятность 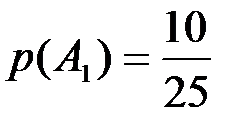вычисляется классическим методом, а вероятность 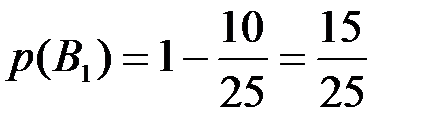. Условные вероятности вычисляются следующим образом. Появление события 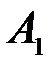изменяет комплекс условий, при котором наступает событие 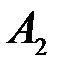, а именно: количество выученных билетов уменьшается до 9, а общее количество билетов уменьшается до 24, отсюда 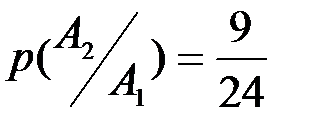. Аналогично вычисляется вероятность 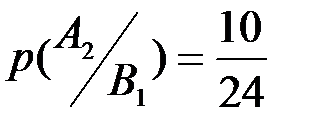. По формуле полной вероятности вероятность 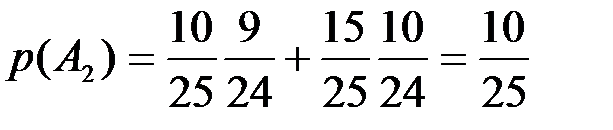. Отсюда следует, что .

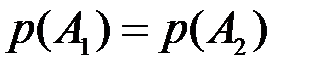Задача. Выше была решена классическим методом следующая задача. Кубик бросают два раза. С какой вероятностью при первом испытании появится единица (событие 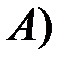при условии, что при втором испытании выпало значение больше, чем при первом (событие ).

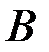Пространство элементарных событий для этой задачи изображено на рис.1.6. Эту задачу можно решить по формуле Байеса без построения полного пространства элементарных событий. В этом случае следует использовать вероятностную диаграмму.

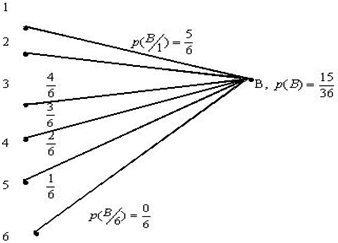Рис.1.6. Вероятностная диаграмма

Слева изображены цифры, образующие пространство элементарных событий для первого кубика. Все события равновероятны 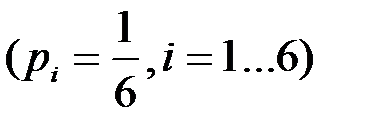. Условная вероятность 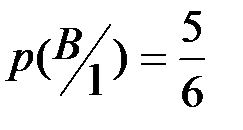события 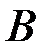вычисляется как вероятность того, что при втором испытании выпадет значение больше 1. Аналогично вычисляются остальные условные вероятности. По формуле полной вероятности находим:

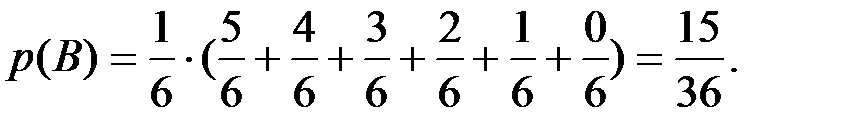
Условная вероятность 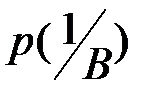вычисляется по формуле Байеса: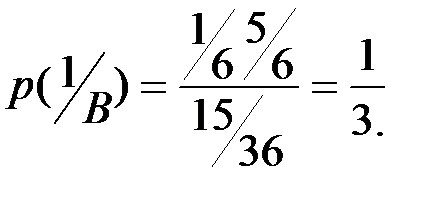

Задача. Рассмотрим пример оценки условной вероятности в случае непрерывной случайной величины. Мишень в виде круга радиуса 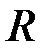можно рассматривать как пространство элементарных событий , если вероятность попасть в мишень принять равной единице (полная группа событий). Кроме этого, события можно считать несовместными, если размеры пули считать бесконечно малой величиной.

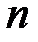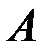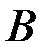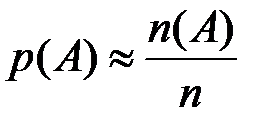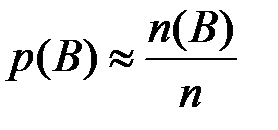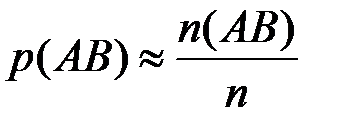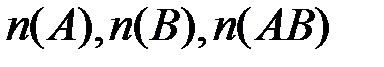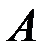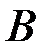Стрелок делает выстрелов, целясь в центр мишени, при этом пули будут распределены по всей мишени с некоторой плотностью, которую можно измерять количеством пуль (или весом пуль, поскольку все пули имеют одинаковый вес) приходящим на единицу площади. Выделим в мишени две фигуры (события) и , и оценим вероятности их поражения. Очевидно, , , , где -количество пуль, попавших соответственно в , в и в 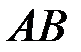- пересечение событи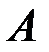й и 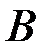. В частности, значение вероятности можно интерпретировать как вес соответствующего события по отношению к весу всего пространства , равному .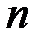

Кроме этого, можно ввести условную вероятность 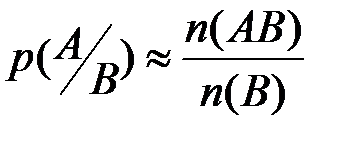, т.е. вес события 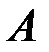, которое появляется вместе с 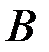(вес пересечения 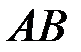) по отношению к весу события 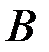. Аналогично .

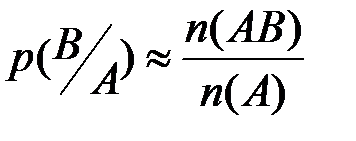Для условной вероятности 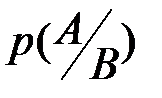подмножество 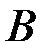является пространством элементарных событий с плотностью распределения вероятностей, равной 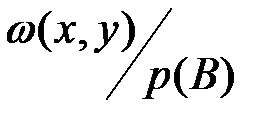, где 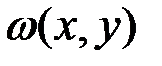- плотность распределения вероятностей в пространстве . Благодаря делению на 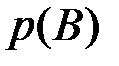подмножество 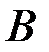становится полной группой событий. Устойчивость относительной частоты 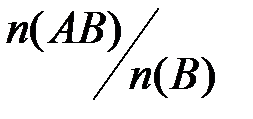появления события 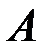при условии 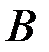является эмпирическим основанием для введения по аксиоме Колмогорова понятия условной вероятности 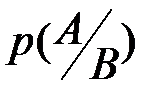. Поскольку 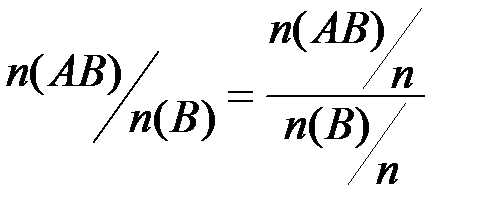, то, заменяя относительные частоты соответствующими вероятностями, получим 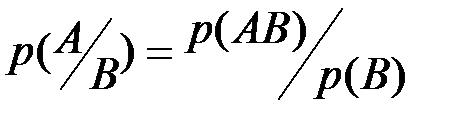, 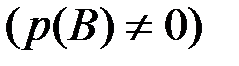и аналогично 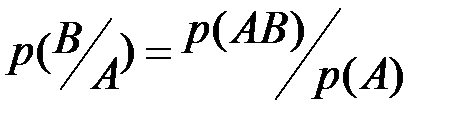( 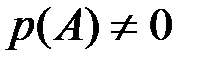). Отсюда очевидной становится формула умножения вероятностей: .

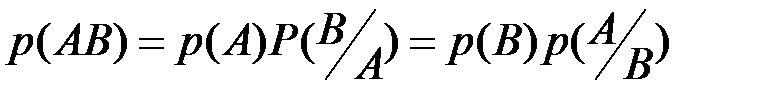Если имеет место равномерный закон распределения вероятностей в подмножестве 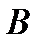, то значение вероятности 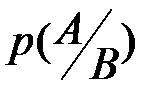можно вычислить как отношение площади пересечения событи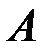й и 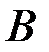к площади .

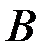Задача. Известно, что в результате 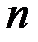испытаний событие 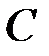появилось один раз. Какова вероятность того, что оно появилось при втором испытании? Вероятность появления события 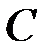при отдельном испытании равна .

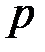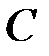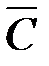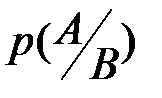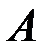Решение. Пространство элементарных событий для одного испытания состоит из событий и , которые в дальнейшем заменим соответственно на 1 и 0, а пространство элементарных событий для опыта состоит из 2ⁿ последовательностей. Необходимо вычислить условную вероятность , где ^_ событие, состоящее в том, что в результате опыта появится последовательность, содержащая единицу на втором месте. Это подмножество последовательностей, каждая из которых содержит 1 на втором месте. 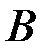^_ событие, состоящее в том, что последовательность будет содержать одну единицу. Пересечение событи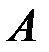й и 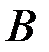состоит из единственной последовательности 010000…0. Все 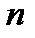последовательностей в 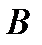равновероятны, поскольку вероятность каждой из них равна 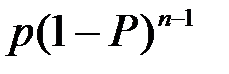, так как испытания независимы. Поэтому применим классический метод вычисления вероятностей, согласно которому .

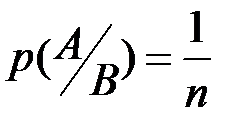Закон распределения Релея

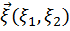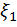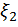Пусть имеется вектор . Координаты и – независимые центрированные случайные величины с одинаковым гауссовым законом распределения. Тогда двумерное распределение

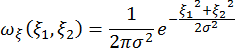
Определим плотность распределения амплитуды а и фазы φ вектора с координатам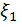и и .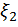

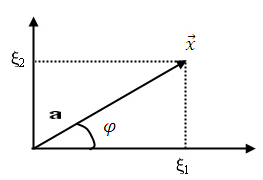
Рис. 1.10. Геометрическая интерпретация нелинейного преобразования

1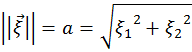

1 =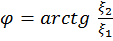

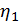
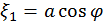
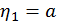
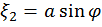
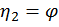
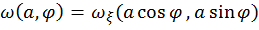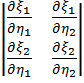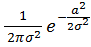|det | =

= |det ;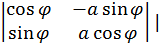

,

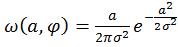0 , .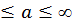

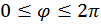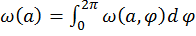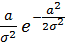= - закон распределения Релея.

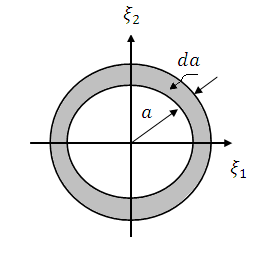
Рис. 1.11. Геометрическая интерпретация закона Релея

Вероятность 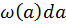равна вероятности того, что конец вектора 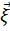попадет в кольцо с шириной, равной 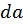и радиусом, равным 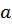(рис. 1.11).

Аналогично находится плотность распределения вероятностей фазы:

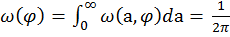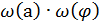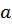. Поскольку , то и 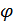независимые случайные величины.

Вероятность 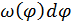равна вероятности того, что конец вектора 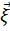попадет в конус с углом, равным .

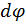Этот результат широко используется при анализе узкополосного нормального шума.

Рассмотрим ещё один пример нелинейного преобразования. Пусть случайная величина 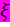имеет закон распределения Релея

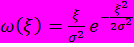при и нулю при

Нелинейное преобразование задается функцией .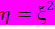

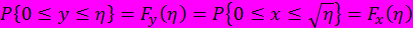, где у и х – реализации случайных величин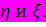

Здесь область определяется неравенством 0<ξ< 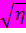а область 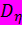- интервалом (0, 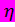) (рис. 1.12).

Из равенства = следует:

= = ,

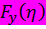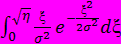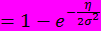И

1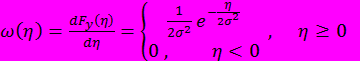

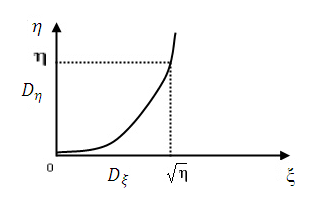
Рис. 1.12. Нелинейное преобразование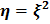

1.6.2. Геометрическая интерпретация нелинейного преобразования случайной величины.

На практике функцию g(x), которая описывает нелинейное преобразование, удобно аппроксимировать линейно-ломаной функцией, которая представляет собой последовательность отрезков разной длины, при этом точность аппроксимации повышается с уменьшением длин отрезков (рис. 1.13).

Таким образом, нелинейное преобразование можно аппроксимировать последовательностью линейных преобразований, каждое из которых отображает некоторую область на оси х в соответствую область на оси у, например, интервал [a b] – в интервал [d c] (рис. 1.13).

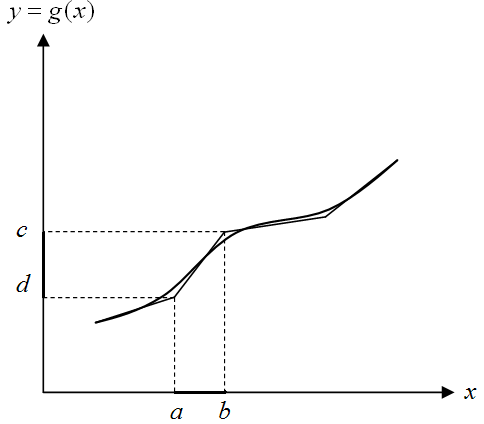
Рис. 1.13. Аппроксимация нелинейной функции g(x) линейно-ломаной функцией

Некоторые особенности линейного преобразования проявляются в зависимости от расположения отрезка: горизонтального, вертикального и под некоторым углом. Эти особенности рассмотрим на конкретных примерах.

в)

б)

а)

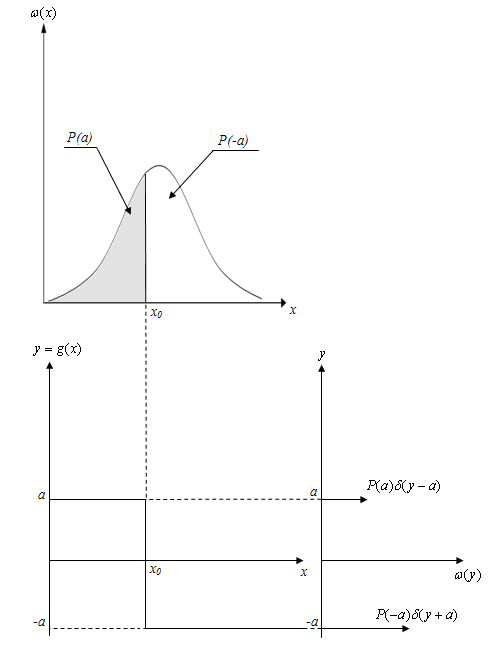
Рис. 1.14. Геометрическое представление нелинейного преобразования случайной величины

а) Исходный закон распределения; б) нелинейное преобразование в виде z-функции; в) закон распределения случайной величины у, полученной в результате нелинейного преобразования

На рис. 1.14 продемонстрирован процесс нелинейного преобразования непрерывной случайной величины х в дискретную случайную величину .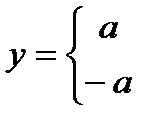

В этом случае вероятность p(-a) = p(x₀<x), а вероятность p(a) = p(x<x₀), при этом вероятность p(x₀<x) равна площади под плотностью распределения 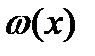правее x₀, а вероятность p(x<x₀) – левее x₀.

Закон распределения дискретной случайной величины можно описать в виде плотности распределения вероятностей, если воспользоваться дельта-функцией: 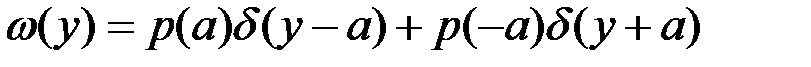, где дельта функция

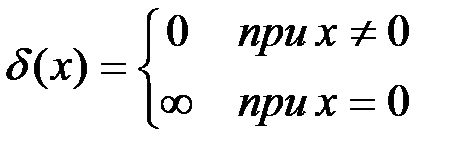и .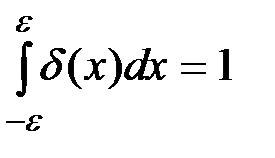

Геометрически δ-функция изображается стрелкой.

Дельта-функцию можно рассматривать как предел последовательности функций, площадь под которыми всегда равна единице, а значение в точке x=0 неограниченно растет. В частном случае δ-функцию можно получить как предел функции, изображенной на рис. , где значение ε является ее параметром.

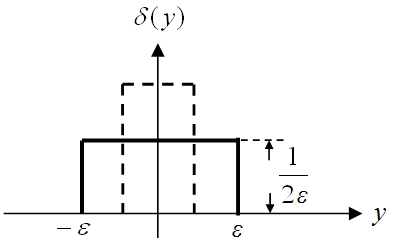
Рис. 1.15. δ-функция ______

При стремлении значения ε к нулю в пределе получается δ-функция.

Таким образом, наличие горизонтальных участков в линейно-ломаной функции всегда приводит к появлению δ-функций в плотности распределения преобразованной случайной величины.

Рассмотрим преобразование случайной величины, линейно-ломаная функция которого содержит отрезок, расположенный под некоторым углом (рис. 1.16)

в)

б)

а)

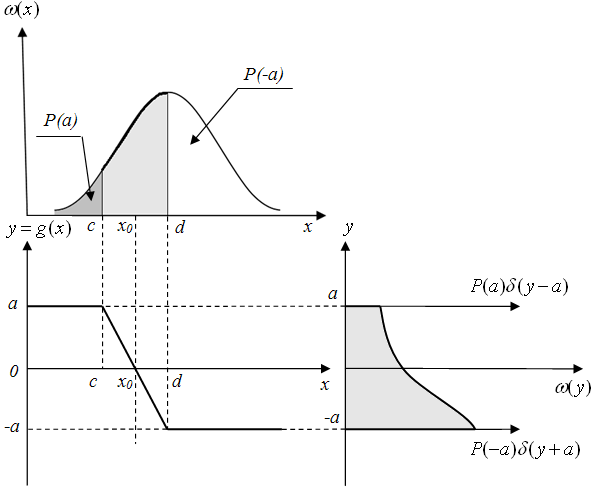
Рис. 1.16. Геометрическое представление нелинейного преобразования случайной величины

а) Исходный закон распределения; б) нелинейное преобразование; в) закон распределения случайной величины у, полученной в результате нелинейного преобразования)

В этом случае вероятность 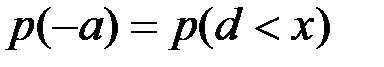, а вероятность 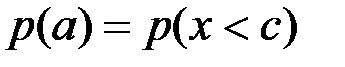. Случайная величина х на интервале [c,d] преобразуется линейно с масштабным коэффициентом k, равным 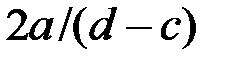, при этом вероятностная мера интервала [c,d] сохраняется, то есть площадь под плотностью 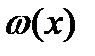на интервале [c,d]равна площади под плотностью 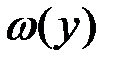на интервале [-a,a]. Если масштабный коэффициент равен единице 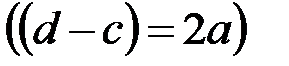, то плотност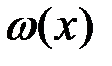и и 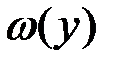на этих интервалах совпадают при положительном значении тангенса угла наклона отрезка, а при отрицательном – совпадают плотност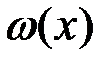и и .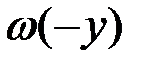

Таким образом, если длина интервала, равная 2а, увеличивается в k раз по сравнению с интервалом, равным (d-c), то во столько же раз уменьшается масштабный коэффициент по оси 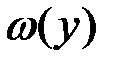, что обеспечивает сохранение вероятностной меры.

Рассмотрим случай, когда линейно-ломаная функция содержит отрезок с вертикальным расположением (рис. 1.17)

а)

б)

в)

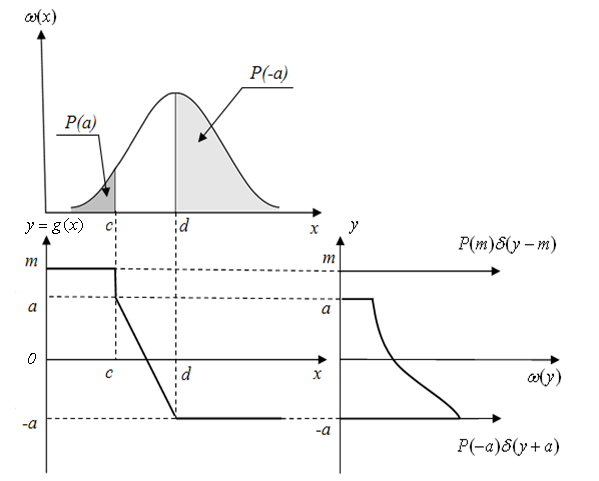
Рис. 1.17. Геометрическое представление нелинейного преобразования случайной величины (линейно-ломаная функция содержит отрезок с вертикальным расположением)

а) Исходный закон распределения, б) нелинейное преобразование; в) закон распределения случайной величины у; полученной в результате нелинейного преобразования)

Этот пример отличается от предыдущего только переносом δ-функции из точки a в точку m, при этом вероятностная мера отрезка (a, m) равна 0, поскольку он является отображением всего одной точки с вероятностной мерой, равной нулю.

В предыдущих примерах линейные преобразования считались взаимно- однозначными. Рассмотрим пример с взаимно-неоднозначным преобразованием (рис. 1.18).

в)

б)

а)

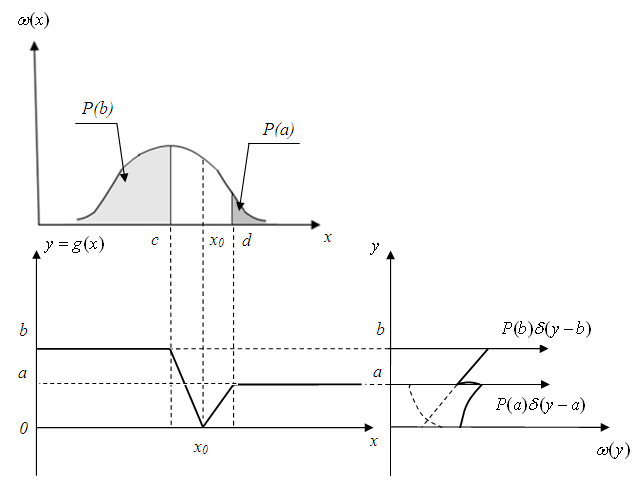
Рис. 1.18. Пример нелинейного взаимно-неоднозначного преобразования случайной величины

а) Исходный закон распределения, б) нелинейное взаимно-неоднозначное преобразование, в) закон распределения случайной величины у, полученной в результате нелинейного взаимно-неоднозначного преобразования)

В этом случае нелинейное преобразование необходимо представить в виде двух взаимно-однозначных преобразований, правее точки x₀ и левее, и для каждого из них в отдельности получить результат преобразования. Окончательный результат получается как сумма отдельных результатов, поскольку события правее x₀ и левее x₀ несовместны. Окончательный результат изображен сплошной линией.

Функция регрессии.

Линейная функция регрессия.

В некоторых случаях вводится ограничение на вид возможных функций 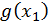, например, ограничиваются классом линейных функций 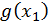, которые записываются в виде 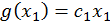+ 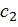. Выбор оптимальной функции из этого класса, т.е. той, которая дает оценку с минимальной среднеквадратической ошибкой, сводится к определению коэффициентов .

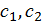Функция 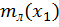= 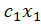+ 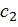, для которой среднеквадратическая ошибка

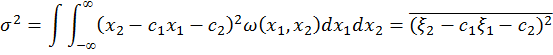
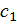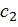минимальна, называется функцией линейной регрессии, а соответствующие коэффициенты и – коэффициентами регрессии.

Обозначив через 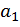и 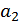средние значения случайных величин 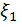и 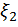, коэффициенты регрессии можно определить, если сделать следующие тождественные преобразования:

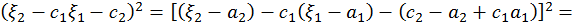
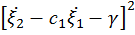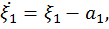
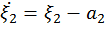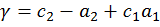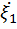, где , , и 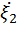- центрированные случайные величины.

Тогда 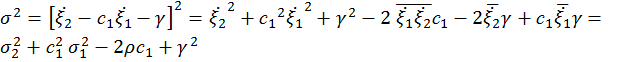, (1.2)

где 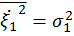и 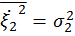по определению дисперсии случайных величин 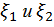, 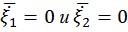как среднее значение от центрированных случайных величин.

= –

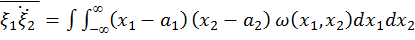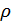среднее от произведения двух центрированных случайных величин 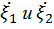называется корреляцией между этими случайными величинами. Иногда удобнее использовать коэффициент корреляции r = 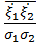= 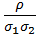, который определяется как среднее значение от произведения центрированных и нормированных случайных величин 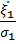и .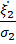

С учетом введенных обозначений можно произвести следующие тождественные преобразования выражения (1.2):