Метод наименьших квадратов для однофакторной модели.

Допустимое значение y связано с координатами x уравнением вида:

Имеем ряд значений:

N	x	y
	-2
	-1

Необходимый расчет коэффициентов в однофакторной модели.

Система нормальный уравнений для однофакторного случая будет иметь вид:

Если все подсчитать, то получится: b₀=2, b₁=1 → получаем уравнение:

Запишем в матричной форме. Имеем 3 упорядоченных множества:

Первое – множество условного опыта

Второе – результат опыта

Третье – коэффициенты

; ;

Все элементы приведенных матриц упорядоченные: X и Y - по номерам опытов, B - по номерам коэффициентов, которые соответствуют номерам элементов, на основании исходных данных систему из пяти уравнений можно записать в матричном виде:

Размеры должны быть согласованные.

Система квадратных уравнений методом наименьших квадратов имеет вид:

В матричном виде она будет как:

Умножим обе части на X^T:

Для полученной системы нормальных уравнений нужно произведение матриц умножить на , которая представляет собой матрицу условий опыта, в которой поменяли местами столбцы и строки.

Не все матрицы имеют обратную.

Взвешенный метод наименьших квадратов

Статистический анализ

Дублирование опытов повышает точность эксперимента данных и надежность полученных моделей.

Различают равномерное и неравномерное дублирование.

Равномерное дублирование – это когда в каждой точке плана производится одинаковое число опытов, то есть каждой строчке плана соответствует одинаковое число значение у_i.

Если не делать различия между этими значениями, то это эквивалентно увеличению числа строк в матрице «весов»

P=En

Е- единичная матрица

n- число измерений в каждой точке

P=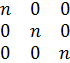

С учетом матрицы весов решение системы нормальных уравнений имеет вид

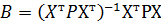
Для дисперсии адекватности

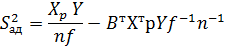
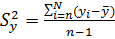дисперсия воспроизводимости.

Проверяется значимость коэффициентов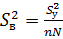

Таким образом, для случая статического анализа коэффициентов с равнопеременным дублированием опыта применяется та же схема обработки результатов, но учитывающая усреднение значения У.

Определим дисперсию адекватности и дисперсии коэффициентов, значимость коэффициентов уравнения регрессии.

Глава 9. Принятие решений после построения моделей.

Интерпретация результатов

Получено уравнение регрессии у=f(x_i)

Y=b₀+b₁x₁+b₂x₂+…+b_kx_k+b_k+1x₁x₂+…+b_k+m(x_k-1x_k)

1.Учет знаков при коэффициенте max

Интерпретация моде зависит от того, что мы определяем max или min функции y

2. Учитывается величина коэффициентов.

Их надо учитывать по силе воздействия на функцию отклика b₂>b

Статистически не значимые факторы не рассматриваются. Следует учесть, что изменение интервалов варьируется, приводит к изменению коэффициентов регрессии, так как величина коэффициента пропорциональна соответствующему интервалу варьирования |b_i|~|I_i|

Но коэффициенты могут изменять знак на обратный, если в ходе эксперимента случайно прошли max.

3. Построение уравнения регрессии для натуральных значений факторов. При этом изменяется величина всех коэффициентов и исчезает возможность их сравнения по величине.

Интерпретация взаимодействий неоднозначна, так как необходимо учитывать знаки основных эффектов. Причем если они различны, то следует исключить самый сложный эффект

y=b₀+b₁x₁+...