Дробный факторный эксперимент.
С увеличением числа факторов резко возрастает число точек плана, а следовательно число опытов, поэтому полный факторный план практически не применяется при к 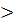 6, главная задача организация экспериментального исследования – это сокращение числа опытов для этого применяют дробные факторные планы вида ДФЭ2к-m (дробный факторный эксперимент).
6, главная задача организация экспериментального исследования – это сокращение числа опытов для этого применяют дробные факторные планы вида ДФЭ2к-m (дробный факторный эксперимент).
Всякий факторный план, который содержит меньшее число факторов, чем полный план, называют дробным экспериментом или репликой.
Если число опытов в реплике кратно число уровней факторов, то реплика называется регулярной, иначе нерегулярной.
Пусть двухфакторный план и к=6, тогда полный факторный эксперимент 26=64, поэтому дробный факторный эксперимент 26-1=32, дробный факторный эксперимент 26-2=16.
Минимальная регулярная реплика.
В двухуровневом факторном плане число линейных эффектов равно l=к+1, поэтому минимальное число опытов в дробном факторном плане N=2к-m  l=к+1, пролагорифмируем и получим
l=к+1, пролагорифмируем и получим
к-m 
m 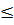 к-
к-  ,
,
причем к и m – целые числа.
Генератор плана.
Возникает вопрос: «как формализовать выбор реплики?»
ПФЭ2k N=2k
ДФЭ2k-m N'=2k-m
Если k=3, то N=23=8
| N | X1 | X2 | X3 | Yi |
| - | - | - | Y1 | |
| + | - | - | Y2 | |
| - | + | - | Y3 | |
| + | + | - | Y4 | |
| - | - | + | Y5 | |
| + | - | + | Y6 | |
| - | + | + | Y7 | |
| + | + | + | Y8 |

ДФЭ2k-m если k=3, то m=1 → N=4
Генератор плана: x3=x1∙x2 или x3’= - x1∙x2
| N | X1 | X2 | X3 |
| - | - | + | |
| + | - | - | |
| - | + | - | |
| + | + | + |
| N | X1 | X2 | X3 |
| - | - | - | |
| + | - | + | |
| - | + | + | |
| + | + | - |
Смешивание эффектов.
Определяющий контраст.
Для построения первой реплики трехфакторного эксперимента мы воспользовались генератором плана вида x3=x1∙x2 , но квадрат фактора x3∙ x3=│ x3│= 1 = x1∙x2∙ x3, это значение принято называть определяющий контраст (I).
I = x1∙x2∙ x3 ≡ 1
С помощью определяющего контраста можно определить какие оценки полной факторной модели содержат смешивание эффектов.
Полный факторный план позволяет построить модель вида:
Y = b0+b1x1+b2x2+b3x3+b12x1x2+b13x1x3+b23x2x3+b123x1x2x3
A ДФЭ23-1 : Yʹ = b0’+b1’∙x1+ b2’∙x2+ b3’∙x3
Поэтому коэффициенты ДФЭ содержат в себе коэффициенты или оценки коэффициентов ПФЭ. Определить смешивание эффектов можно с помощью определяющего контраста плана.
b0’ = b0x0+ b123x1x2x3
b0’ = b0+ b123
b1’= b1+ b23
b2’= b2+ b13
b3’= b3+ b12
К сожалению все значительно усложняется при увеличении количества факторов.
Построение ДФЭ для четырех факторов (k=4)(1/2 реплики)
K=4
в ПФЭ N=24=16
в ДФЭ Nʹ=24-1=16
| N | b0 | b1 | b2 | b3 | b4 |
| x0 | x1 | x2 | x3 | x4 | |
| - | - | - | - | ||
| + | - | + | + | ||
| - | + | - | + | ||
| + | + | - | - | ||
| - | - | + | + | ||
| + | - | + | - | ||
| - | + | + | - | ||
| + | + | + | + |
x4 = x1x2x3
b0’ = b0+ b1234
b1’= b1+ b234
b2’= b2+ b134
b3’= b3+ b124
b3’= b3+ b124
b4’= b4+ b123
b12’= b12+ b34
b13’= b13+ b24
b23’= b23+ b14
Составление ДФЭ для 5,6,и 7 факторного эксперимента.
Порядок минимальной регулярной реплики для этих планов можно записать в следующем виде:
k = 5, то m=2 → N= 25-2=8 (1/4 реплика)
k = 6, то m=3 → N= 26-3=8 (1/8 реплика)
k = 7, то m=4 → N= 27-4=8 (1/16 реплика)
Т.е. мы можем проведя всего восемь опытов построить дробный факторный план и получить оценки модели для числа факторов до 7. Причем чем больше число факторов, тем больше должно быть число генератора плана, т.е. для каждого фактора нужно придумать генератор плана.
Для k=5 нужно генератор плана для x4 и x5=x1x2
k=6 → x4, x5, x6= x1x3
k=7 → x4, x5, x6, x7= x2x3
Глава 6 Проведение эксперимента.
Основной уровень фактора.
Основной уровень фактора, т. е. его начальное значение, с которого начинается эксперимент для его выбора необходим анализ априорной информации.
Начальный уровень фактора должен был располагаться в области определения факторов, таким образом, чтобы сочетание факторов не приводили к появлению нежелательных эффектов или к нарушению технологических режимов. Нормированное значение уровня фактора принимается равное нулю, т.е.
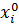 =0
=0
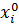 =
= 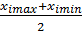
Шаг изменения фактора.
Это величина, на которую изменяют фактор от опыта к опыту, т.е. интервал дискретности фактора.
Внутри шага фактор не может принимать значения, величина шага выбирается с учетом двух противоположных факторов (условий):
1. Увеличение шага, уменьшает содержательность и точность модели.
2. Уменьшение шага, увеличивает число опытов и стоимость эксперимента.
Шаг изменения фактора должен быть больше разрешающей способности измерительных приборов, и определяется возможностью изготовления образцов с заданной точностью. Т.е. желательно знать заранее, сколько образцов можно (изготовить) провести, каким временем располагаем: интервал варьирования равен половине рабочего диапазона.
Изменение фактора:
Јi = 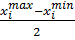 ,
,
Интервал варьирования определяет возможные изменения фактора и диапазона, в которых происходит исследования.
Начальный уровень фактора, интервал варьирования и шаг на каждом этапе эксперимента неизменны, и только на завершающем этапе исследования (при построении нелинейной модели) можно изменить эти величины.
Если при движении в факторном пространстве, значения какого либо фактора достигают границу области определения, то этот фактор исключается из рассмотрения, фиксируя его на граничном уровне.
Рандомизация.
Рандомизация заключается в случайном расположении точек плана, т.е. последовательности выполнения опытов в соответствии с оптимальным планом.
В следующей системе все факторы можно разделить на две группы:
I группа: изучаемые факторы это x1x2x3
II группа: мешающие факторы (помехи) влияние, которых мы не учитываем в эксперименте.
Для исключения влияния факторов II группы и применятся рандомизация.
| n | x1 | x2 | x3 | y |
| - | - | - | y1+ε | |
| + | - | - | y2+ε | |
| - | + | - | y3+ε | |
| + | + | - | y4+ε | |
| - | - | + | y5+ε | |
| + | - | + | y6+ε | |
| - | + | + | y7+ε | |
| + | + | + | y8+ε |
n число опытов
ε ошибка (не учитываем)
Допустим для 3 опыта
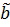 3=
3=  (-4ε+
(-4ε+ 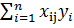 )=b3-
)=b3-  ε.
ε.
Вычисление оценок.
Для ортогонального плана, вычисления соответствующих оценок производится по формуле
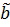 j=
j= 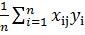 ,
,
т.е. равны суммам произведений откликов на элементы соответствующего столбца плана.
При вычислении оценок необходимо соблюдать высокую точность вычислений (не менее 4 знаков после запятой) округление допускается только конечного результата.
Для контроля правильности вычислений необходимо рассчитать следующие суммы:
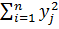
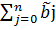 2
2
Теоретически должно выполняться соотношение
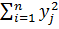 =N
=N 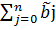 2
2
Из-за округлений в процессе вычисления накапливаются ошибки и возможны отклонения от этой формулы
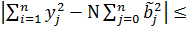 0,1
0,1 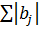
Если это выполняется, то считаем что вычисления выполнены верно и не содержат ошибок.
Глава 7.
Регрессионный анализ.
Цель регрессионного анализа – проверка адекватности полученной модели, проверка значимости оценок коэффициентов модели.
Поставленная цель достигается при следующих допущениях:
1. Параметр оптимизации Y является случайной величиной с нормальным законом распределения.
2. Дисперсия Y не зависит от величины Y, т.е. постулируется однородность дисперсий в различных точках факторного пространства.
3. Значение факторов не является случайными величинами, т.е. имеется возможность устанавливать каждый фактор на определенном уровне, точнее чем ошибка воспроизведения.
