Принцип наименьших квадратов.
На основании определенного массива экспериментальных данных построим модель:
Y=Ф(Х)
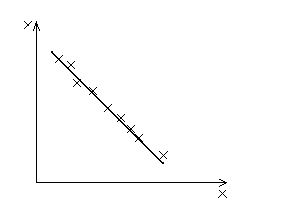
y=b0+b1x1
Установим насколько точно данная модель описывает экспериментальные результаты.
В качестве критерия, который характеризует достоверность или адекватность модели можно выбрать такой, который обеспечивал бы min-е значение некоторой величины.
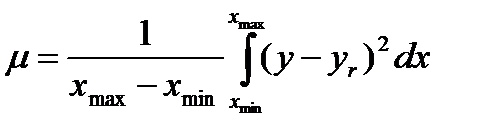
y – это функция, которая описывает состояние модели
(y-yr) – определяет отклонение модели от реальных результатов.
В качестве меры такого отклонения выбирают min- четную функцию, то есть (y-yr)2. Для дискретных величин параметр адекватности будет представлен в виде:
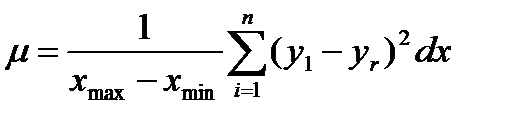
Таким образом из принципа наименьших квадратов следует метод наименьших квадратов.
Обобщенная дисперсия.
Допустим имеется несколько случайных величин х, которые распределены на множестве Х с некоторой дисперсией Д(х).
Величина дисперсии, …. оценка дисперсии
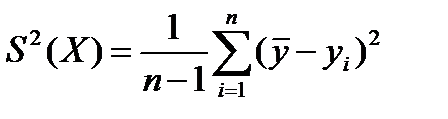
Если имеются два объекта, которые характеризуются соответствующими дисперсиями Д1(х) и Д2(х) и между этими величинами (объектами) наблюдается взаимозависимость, тогда вводится понятие о коэффициентах корреляции r(x1,x2), причем
|r(x1,x2)| <1
Коэффициент корреляции характеризует степень линейной зависимости одной величины от другой. Для любой функции коэффициент корреляции будет представлять отношение линейной части функции ко всему его значению
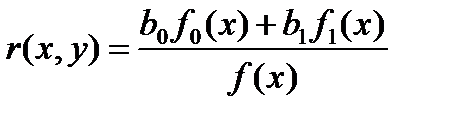
Ковариации между случайными величинами х1 и х2 называют следующие произведение:
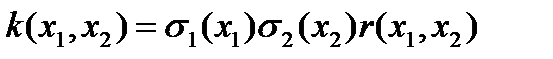
Причем 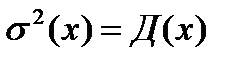
Таким образом, случайные величины характеризуются следующими числами
- дисперсией 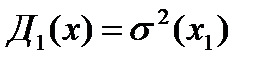
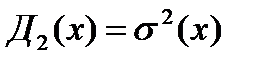
- ковариацией k= (x1,x2)
Для выборочных оценок можем записать
-для дисперсии
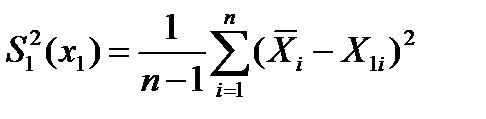
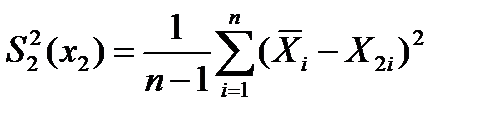
-для корреляции
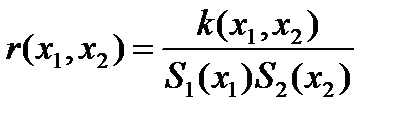
-ковариация
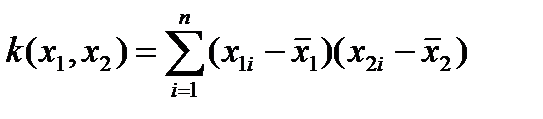
Корреляционная матрица
Это такая матрица, на главной диагонали которой находится соответствующие дисперсии, а остальные коэффициенты представляют ковариации соответствующих величин.
Определитель такой матрицы представляет собой обобщенную дисперсию.
Обобщенная дисперсия является характеристикой точности математической модели, поэтому планы, которые min-т обобщенную дисперсию называют деоптимальными планами.
Метод наименьших квадратов в большинстве случаев обеспечивает оптимальность модели.
Построение оптимальных планов
П1 Нормирование факторов
Все планы составляют для нормированных значений факторов, т.е. максимальному значению уровня, фактору присваивают +1, минимальному -1, центр плана при этом равен нулю.
Вычисление оценок коэффициентов и проверка адекватности модели производится также в нормированных величинах, но интерпретация полученных результатов модели проводится только в реальных значениях факторов.
y=b0+b1x1+b2x2….
y=a0+a1g(c)+a2g(Ni)….
Обозначим через Xн - нормированное значение фактора,
Xр – реальное значение фактора.
Тогда для перехода к нормированным значениям справедлива формула
Xн= 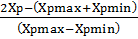
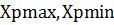 - верхний и нижний уровни факторов.
- верхний и нижний уровни факторов.
Xр=1/2( 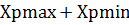 )+Xн(
)+Xн( 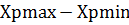 )
)
Структура оптимальных планов.
Она определяется теоремой Кифера, которая гласит, что для n-наблюдений, когда факторы нормированы и варьируются от +1 до -1, тогда наблюдение необходимо располагать равномерно в точках плана, которые являются нулями полинома Лежандра, т.е. решением уравнения
(1-x2)L'm =0
L'm – полином Лежандра,
m – степень полинома Лежандра.
Таблица оптимальных точек по теореме Кифера
| m | Точки плана на отрезке +1…-1 ( 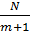 ) ) |
В каждой точке плана проводится ( 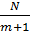 ) опытов ) опытов | |
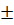 1; 1; | |
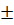 1; 0 1; 0 | |
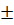 1; 1; 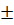 0,4272; 0,4272; | |
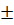 1; 1; 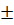 0,6547; 0; 0,6547; 0; | |
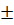 1; 1; 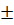 0,7651; 0,7651; 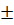 0,2852; 0,2852; | |
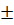 1; 1; 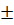 0,8302; 0,8302; 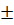 0,4689; 0; 0,4689; 0; |
1. Отсюда следует, что число точек плана находится как (m+1)
2. Оставшиеся после равномерного распределения опытов, по точкам плана необходимо размещать как можно ближе к границам изменения факторов.
Глава 5 Факторное планирование эксперимента.
5.1 Полный двухуровневый факторный план вида 2к .(ПФЭ2к)
Пусть даны два фактора x1, x2, предполагаем наличие линейной модели вида y=b0+b1x1+b2x2+b12x1x2; Оптимальный факторный план должен иметь четыре точки плана, т.е. N=2k-2=4, тогда ПФП будет иметь вид.
| n | x0 | x1 | x2 | x12 | y |
| -1 | -1 | +1 | y1 | ||
| +1 | -1 | -1 | y2 | ||
| -1 | +1 | -1 | y3 | ||
| +1 | +1 | +1 | y4 |
n - номер точки плана
x0 - нормальный фактор
y1…y4 – результаты.
Подсчитаем сумму элементов в каждом столбце. Такие планы кроме условия оптимальности являются ортогональными, т. е. позволяют рассчитывать оценки для коэффициентов моделей и обеспечивают независимость этих оценок, тогда коэффициенты модели полного факторного плана рассчитывают по формуле.
bj= 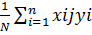
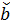 0=
0=  (y1+y2+y3+y4)
(y1+y2+y3+y4)
~ оценка
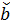 1=
1=  (-y1+y2-y3+y4)
(-y1+y2-y3+y4)
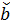 2=
2=  (-y1-y2+y3+y4)
(-y1-y2+y3+y4)
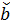 12=
12=  (y1-y2-y3+y4)
(y1-y2-y3+y4)
Таким образом находим оценки коэффициентов в уравнении регрессии после чего в любой точке факторного пространства можно найти значения параметра (величины) y в области определения факторов
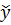 =
= 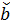 0 +
0 + 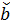 1 x1+
1 x1+ 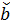 2 x2 +
2 x2 + 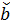 12 x1x2
12 x1x2
Для трехфакторного эксперимента, когда даны три фактора x1x2x3, построение плана вида ПФЭ2к заключается составлением таблицы позволяющих найти оценки для моделей вида
y=b0+d1x1+b2x2+b3x3+b12x1x2+b13x1x3+b23x2x3+b123x1x2x3
общее число точек плана N=2к=3=8
Построим план эксперимента
| n | x0 | x1 | x2 | x3 | x1x2 | x1x3 | x2x3 | x1x2x3 | y |
| -1 | -1 | -1 | +1 | -1 | +1 | -1 | y1 | ||
| +1 | -1 | -1 | -1 | -1 | +1 | +1 | y2 | ||
| -1 | +1 | -1 | -1 | +1 | -1 | +1 | y3 | ||
| +1 | +1 | -1 | +1 | -1 | -1 | -1 | y4 | ||
| -1 | -1 | +1 | +1 | -1 | -1 | +1 | y5 | ||
| +1 | -1 | +1 | -1 | +1 | -1 | -1 | y6 | ||
| -1 | +1 | +1 | -1 | -1 | +1 | -1 | y7 | ||
| +1 | +1 | +1 | +1 | +1 | +1 | +1 | y8 |
Оценки находятся по формуле
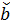 j=
j= 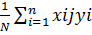
Таким образом мы можем определить оценку любого коэффициента модели по соответствующему столбцу плана, такой эксперимент, в котором реализуется все N=2к опытов называются полным факторным экспериментом, отметим в ряде случаев нет необходимости построения модели, которая учитывает все эффекты взаимодействий факторов, а можно ограничится только оценками линейных эффектов. Такая задача решается путем построения дробных факторных планов.
