Метод адиабатического расширения

МЕТОД АДИАБАТИЧЕСКОГО РАСШИРЕНИЯ

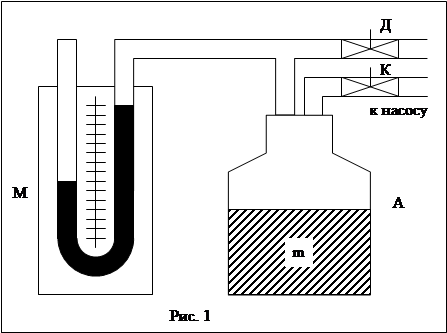(метод Клемана-Дезорма)

В сосуд А с помощью насоса накачивается воздух, создавая внутри его давление выше атмосферного так, чтобы разность уровней в манометре равнялась 15-25 см. При этом температура воздуха в со­суде сначала повысится, но через некоторое время в результате тепло­обмена сравняется с температурой окружающей среды. Воздух элементар­ного объема будет характеризоваться параметрами P₁, Т₁, V₁, что со­ответствует точке 1 на графике (рис.2). Когда давление воздуха в со­суде установилось, на короткое время соединим сосуд с атмосферой краном Д. При этом часть закаченного воздуха выйдет из сосуда. Воздух в сосуде, а значит и элементарный объем массой dm, расширят­ся. Это расширение можно считать адиабатическим, так как оно происходит быстро и теплообмен с окружающей средой практически не происходит. Давление в сосуде сравнивается с атмосферным, а темпе­ратура понизится. На, графике (рис. 2) процесс расширения изображен отрезком адиабаты 1-2. Параметры воздуха в процессе такого расши­рения связаны уравнением адиабаты (уравнение Пуассона)

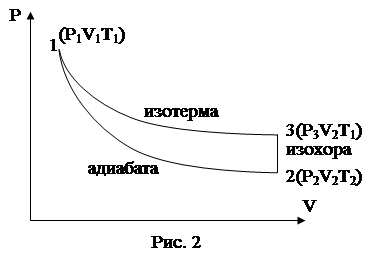P₁V₁^g = P₂V₂^g (1)

Закроем кран Д. Через 3-5 минут воздух в сосуде нагревается до температуры окружающей среды. Так как нагревание происходит практи­чески при постоянном объеме, то давление в сосуде несколько повысится. Процесс изобразится отрезком изохоры, и параметры примут значения (P₃T₁V₂) (рис. 2).

Для повторения эксперимента открываем кран Д. Элементарный объем приходит в исходное состояние 1. Процесс 3-1 (рис. 2) - изотермичес­кий процесс, процесс при температуре окружающей среды.

Для элементарной массы газа dm на основании уравнения Бойля – Мариотта имеем:

P₁V₁ = P₃V₂ (2)

Для определения показателя адиабаты возведем уравнение (2) в сте­пень g и разделим его почленно на уравнение (1)

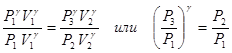(3)

Логарифмируем уравнение (3), находим:

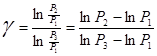(4)

Эту формулу можно упростить, исходя из условий эксперимента. Вы­разим давление воздуха в сосуде через разность уровней жидкости в манометре. Обозначим уровень, соответствующий атмосферному давлению буквой Н, добавочное давление, измеряемое разностью уровней в мано­метре, в состояние 1 - буквой h₁ и добавочное давление в состояние 3 - буквой h₂.

Тогда:

P₁ = H + h₁ ; P₂ = H ; P₃ = H + h₂

Подставим эти значения в формулу (4)

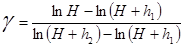
Так как атмосферное давление велико в сравнении с добавочными давлениями, то величины Н; H+h ; H+h мало отличатся друг от друга. В этом случае разность логарифмов можно принять пропорциональной разности самих чисел и приближенно положить:

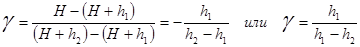(5)

Формула (5) является расчетной формулой для определения g. Весь воздух массой m, не выходящий в процессе экспериментов из со­суда А (cм. рис. 1), ведет себя так же, как и воздух в элементарном объеме.

Л И Т Е Р А Т У Р А

1. И. В. Савельев. Курс физики, М, 1989г.

2. А. А. Детлаф, Б.М.Яворский. Курс Физики. 1999г.

МЕТОД АДИАБАТИЧЕСКОГО РАСШИРЕНИЯ

(метод Клемана-Дезорма)

В сосуд А с помощью насоса накачивается воздух, создавая внутри его давление выше атмосферного так, чтобы разность уровней в манометре равнялась 15-25 см. При этом температура воздуха в со­суде сначала повысится, но через некоторое время в результате тепло­обмена сравняется с температурой окружающей среды. Воздух элементар­ного объема будет характеризоваться параметрами P₁, Т₁, V₁, что со­ответствует точке 1 на графике (рис.2). Когда давление воздуха в со­суде установилось, на короткое время соединим сосуд с атмосферой краном Д. При этом часть закаченного воздуха выйдет из сосуда. Воздух в сосуде, а значит и элементарный объем массой dm, расширят­ся. Это расширение можно считать адиабатическим, так как оно происходит быстро и теплообмен с окружающей средой практически не происходит. Давление в сосуде сравнивается с атмосферным, а темпе­ратура понизится. На, графике (рис. 2) процесс расширения изображен отрезком адиабаты 1-2. Параметры воздуха в процессе такого расши­рения связаны уравнением адиабаты (уравнение Пуассона)

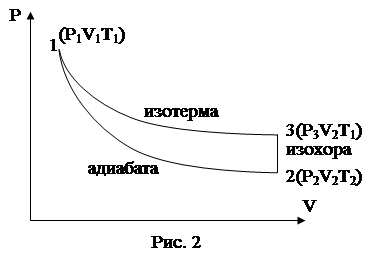P₁V₁^g = P₂V₂^g (1)

Закроем кран Д. Через 3-5 минут воздух в сосуде нагревается до температуры окружающей среды. Так как нагревание происходит практи­чески при постоянном объеме, то давление в сосуде несколько повысится. Процесс изобразится отрезком изохоры, и параметры примут значения (P₃T₁V₂) (рис. 2).

Для повторения эксперимента открываем кран Д. Элементарный объем приходит в исходное состояние 1. Процесс 3-1 (рис. 2) - изотермичес­кий процесс, процесс при температуре окружающей среды.

Для элементарной массы газа dm на основании уравнения Бойля – Мариотта имеем:

P₁V₁ = P₃V₂ (2)

Для определения показателя адиабаты возведем уравнение (2) в сте­пень g и разделим его почленно на уравнение (1)

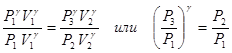(3)

Логарифмируем уравнение (3), находим:

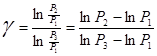(4)

Эту формулу можно упростить, исходя из условий эксперимента. Вы­разим давление воздуха в сосуде через разность уровней жидкости в манометре. Обозначим уровень, соответствующий атмосферному давлению буквой Н, добавочное давление, измеряемое разностью уровней в мано­метре, в состояние 1 - буквой h₁ и добавочное давление в состояние 3 - буквой h₂.

Тогда:

P₁ = H + h₁ ; P₂ = H ; P₃ = H + h₂

Подставим эти значения в формулу (4)

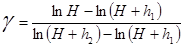
Так как атмосферное давление велико в сравнении с добавочными давлениями, то величины Н; H+h ; H+h мало отличатся друг от друга. В этом случае разность логарифмов можно принять пропорциональной разности самих чисел и приближенно положить:

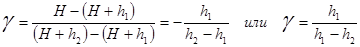(5)

Формула (5) является расчетной формулой для определения g. Весь воздух массой m, не выходящий в процессе экспериментов из со­суда А (cм. рис. 1), ведет себя так же, как и воздух в элементарном объеме.