Тема 7. Исследование активных фильтров

Цель работы:Изучение фильтров низких и высоких частот.

Теория и примеры выполнения задания.

Усилители, имеющие избирательные свойства, условно подразделяют на фильтры низких и высоких частот, а также полосовые и режекторные (заграждающие). Фильтры низких и высоких частот соответственно пропускают только низкие или только высокие частоты, полосовые и режекторные обеспечивают пропускание и непропускание сигналов определённых частот.

Для получения у усилителей избирательных свойств в области низких частот (ниже 20 кГц) преимущественно применяют RC-цепи интегрирующего или дифференцирующего типа. Они включаются на входе или выходе дифференцирующего типа. Они включаются на входе или выходе усилителя и охватывают его частотно-зависимой обратной связью.

В области высоких частот в качестве фильтров низких частот широко применяют высокочастотные дроссели, а полосовые и режекторные фильтры выполняют на основе использования катушек индуктивности (LC-фильтры).

В отдельных случаях применяют электромеханические фильтры, которые относятся к числу полосовых и имеют резонансную частоту, равную частоте собственных механических колебаний системы. Добротность таких фильтров обычно высокая (сотни - тысячи единиц), но перестройка частоты затруднена. Поэтому электромеханические фильтры в основном применяют в технике связи или радиовещании, где имеются стандартные определённые рабочие частоты.

Под активными фильтрами обычно принимают электронные усилители, содержащие RC-цепи, включенные так, что у усилителя появляются избирательные свойства. При их применении удаётся обойтись без громоздких, дорогостоящих и нетехнологичных катушек индуктивности и создать низкочастотные фильтры в микроэлектронном исполнении, в которых основные параметры могут быть изменены с помощью навесных резисторов и конденсаторов.

К характеристикам фильтров относятся: 1) передаточная функция, 2) амплитудно-частотая характеристика, 3) фазочастотная характеристика, 4 ) частота среза ωср ( fср), 5) постоянная времени τ, 6) полоса пропускания (подавления) Δω (Δf), 7) резонансная частота, 8) добротность Q.

Передаточная функция это отношение изображения по Лапласу выходной величинык изображению по Лапласу входной величины фильтра.

K(p) = L(Uвых (t))/L(Uвх (t) .

В общем случае фильтр можно рассматривать как четырехполюсник с передаточной функцией

K(p) = U2(p) / U1(p) = (a_m p^m + a_m-1p^m-1 + ... + a₁p + a₀) / (b_m p^m + b_m-1p^m-1 + ... +bp + b₀),

где U1(p) и U2(p) – входное и выходное напряжение четырехполюсника в операторной форме; a и b – вещественные постоянные величины; m, n = 1, 2, 3, ... ; n – определяет порядок фильтра.

Для установившейся частоты p = jω и передаточную функцию можно првести к виду

K(p) = U2(jω) / U1(jω) = (a_m ( jω) ^m + a_m-1( jω)^m-1 + ... + a₁( jω) + a₀) / (b_m ( jω)^m + b_m-1( jω)^m-1 + ... +b( jω) + b₀),

Модуль этой переключательной функции называется амплитудно-частотной характеристикой.

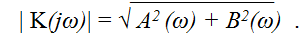
Фазо-частотная характеристика также может быть найдена из выражения для K(p) и представлена в виде φ(ω) = arctg (B(ω) / A(ω)).

Диапазон Δω = ω2 – ω1 или полосы частот, в которых проходят сигналы, называются полосами пропускания. В полосе пропускания значение коэффициента передачи относительно велико, а в идеальном случае постоянно. Для полосового фильтра частоты ω2 и ω1 определяются при спаде коэффициента передачи на 3 дБ

Диапазон частот Δω = ω2 – ω1, в которых сигналы подавляются, образуют полосу задержания. В

полосе задержания коэффициент передачи фильтра относительно мал, а в идеальном случае равен нулю. Для заграждающего фильтра частоты ω2 и ω1 определяются при спаде коэффициента передачи на 3 дБ.

Частота среза ωср (fср) – частота, на которой наблюдается спад коэффициента передачи на 3 дБ по сравнению с с коэффицинтом передачи на нулевой ( для ФНЧ ) или бесконечной ( для ФВЧ ) частоте.

Резонансная частота fP – частота, на которой коэффициент передачи фильтра имеет максимальное значение (для полосового фильтра) или минимальное значение (для заграждающего фильтра).

Добротность Q – добротность полосового фильтра определяется как отношение резонансной частоты к полосе пропускания Q = f_p / (ω2 – ω1).

Простейшие фильтры высоких и низких частот показаны на рис.7.1,а,в. В них конденсатор, определяющий частотную характеристику, включён в цепь ОС.

Для фильтра высоких частот, который часто используется в качестве дифференцирующего устройства, коэффициент передачи

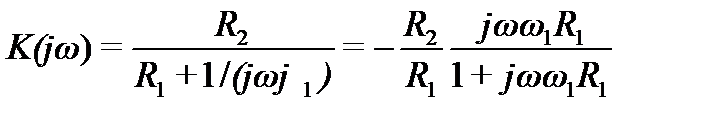
Переходя к операторной записи, получим передаточную функцию

,

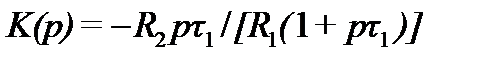где .

ЛАЧХ данного фильтра приведена на рис.220,б. Частоту сопряжения асимптот , откуда

Установившейся частоты.

Для фильтра низких частот (рис. 7.1,в) аналогично рассмотренному имеем

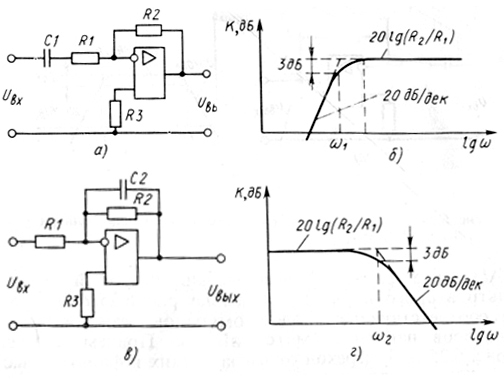
Рисунок 7.1 – Структура и характеристики фильтра низких частот.

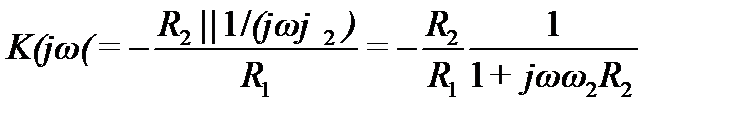
или в операторном виде

,

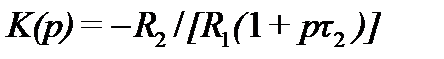где .

ЛАЧХ фильтра низких частот показана на рис. 7.1, г. Так как на частоте сопряжения асимптот выполняется условие , то частота сопряжения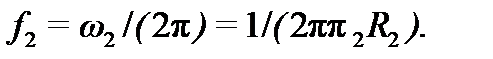

Передаточные функции приведённых простейших фильтров представляют собой уравнения первого порядка, поэтому и фильтры называются фильтрами первого порядка. Коэффициент усиления у них уменьшается с частотой на 20 дБ/дек.

При объединении фильтров низких и высоких частот (рис. 7.1,а,в) получается полосовой фильтр (рис. 7.2,а), имеющий ЛАЧХ (рис. 7.2,б).

Простейшие активные фильтры имеют малую крутизна спада ЛАЧХ, что свидетельствует о плохих избирательные свойствах. Для улучшения избирательности нужно повышать порядок передаточных функций за счёт введения дополнительных RC-фильтров. На практике наиболее часто используют ОУ с цепями ОС, работа которых описывается уравнениями второго порядка. При необходимости повысить избирательность системы отдельные фильтры второго порядка включают последовательно.

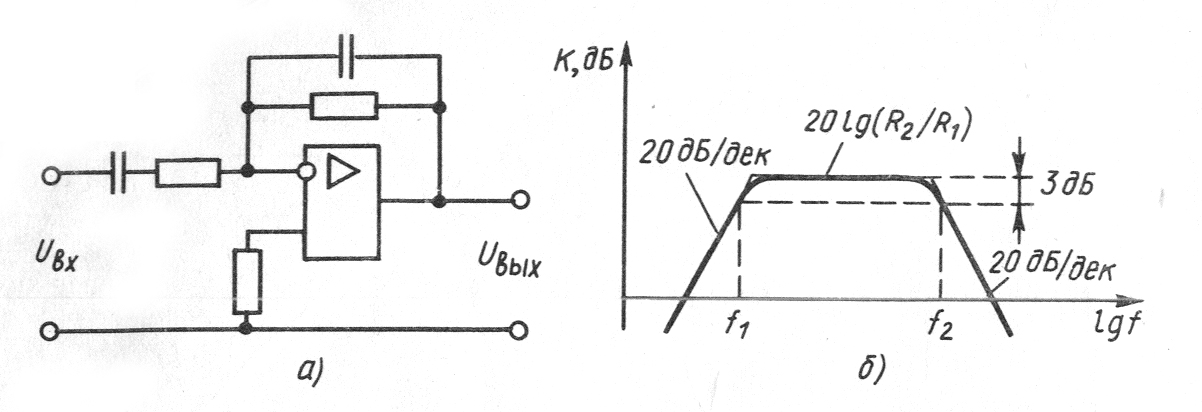
Рисунок 7.2 – Полосовой фильтр

Активные фильтры низких, высоких частот и полосовой фильтр второго порядка приведены на рис. 7.3,а,б,в. У них при соответствующем подборе номиналов резисторов и конденсаторов наклон асимптот 40 дБ/дек. Причём, как видно из рис. 7.3,а,б, переход от фильтра низких к фильтру высоких частот осуществляется заменой резисторов на конденсаторы, и наоборот. В полосовом фильтре имеются элементы фильтров низких и высоких частот.

Для полосового фильтра рис. 7.3,в резонансная частота

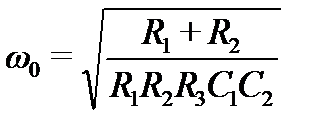
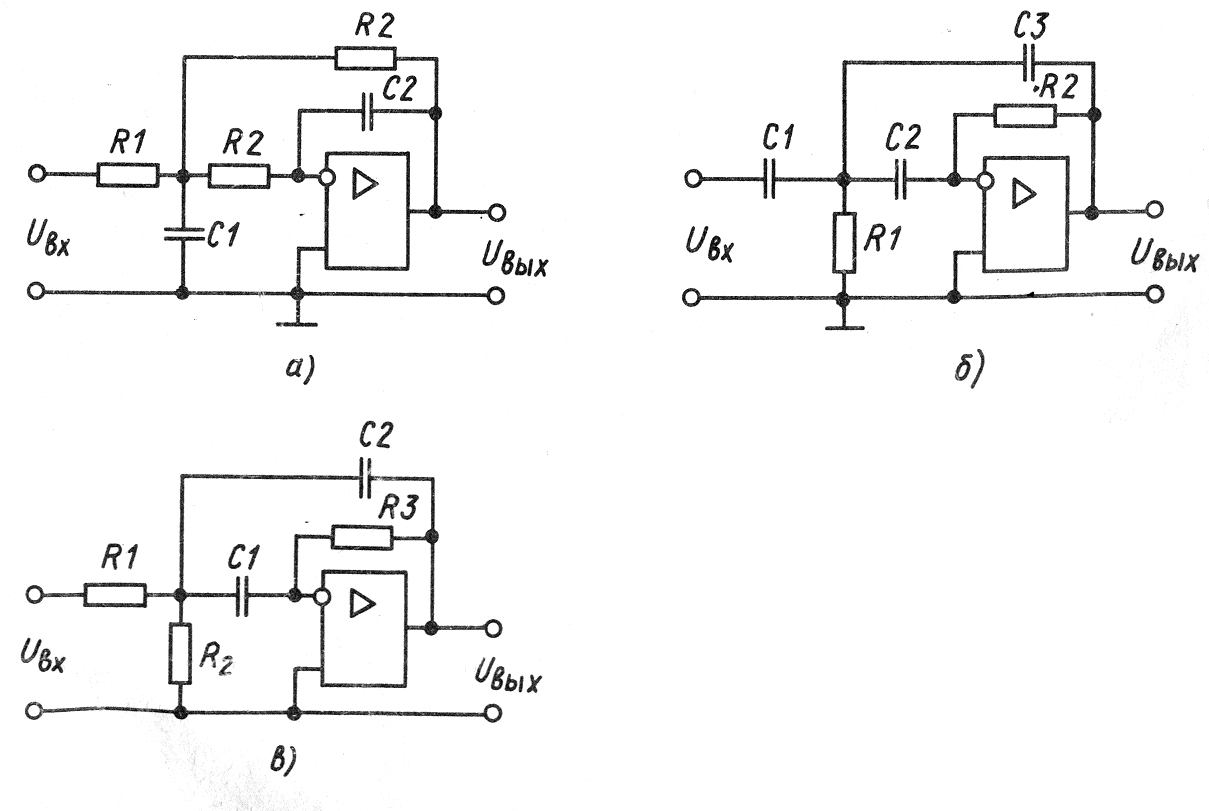
Рисунок 7.3 – Активные фильты второго порядка

Для фильтров низких и высоких частот частоты, характеризующие «начало» среза или его окончание, равны

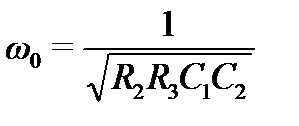
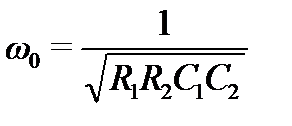
Вид их частотной характеристики зависит от параметров компонентов. Она может быть монотонно убывающей или возрастающей или иметь немонотонный вид и подъёмы вблизи частоты .

Достаточно часто полосовые фильтры второго порядка реализуют с помощью мостовых цепей. Наиболее распространены двойные Т-образные мосты, которые «не пропускают» сигнал на частоте резонанса (рис. 7.4,а) и мосты Вина, имеющие максимальный коэффициент передачи на резонансной частоте (рис. 7.4,б).

Мостовые цепи включены в цепи отрицательной и положительной ОС. В случае двойного Т - образного моста глубина отрицательной ОС минимальна на частоте резонанса. Коэффициент усиления на этой частоте имеет максимальное значение. При использовании моста Вина на частоте резонанса получается максимальная глубина положительной ОС и наибольшее усиление. При этом для сохранения устойчивости глубина отрицательной ОС, созданной с помощью резисторов R1, R2, должна быть больше положительной. Если коэффициенты положительной и отрицательной ОС близки, то данный активный фильтр может иметь эквивалентную добротность Q≈2000.

Резонансную частоту двойного Т - образного моста при 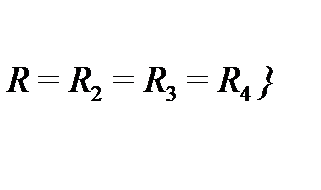и и моста Вина при и выбирают исходя из условия передачи моста Вина на частоте равен 1/3.

Для получения режекторного фильтра двойной Т- образный мост можно включить так, как показано на рис. 7.4,в, или мост Вина включить в цепь отрицательной ОС.

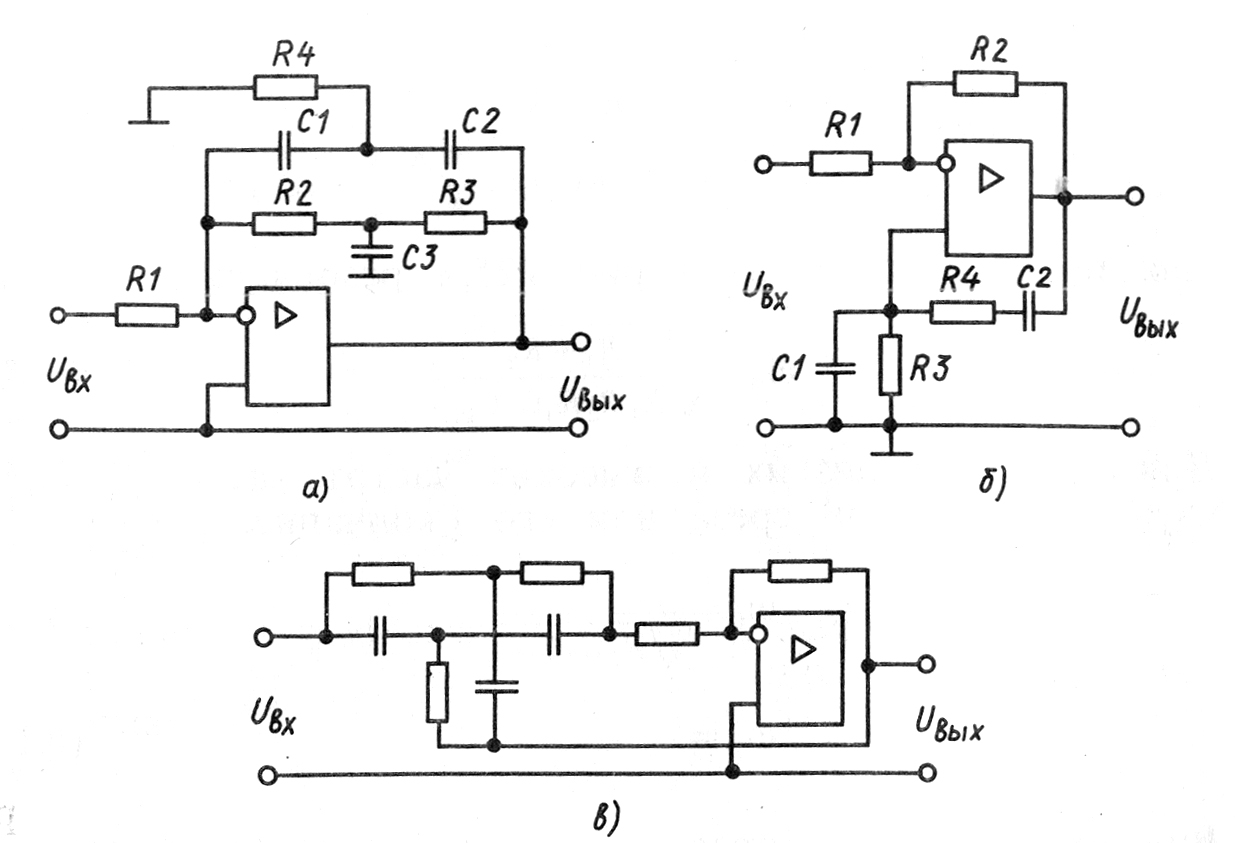
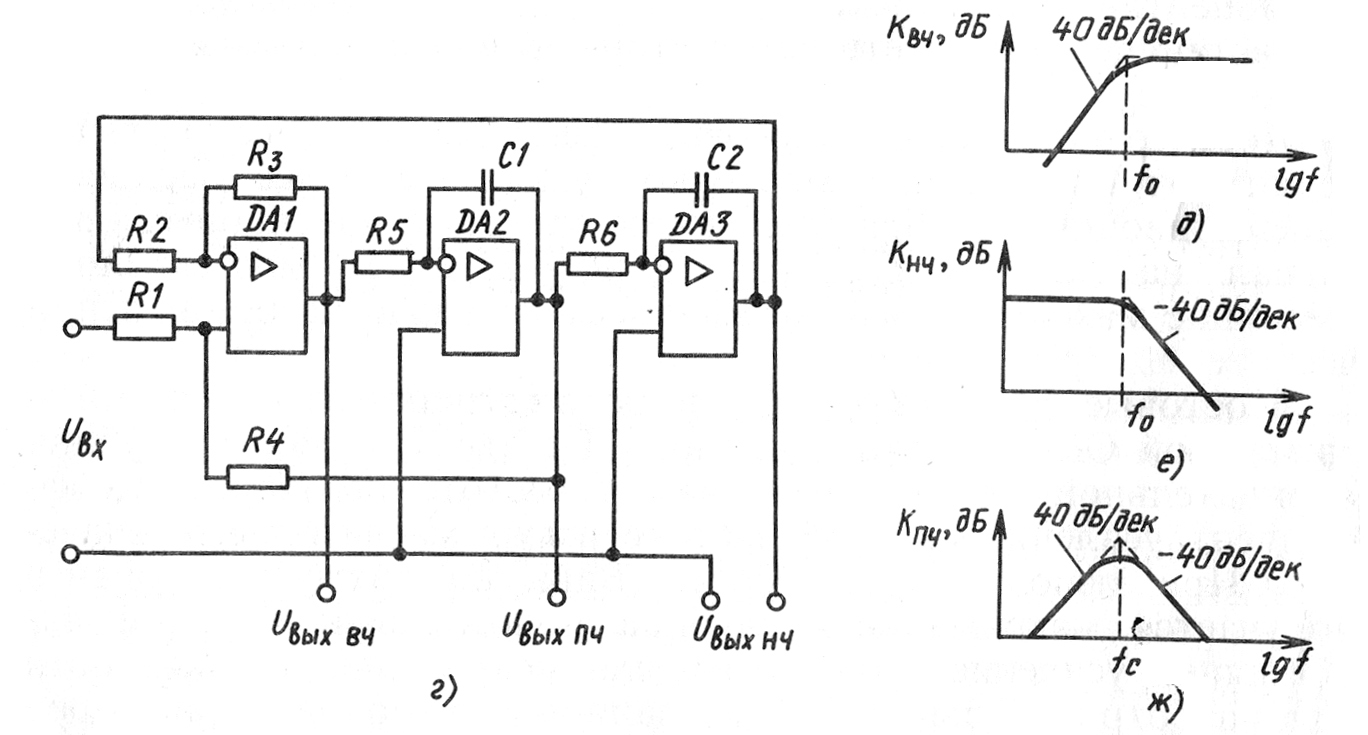
Рисунок 7.4 – Полосовые фильтры второго порядка и их характеристики

Если активный фильтр требуется перенастраивать в широких пределах, то обычно используют мост Вина, у которого резисторы и выполняют в виде сдвоенного переменного резистора.

С удешевлением и выпуском нескольких ОУ в одном корпусе начали широко применять несколько активных фильтров низких порядков, объединённых между собой в единую замкнутую систему. Пример построения такого фильтра показан на рис.7.4,г. В его состав входят сумматор на ОУ DA1 и два фильтра низких частот первого порядка на ОУ DA2, DA3. Сумматор и активные фильтры включены последовательно. Если , то частота сопряжения

Асимптоты имеют наклон 40 дБ. дек (рис. 7.4,д,е,ж). В подобном сложном фильтре удаётся одновременно реализовать фильтры низких и высоких частот, а также полосовой фильтр, который имеет сравнительно низкую чувствительность к отклонениям параметров отдельных компонентов, что бывает важно при практической реализации избирательных устройств. Структура, близкая к разобранной, использована в микросхеме типа 284CC2.

В электронных цепях кроме рассмотренных используют фазовые фильтры. Они имеют не зависящий от частоты коэффициент передачи и пропорциональный ей фазовый сдвиг выходного сигнала. В качестве фазовых фильтров можно использовать фазосдвигающие устройства (рис. 7.4,а,б), работа которых рассмотрена ранее.

Наиболее важным его параметром является групповое время задержки, под ним понимают промежуток времени, на который сигнал задерживается фазовым фильтром: . Групповое время задержки в общем случае меняется при изменении частоты сигнала и зависит от порядка уравнения, характеризующего математическую модель фильтра.

Аппроксимация характеристик активных фильтров.

Активные фильтры состоят из ОУ, работающих в линейном режиме, и пассивных элементов. Передаточные функции таких цепей представляют собой отношение двух операторных полиномов. Аппроксимация характеристик активных фильтров сводится к выбору таких коэффициентов этих полиномов, которые обеспечивают наилучшее в этом или ином смысле приближение к желаемым амплитудно-частотной (АЧХ) или фазо-частотной (ФЧХ) характеристикам фильтра.

Наиболее широко применяются следующие типы активных фильтров, отличающихся друг от друга подходом к нахождению наилучшей аппроксимации: фильтры Баттерворта, Чебышева, инверсный Чебышева, эллиптический, Бесселя.

Идеальный фильтр нижних частот (ФНЧ) пропускает с одинаковым коэффициентом (равным, например, единице) колебания, частота которых лежит в диапазоне от нуля до некоторой частоты среза . Вне этого частотного диапазона идеальный фильтр имеет коэффициент передачи, равный нулю. Однако идеальный фильтр физически нереализуем.

В фильтре Баттерворта нормированная АЧХ имеет вид

,

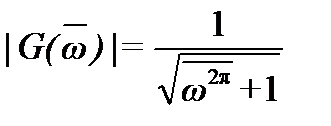Где - относительная (безразмерная) частота; -частота среза; -порядок фильтра.

Все производные функции описанной выше по частоте от первой до (2n-1)-й включительно в точке

=0 равны нулю. Поэтому фильтр Баттерворта называют фильтром с максимально плоской АЧХ.

В фильтре Чебышева аппроксимирующая функция выбирается так, чтобы в полосе пропускания фильтра получить отклонение его характеристики от идеальной, не превышающее некоторой заданной величины. За пределами же полосы пропускания фильтр должен иметь возможно меньший коэффициент передачи. При таких исходных условиях наилучшей оказывается аппроксимация вида

,

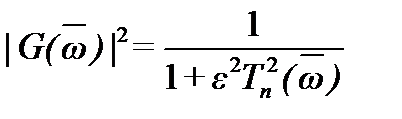где -некоторый постоянный коэффициент, определяющий неравномерность АЧХ фильтра в полосе пропускания, а – полином Чебышева первого порядка.

В полосе пропускания квадрат АЧХ 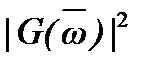фильтра Чебышева колеблется между уровнями, равными 1 и 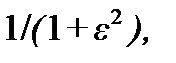причём число таких колебаний («волн» на графике АЧХ) тем больше, чем выше порядок фильтра. Поскольку амплитуда всех этих колебаний одинакова, то фильтр Чебышева называют также фильтром равных пульсаций.

В инверсном фильтре Чебышева АЧХ монотонно изменяется в полосе пропускания и пульсирует в полосе заграждения. Эта АЧХ описывается соотношением

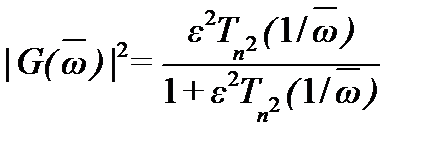
В полосе заграждения такого фильтра квадрат АЧХ 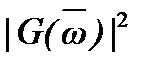пульсирует между значениями 0 и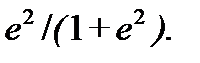

У эллиптического фильтра АЧХ характеризуется равномерными пульсациями как в полосе пропускания, так и в полосе загражления.

В фильтре Бесселя наилучшая аппроксимация ищется не для амплитудно-частотной, а для фазо-частотной характеристики фильтра. Для того чтобы фильтр не искажал сигнала, спектр которого лежит а полосе пропускания, требуется, чтобы запаздывание выходного сигнала относительно входного было одинаковым для всех гармоник. Поскольку фазовый сдвиг измеряется в долях периода рассматриваемой гармоники, то постоянство времени запаздывания равносильно линейной частотной зависимости фазового выходного сигнала относительно входного сигнала фильтра. Фильтр Бесселя обеспечивает наилучшее приближение реальной фазо-частотной характеристики к идеальной зависимости, соответствующей постоянному запаздыванию. Зависимость времени запаздывания от частоты для фильтра Бесселя имеет такой же характер, как АЧХ для фильтра Баттерворта.

На рис. 7.5 показаны примеры АЧХ фильтров 4-го порядка различных типов. Фильтр Чебышева и эллиптический фильтр в данном случае характеризуются пульсациями в полосе пропускания, размах которых равен 0,5 дБ, а инверсный фильтр Чебышева и

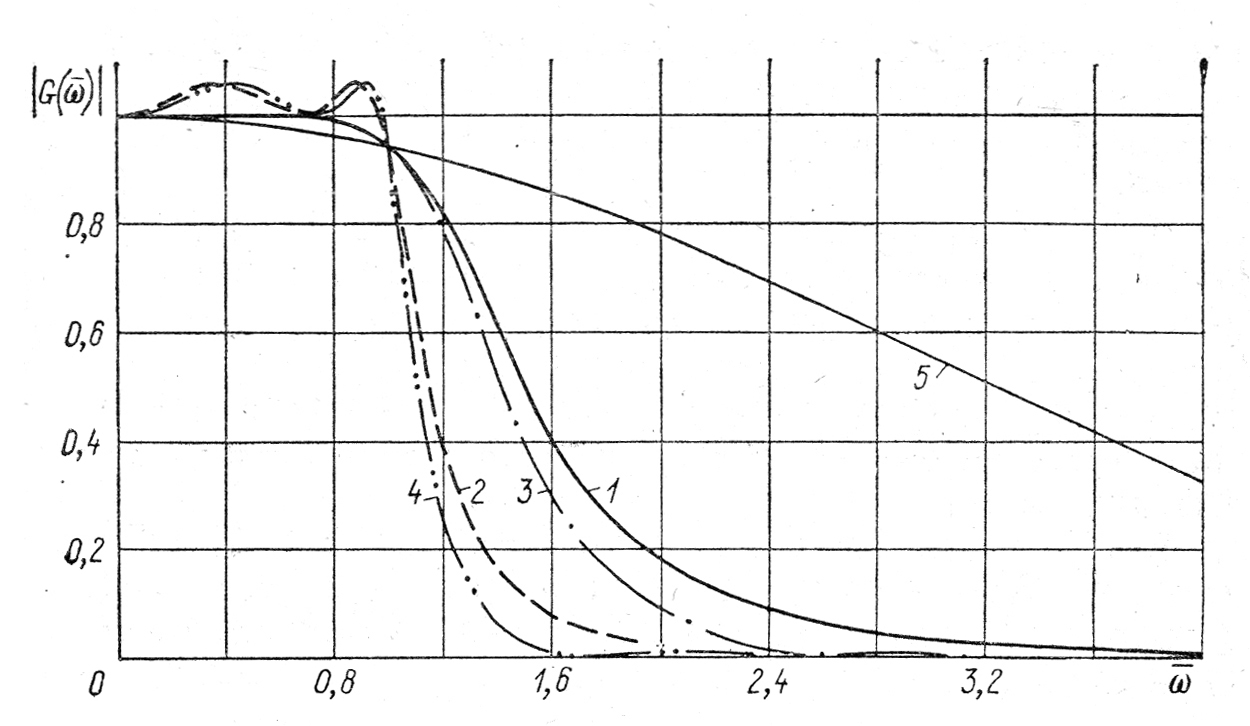
Рисунок 7.5 – Амплитудно-частотные характеристики фильтров 4-го порядка

эллиптический фильтр имеют в полосе заграждения пульсации, вершины которых лежат на уровне -40 дБ. Для всех фильтров выбрана одинаковая частота среза =1 при спаде АЧХ, равном 0,5 дБ.

Из рис. 7.5 видно, что наибольшую скорость спада АЧХ в переходной области (между полосами пропускания и заграждения) имеет эллиптический фильтр. Далее следуют фильтры Чебышева, инверсные Чебышева и Баттерворта. Наихудшим в этом смысле является фильтр Бесселя. Однако при скачке входного сигнала выходное напряжение фильтра Бесселя устанавливается наиболее быстро, а у эллиптического фильтра и фильтра Чебышева – наиболее медленно.

Для воспроизведения передаточных функций можно использовать соединённые последовательно звенья 2-го порядка. Чаще других для реализации активных фильтров применяют звенья, схемы которых показаны на рис7.6 и 7.7.

Звено по схеме рис.7.6,а построено на основе неинвертирующего усилителя или, как его называют в теории активных фильтров, источника напряжения, управляемого напряжением (ещё одно название – структура Сален -Ки). Для этой цепи передаточная функция имеет вид

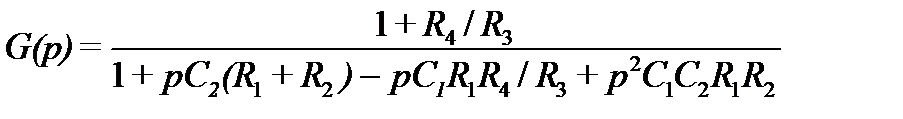
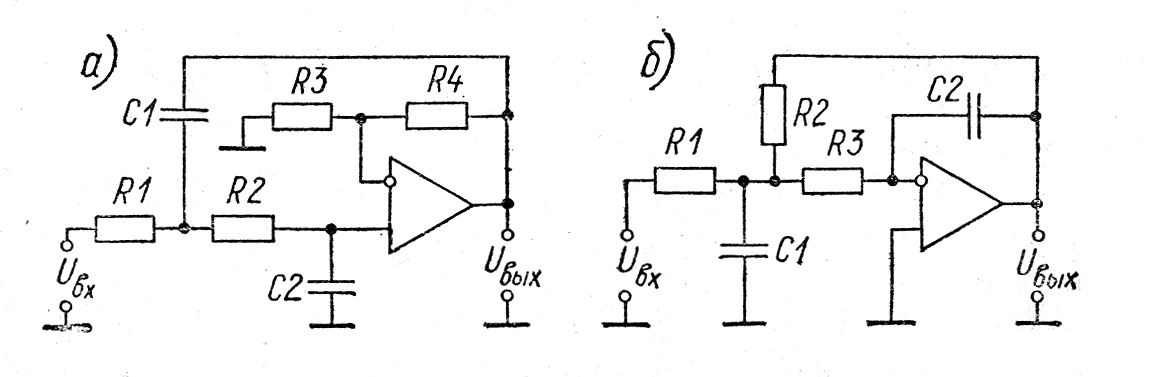
Рисунок 7.6 – Фильтр 2-го порядка на основе неинвертирующего усилителя.

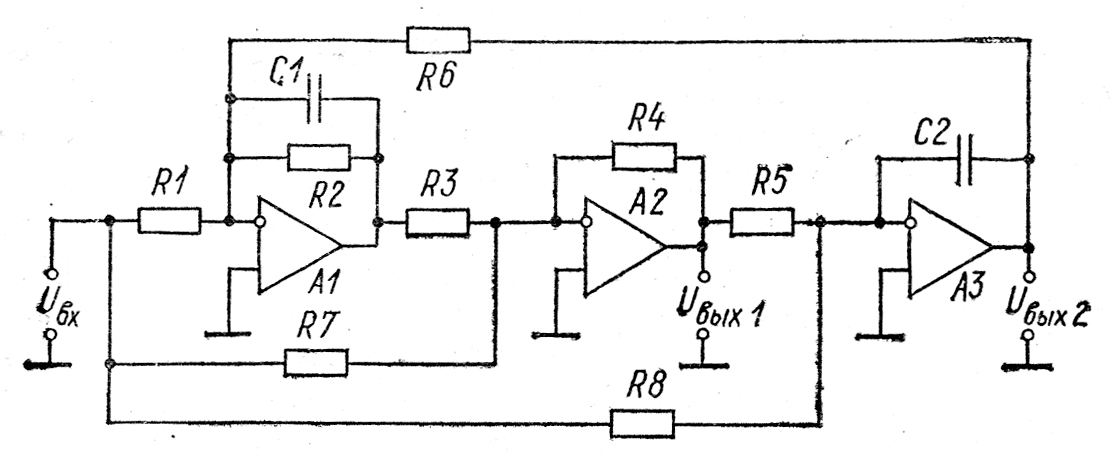
Рисунок 7.7 – Схема универсального фильтра с биквадратным звеном

Звено по схеме рис.7.6,б называют звеном с многопетлёвой обратной связью или структурой Рауха. Для него

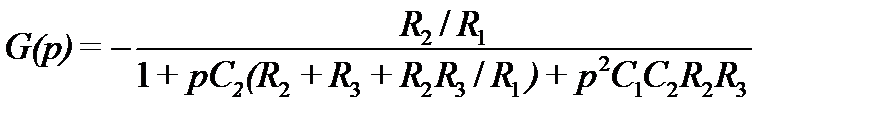
Звенья, показанные на рис. 7.6, пригодны для реализации только полиномиальных фильтров (Баттерворта, Чебышева и Бесселя). Более универсальным, хотя и более сложным, является биквадратное звено, схема которого показана на рис.7.7. Для него можно найти

Если принять , то можно использовать как выходное напряжение звена эллиптического фильтра или инверсного фильтра Чебышева. Если же R7= и R8= , то выходное напряжение соответствует звену 2-го порядка фильтров Баттерворта, Чебышева и Бесселя. Биквадратное звено (рис. 7.7) менее чувствительно, чем звенья по схеме рис. 7.6, к неточности элементов и проще в настройке.

Нетрудно вывести формулы для расчёта сопротивлений и ёмкостей выбранных звеньев 2-го порядка.

Рекомендуется следующий порядок расчёта ФНЧ. Исходно задаются частота среза фильтра 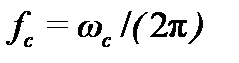и коэффициент усиления звена в полосе пропускания А. Расчёт во всех случаях начинают с выбора ёмкости . Для того чтобы получить приемлемые сопротивления резисторов, рекомендуется выбирать примерно равной 10/ (мкФ), где – частота реза в герцах.

При использовании схемы рис. 7.6,а вначале определяют , и ( значения a, b, c берут из таблиц:

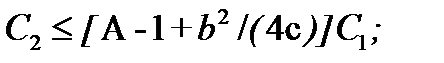
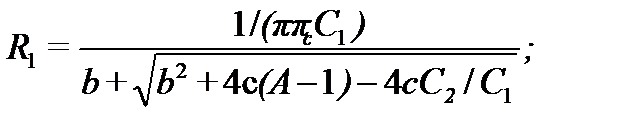
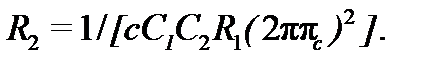
Наконец, исходя из заданного коэффициента усиления А находят сопротивления и . Если А=1. то R3= 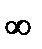, R4=0. Если А>1, то, исходя из равенства сопротивлений для входных токов И- и Н- входов ОУ, нетрудно получить соотношения

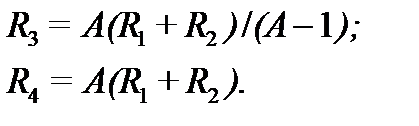
Для схемы рис. 7.6,б расчёт также начинают с выбора ёмкости (мкФ), где – частота среза, Гц. Далее используют формулы:

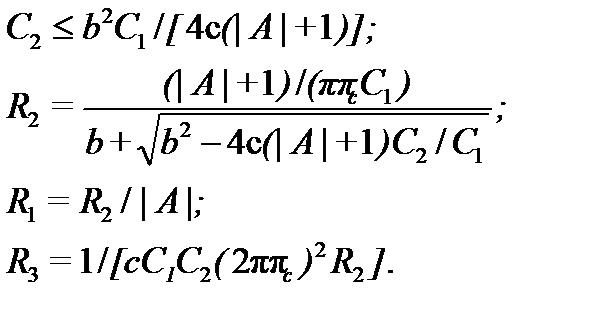
Для биквадратного звена полиномиального фильтра (рис. 7.7) выходным является напряжение ; при этом , целесообразное значение находят также, как и в предыдущих случаях, а затем определяют остальные элементы:

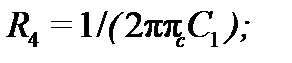
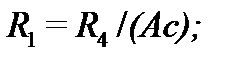
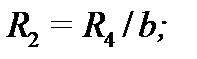
Биквадратное звено неполиномиальных фильтров (рис. 7.7, ) рассчитывают, пользуясь соотношениями:

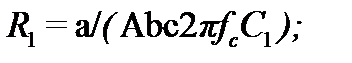
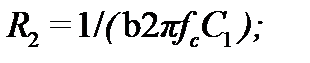
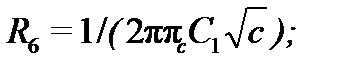
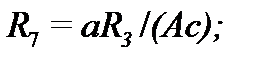
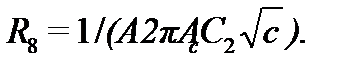
При этом целесообразное значение ёмкости выбирают так же, как и раньше ( , где в микрофардах, а в герцах), а и выбирают так, чтобы уменьшить разброс получаемых в результате расчёта сопротивлений. Для большинства случаев можно принимать = и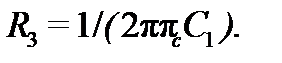

Передаточные функции фильтров верхних частот можно получить, вместо p подставить . При этом для неполиномиальных фильтров характер передаточной функции сохраняется, изменяются только её коэффициенты. Это значит, что неполиномиальные фильтры верхних частот реализуют с помощью точно таких же схем, как и фильтры нижних частот, но при других сопротивлениях и ёмкостях. Для полиномиальных фильтров передаточные функции для ФНЧ и ФВЧ различаются по своему характеру. Во всех случаях коэффициенты передаточных функций ФВЧ могут быть рассчитаны, исходя из данных, приведённых в табл.1, и заданной частоты среза

Звенья второго порядка, пригодные для реализации полиномиальных фильтров верхних частот, легко получить, исходя из соответствующих звеньев фильтров нижних частот. При этом в схеме рис. 3.1,а резисторы , заменяются на конденсаторы, а конденсаторы , – на резисторы. В схеме рис. 225,б аналогично резисторы , , заменяются конденсаторами, а конденсаторы , – резисторами.

В схеме рис. 7.7 в качестве выходного напряжения звена полиномиального ФВЧ следует использовать напряжение Uвых1, при этом нужно принять R8=оо и выполнить условие .

Задание на самостоятельную работу:

1. Какие основные характеристики определяют фильтр?

2. Выполнить схему фильтра нижних частот.

3. Выполнить схему фильтра верхних частот.

4. Выполнить схему полосового фильтра.